This project is aimed at creating an algorithm that optimizes subway headway by running multiple simulations and using graphical analysis on the data points gather from the simulations to determine the most efficient headway. The simulation is able to find the most efficient headway by balancing total minutes waited and amount of trains used in the system, using this to calculate the headway that balances both.

Abstract

Graphical abstract

Subway systems are the backbone of many large cities worldwide, however with an increase in urban population this means subway systems are under more stress than ever (Gentile, 2015). This compounded with city transit budgets being stressed introduces a challenge for stretching the resources a system has to its maximum. This paper presents a novel approach to generate optimal train schedules for subway systems using a generalized formula for minimizing both passenger wait times and city funds. A series of smaller subway systems are designed to test different configurations and scenarios. These systems are then stress tested under a variety of headway times with both the total time in minutes waited by all passengers at each station and the amount of trains used to make the headway possible (Peng et al., 2025). This data is collected and the relationship between the variables is noted. These variable relationships are used to form a series of equations describing the headway, with different equations focusing on different aspects of the system and the headway (Singhania & Marinov, 2017). A gradient descent procedure is then applied to these equations to form a series of parameters that can be applied to all subways to optimize headways. This will provide accurate data to decrease passenger wait times and save city funds across all subway systems.

Proposal link

Engineering need

Engineering goal

Subway systems are the backbone for many cities and thus it's important for subways to be optimized so they can allocate city funds by minimizing trains and minimizing rider wait times.

The goal was to create an algorithm by simulating subway systems and using the data points generated from these simulations to balance both the amount of trains and total time waited by using a headway that balances both.

Background

This project develops a subway system simulation to optimize headway—the time interval between trains—by minimizing both the number of trains used and passenger wait times. The goal is to create a general set of equations applicable to any subway system. Effective headway management is crucial for urban transit systems, as overcrowding and resource misallocation lead to delays and inefficiencies. For example, in 2022, an estimated 36.7 million hours were wasted in New York City due to suboptimal subway performance (NYC Transit, 2022). Optimizing headways can address these issues, balancing city resource allocation and passenger needs. Current studies often focus on average travel time or shortest path as optimization metrics (Assis & Milani, 2004; Gentile, 2015; Peng et al., 2025). However, these approaches can result in irregular headways for less busy stations, skewing results (Özgür Yalçınkaya & Bayhan, 2009; Yildirim & Aydın, 2022). This study instead uses total wait time, providing a more comprehensive system evaluation. Additionally, resource management, specifically the number of trains on a line, is considered—a factor often overlooked in other studies (Li & Zhou, 2019; Gentile, 2017; Zang et al, 2020). Optimizing train usage ensures practical applications and realistic solutions. Testing subway optimization in real-world scenarios is challenging due to the reliance of millions on these systems. Instead, simulation models are employed, allowing data collection and analysis without disrupting operations (Singhania & Marinov, 2017). Gradient descent is used to identify optimal patterns, such as the ideal headway balancing wait times and train usage. This analysis forms the basis for generalized equations applicable to subway systems globally. By focusing on often-overlooked metrics like total wait time and train allocation, this project aims to improve subway efficiency and affordability worldwide through simulation and gradient descent optimization.

Procedure

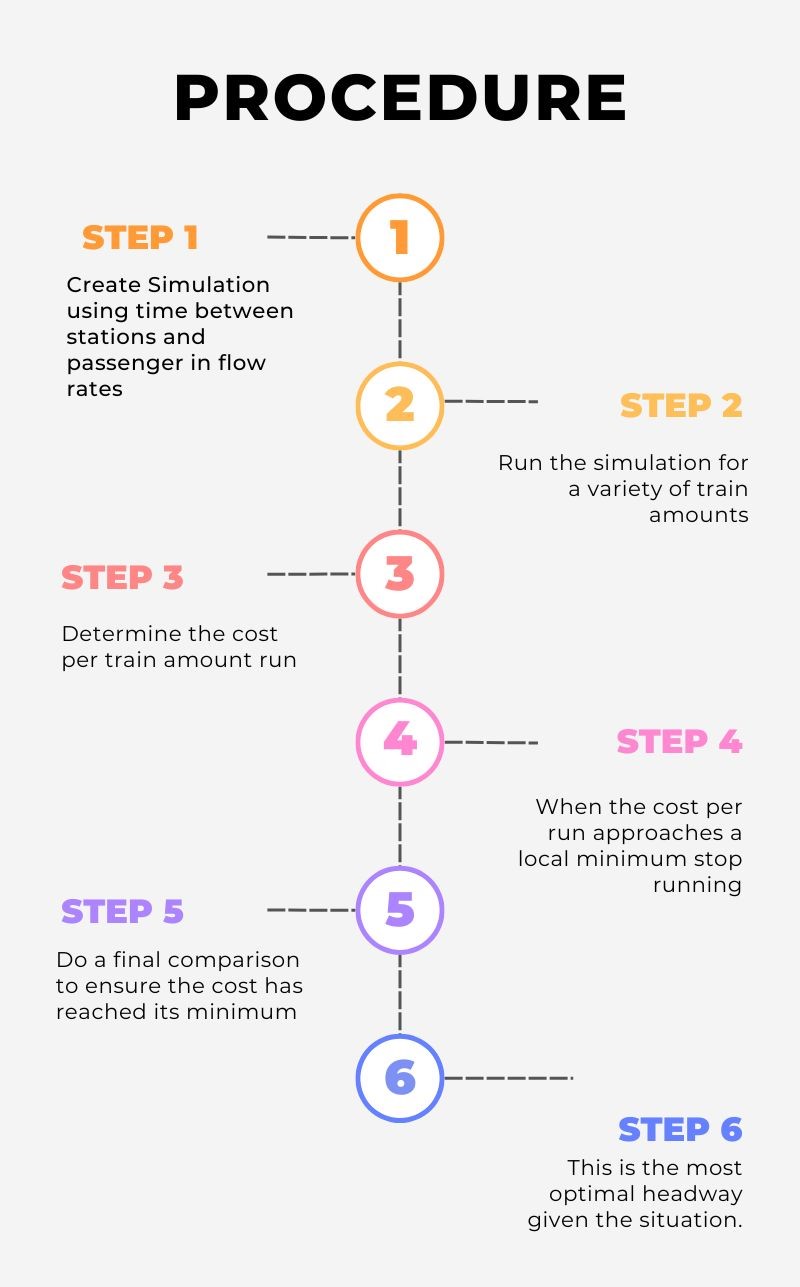
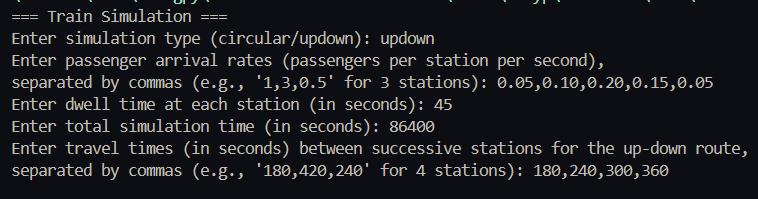
The procedure for this study involved the development of a subway simulation built in python that used the time between stations and the passenger inflow rate per station. From there it tested a variety of train amounts and through simulation determined the total wait time, all over a 24 hour period. The simulation had several loops, each representing a real world second where passengers board trains or accumulate at stations and at the end the amount of passengers waiting gets accounted for by the system. It then determines the cost by using the total amount of waiting time and trains used, and then from there the cost was calculated per train amount. Gradient descent is then applied on the data and cost equations, and stops simulating when the local minimum is found. This systematic approach allows for optimized headways to be found by minimizing cost, which are specialized for each subway system.

Results

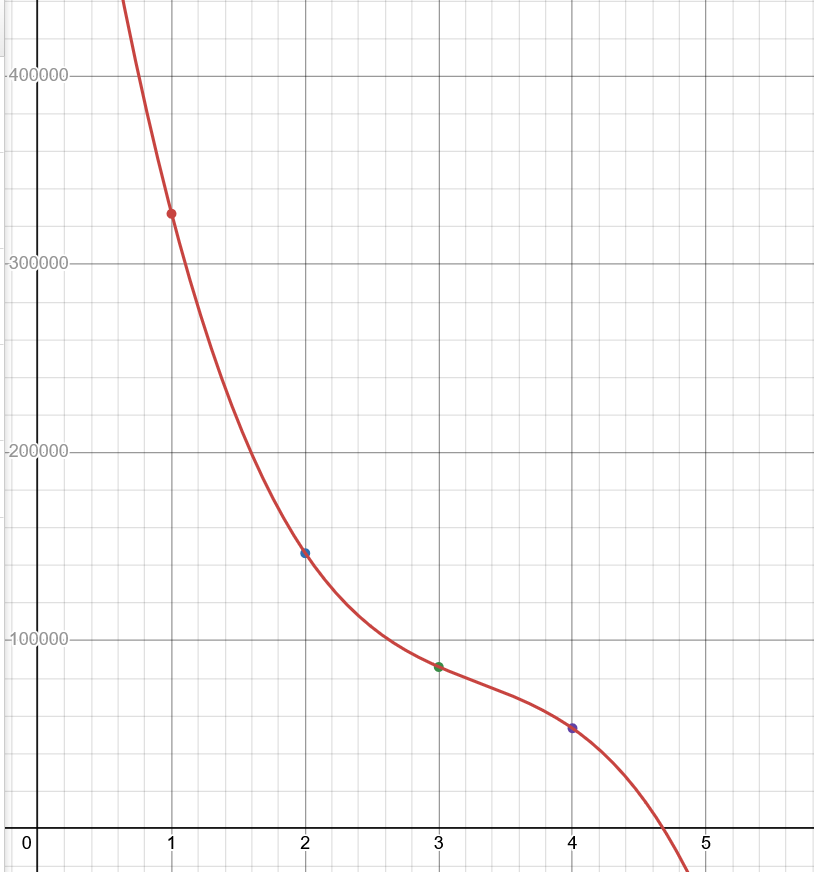
Line of best fit for the given data points, showing cost as amount of trains increased

Data points for an example system of 4 stations on a loop

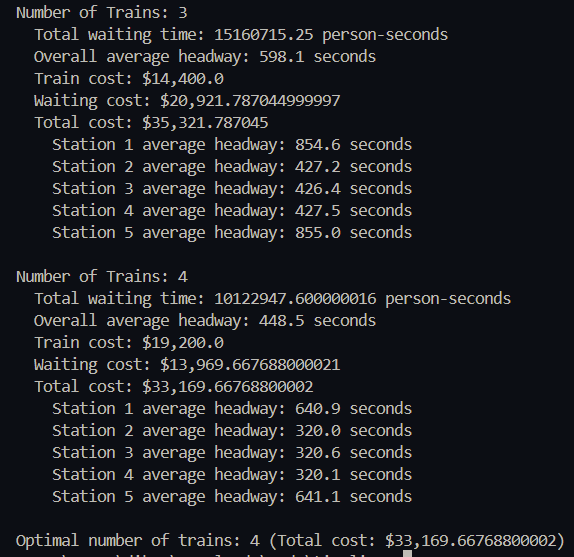
Data points representing the Cambridge portion of the MBTA red line.

Number of trains compared to 4 trains for this given system portion, showing the cost reaches the minimum at 4 trains.

Analysis

Based on the simulation we can see that there is a clear trend whereas more trains are added to the given system, their worth in terms of decreasing time-waited lowers. We can then use this data to run a gradient descent algorithm to determine at what point is the optimal for balancing the number of trains and the total minutes waited. While only one example was used here, this graph can be generated for any given subway system and would allow for optimization across the world.

Discussion

The data collected from the simulations reveal a clear relationship between headway times, passenger waiting times, and the number of trains used. The gradient decent analysis successfully identified which headway configurations were the most optimal. The headways that minimized both total passengers’ wait times and number of trains required were identified and once identified it was clear that they came into similar regions of the graph. These findings align with the project’s objectives and show that a balance between resource efficiency and passenger satisfaction exists and is feasible to achieve. This study differs from previous research similar to Gentile (2015) and Zang et al. (2020), which focused primarily on average wait times and shortest path optimizations. This project alternatively focuses on total so as to not obscure outliers in the data. Similar to (Yildirim & Aydın, 2022) the study leverages simulation models and gradient descent to use generalized equations for specific situations. The findings of this study has significant implications for urban transit worldwide, it can reduce passenger wait times and better city fund allocations.

References