An Analytical and Numerical Study of Dynamic Materials

Suzanne L. Weekes & Konstantin A. Lurie
Department of Mathematical Sciences
Worcester Polytechnic Institute
Worcester, Massachussetts, 01609


We work in the novel paradigm of spatio-temporal composites or dynamic materials. These are formations assembled from materials which are distributed on a microscale in space and in time. This material concept takes into consideration inertial, elastic, electromagnetic and other material properties that affect the dynamic behavior of various mechanical, electrical and environmental systems. In static or non-smart applications, the design variables, such as material density and stiffness, yield force and other structural parameters are position dependent but invariant in time. When it comes to dynamic applications, we also need temporal variability in the material properties in order to adequately match the changing environment. To this end, in dynamic material design, dynamic materials will take up the role played by ordinary composites in static material design. A dynamic disturbance on a scale much greater than the scale of a spatio-temporal microstructure will perceive this formation as a new material with its own effective properties.

By allowing spatio-temporal variability in the material constituents, we can create effects that are unachievable through purely spatial design. For example, by appropriately controlling the design factors of a dynamic composite, it is possible to selectively screen large domains in space-time from the invasion of long wave disturbances. One is also able to eliminate the cut-off frequency phenomenon in electromagnetic waveguides; and, dynamic materials may also act towards more effective high frequency power amplification and generation implemented through wave coupling.

Mathematically, the problem is formulated for linear, hyperbolic equations with spatio-temporally varying senior coefficients. Both analytic and computational means are applied to the analysis of the effective properties of dynamic materials generated by various microstructures in two or three spatial dimensions and time. Analytically, by applying homogenization, it will be possible to specify attainable bounds for such parameters related to the binary mixtures of isotropic dielectrics in the framework of Maxwell's theory. Computationally, direct numerical simulation of the original equations will be performed to understand the physics of wave propagation through heterogeneous media with complex microstructure. Together, both approaches will lead to the correct formulation and analysis of optimal material design in space-time in response to a dynamic environment.

This material is based upon work supported by the National Science Foundation under DMS grant 0204673.

Book - "An Introduction to the Mathematical Theory of Dynamic Materials" by Konstantin A. Lurie, Advances in Mechanics and Materials, Volume 15, 2007

Some Related Papers Consider the longitudinal vibration of an infinite elastic bar,
(rho z_t)_t - (k z_x)_x = 0,
where density and stiffness are denoted repectively by rho and k ; or an electromagnetic material, composed of isotropic dielectrics, with permittivity and permeability denoted by epsilon and mu ,
(epsilon z_t)_t - ((1/mu) z_x)_x = 0.
Assume that the material parameters are specified as fast, periodic functions of both time t and space x . More precisely, assume that at an initial instant, t = 0, the property pattern is defined as a periodic array of segments of length d such that
(rho1, k1) - "material 1" occupies volume fraction m
and
(rho2, k2) - "material 2" occupies the volume fraction 1-m

For t > 0 , the array moves along the x-axis with a uniform speed V . The material parameters (rho, k) thus become periodic functions of the argument (x-Vt)/e where e is a small parameter.

This material pattern may be characterized as a laminate in space-time. Such characterization does not imply, however, any actual material motion: the material itself remains motionless, whereas its property pattern is exposed to the uniform movement along the bar.

The long wave dynamic disturbances will perceive this formation as a new effective medium having no dispersion and moving with some background speed.
Like its uniform material counterpart, this material will allow D'Alembert waves travelling with some characteristic phase velocities.
Under a special choice of parameters for the density and stiffness rho and k , these waves may travel in the same direction.
This page contains some numerical computations which illustrate this coordinated wave motion.

In the following:
V is laminate velocity
a1 is char. speed of material 1
a2 is char. speed of material 2
s1, s2 are the effective velocities
mp is proportion of material 1 in laminate

COORDINATED WAVE MOTION IN A DYNAMIC LAMINATE

Consider a one-dimensional material subject to space-time lamination of rho and k .
For this example, we use (k1,rho1) = (1,1); (k2,rho2) = (10,9); mp = 0.5
For coordinated wave motion yielding a "screening effect", choose V such that
0.60302269 < V < 1 or -1.0 < V < -0.60302269.

Click to enlarge plots
V = 0.8;
Initial data z=e^(-5x^2), z_t = 0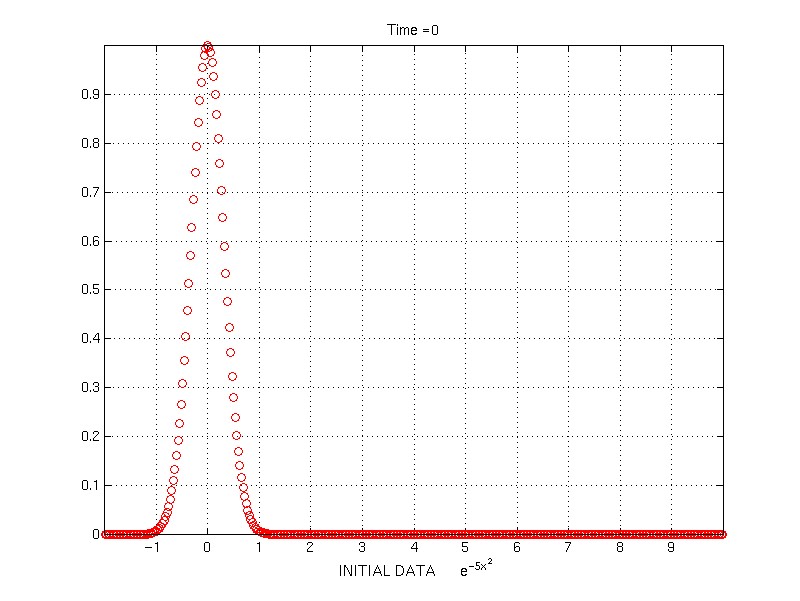
Initial Data e^(-5x^2) 		Time = 3.001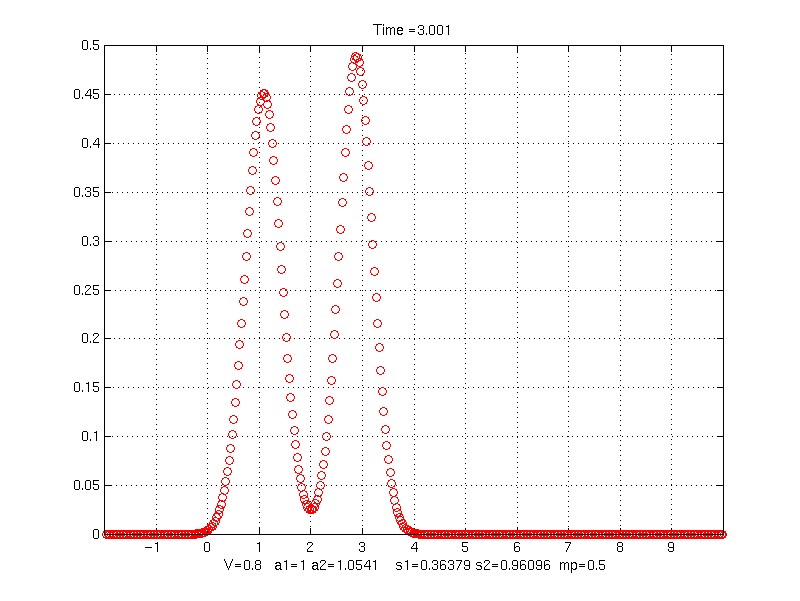
Time 3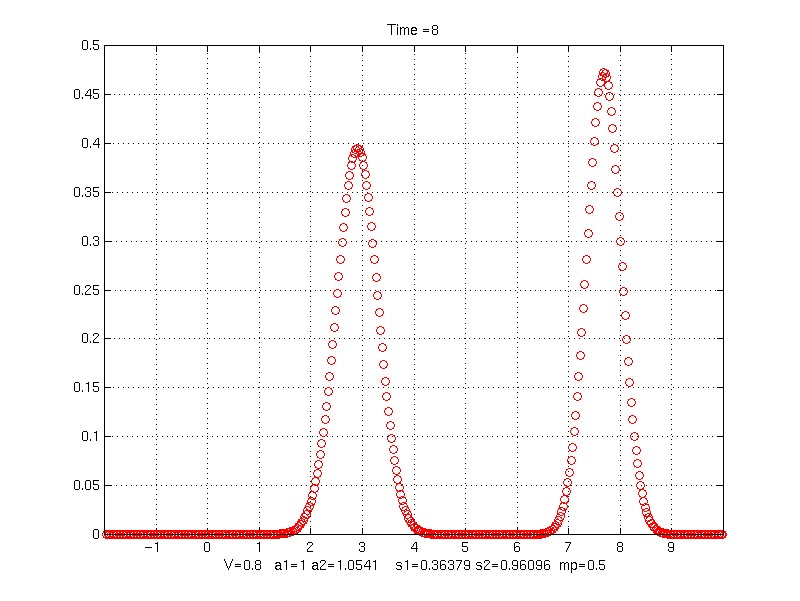
Time = 8
Time 8 		Contour plot of evolution of profile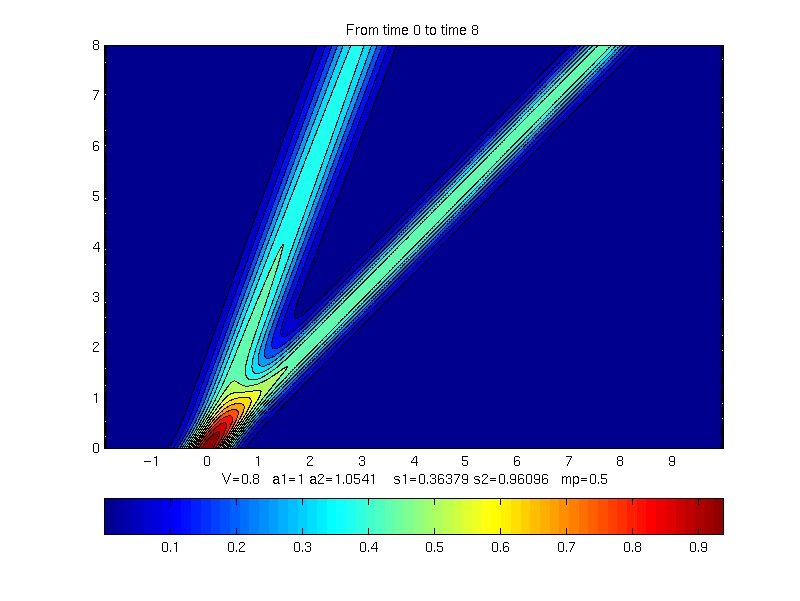
Contour_08

s1 = 0.36378913 s2 = 0.96095791
V = -0.8;
Time = 8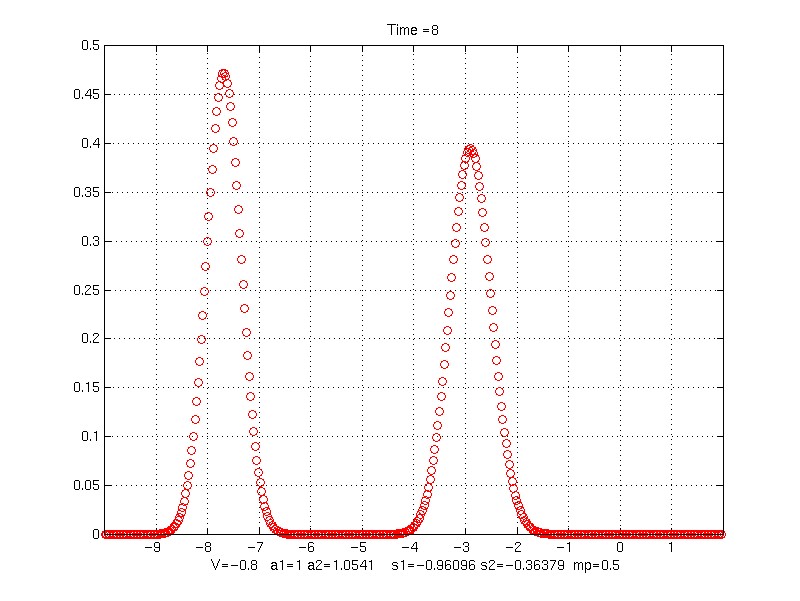
Time 8 		Contour plot of evolution of profile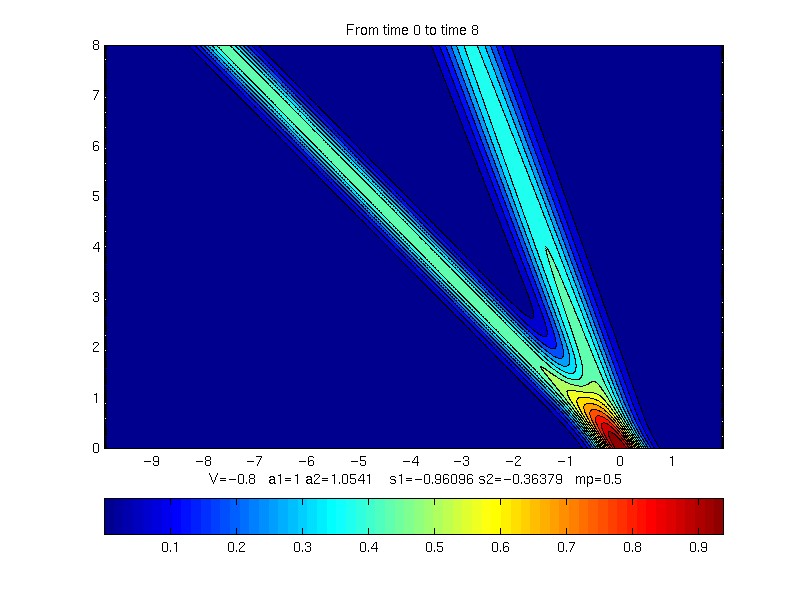
Contour_n08

s1 = 0.36378913 s2 = 0.96095791
V = 0.3;
Time = 5
Time 5 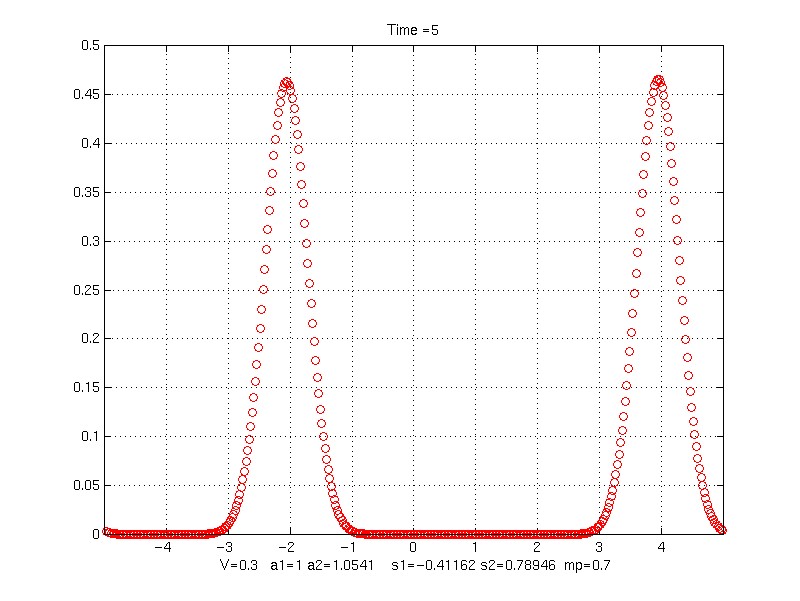		Contour plot of evolution of profile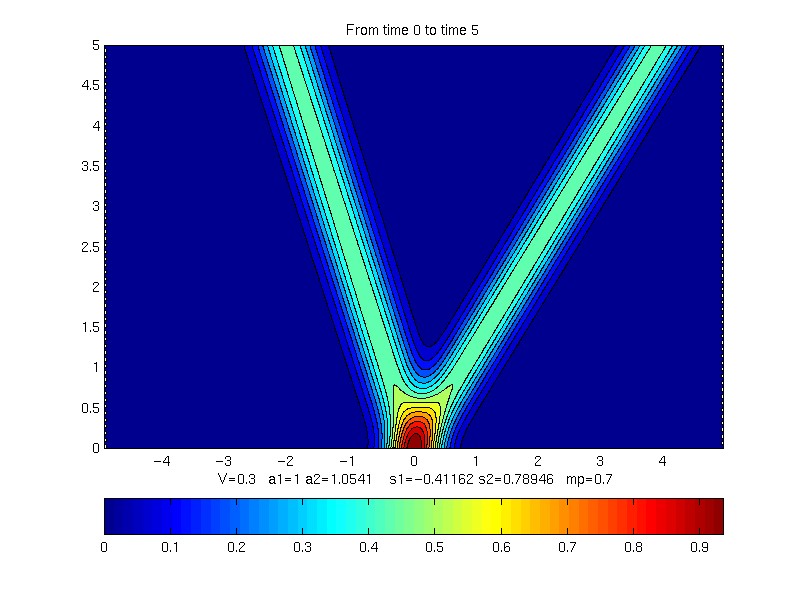
Contour_03

s1 = -0.41161806 s2 = 0.78946064

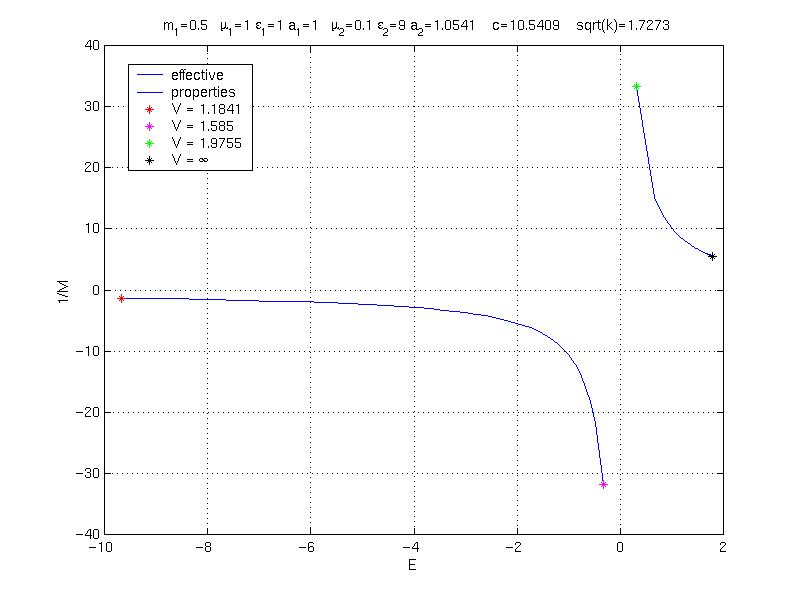
EFFECTIVE PROPERTIES IN ELECTROMAGNETIC MATERIALS

Effective Properties
Click to enlarge plot

Consider a laminate assembled from two isotropic dielectrics with the property pattern moving with velocity V .
In response to long wave disturbances, the heterogeneous material acts as a uniform medium characterized by its effective permittivity E , and effective permeability M .
This figure is a plot of 1/M versus E , with V varying along the curve.
Note that the parameters of the problem can be chosen so that the effective properties are negative!


EFFECT OF LAYER WIDTH ON SOLUTION:

k1 = 1, k2 = 10, rho1 = 1, rho1 = 2.5, mp = 0.5, V = 0.0;
s1 = -1.01929438 s2 = 1.01929438
to Time = 3.0;

20 property pair layers (40 grid points/layer)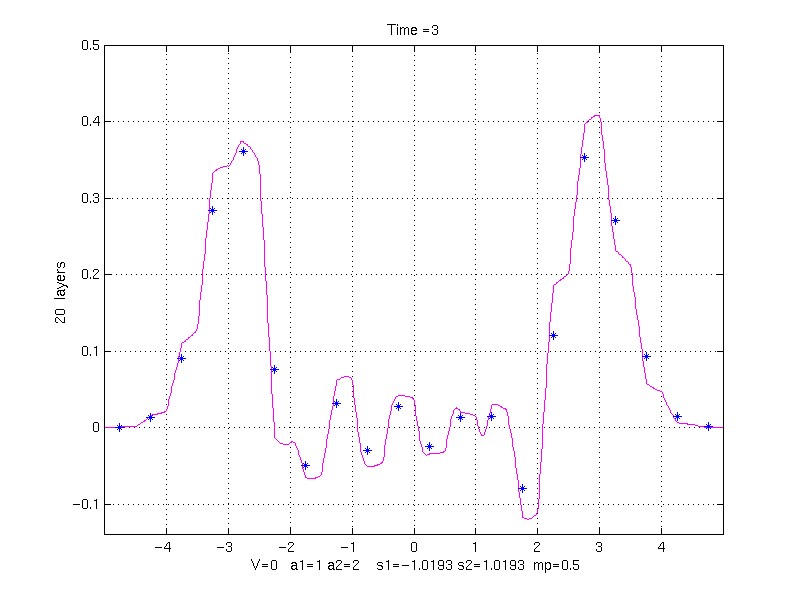
20 Layers 		40 property pair layers (20 grid points/layer)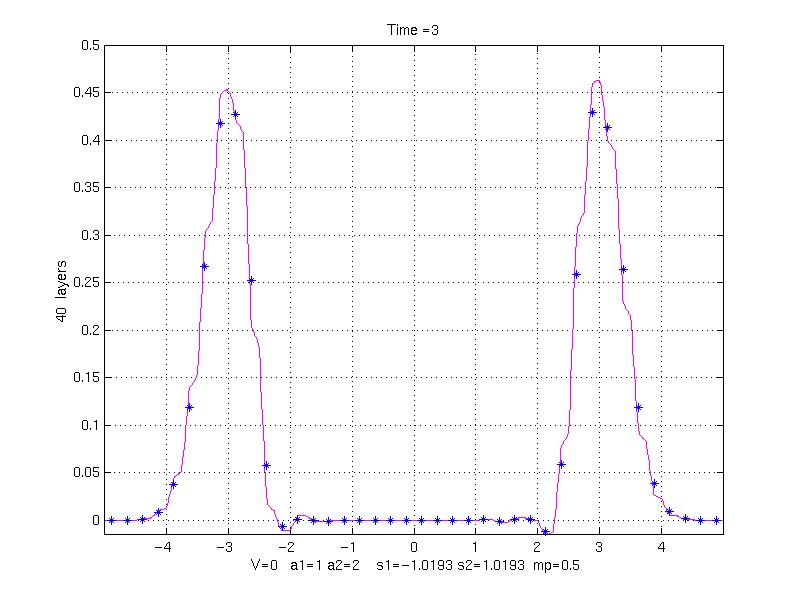
40 Layers
100 property pair layers (8 grid points/layer)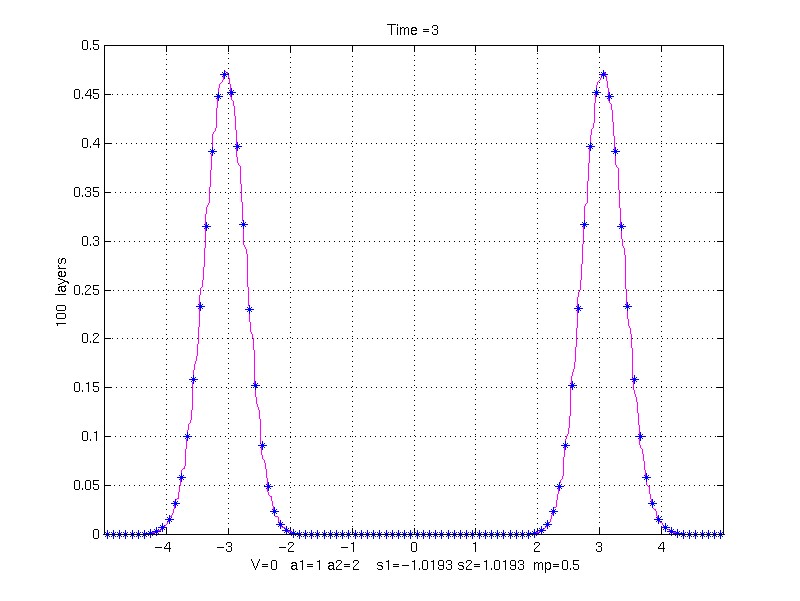
100 Layers 		200 property pair layers (4 grid points/layer)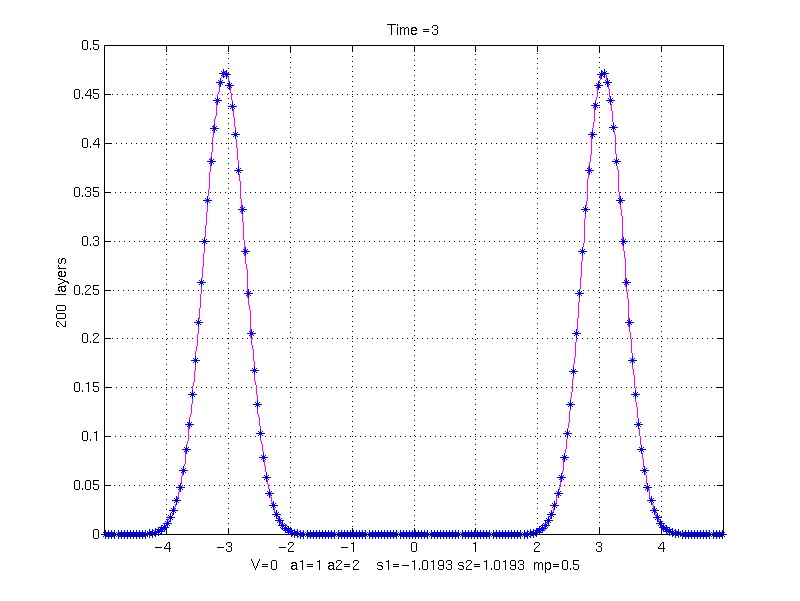
200 Layers


k1 = 1, k2 = 10, rho1 = 1, rho1 = 9, mp = 0.5, V = 0.8;
s1 = 0.36378913 s2 = 0.96095791
to Time = 8.0
20 property pair layers (40 grid points/layer)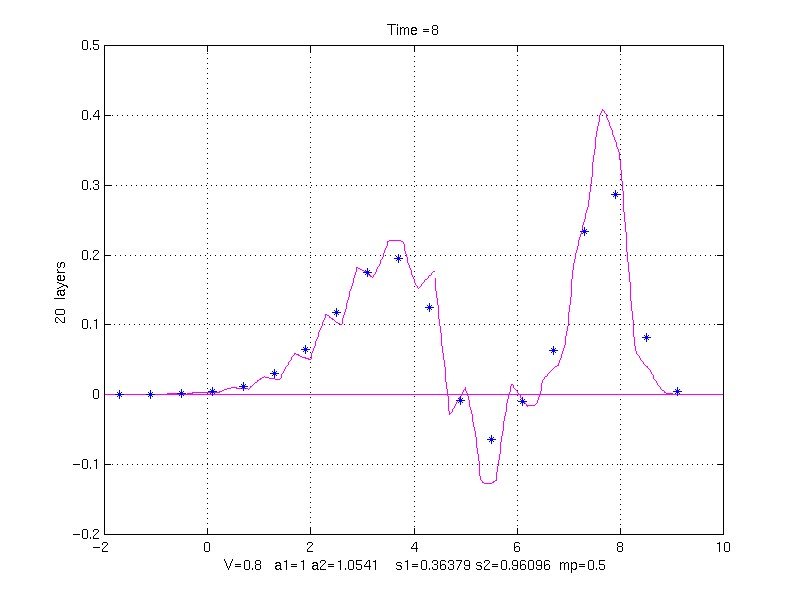
20 Layers 		40 property pair layers (20 grid points/layer)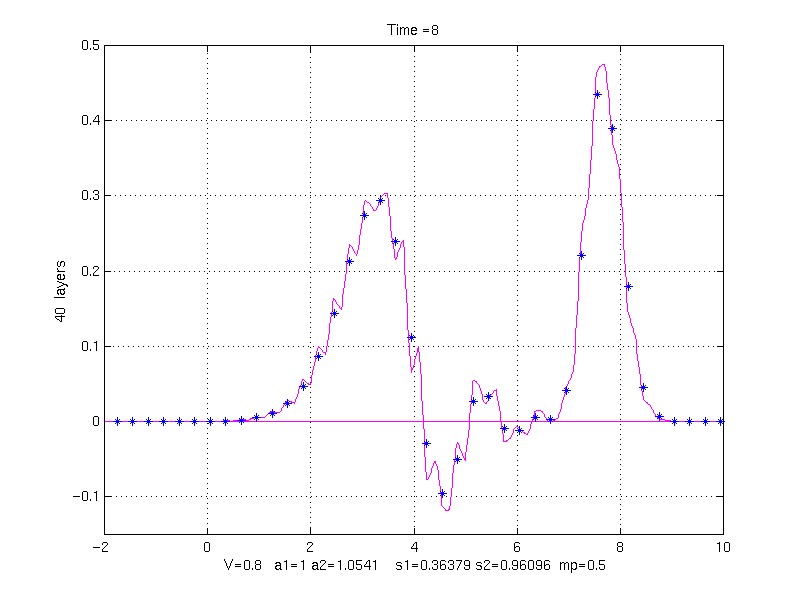
40 Layers
100 property pair layers (8 grid points/layer)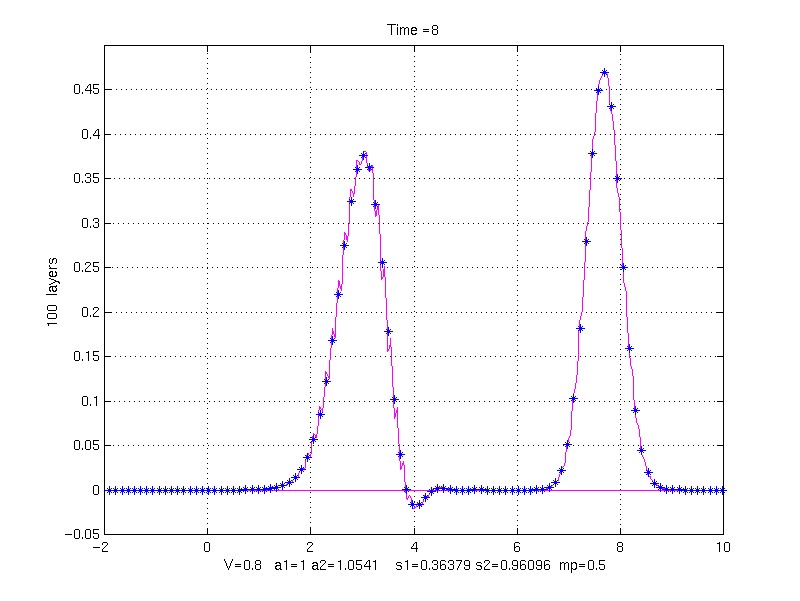
100 Layers 		200 property pair layers (4 grid points/layer)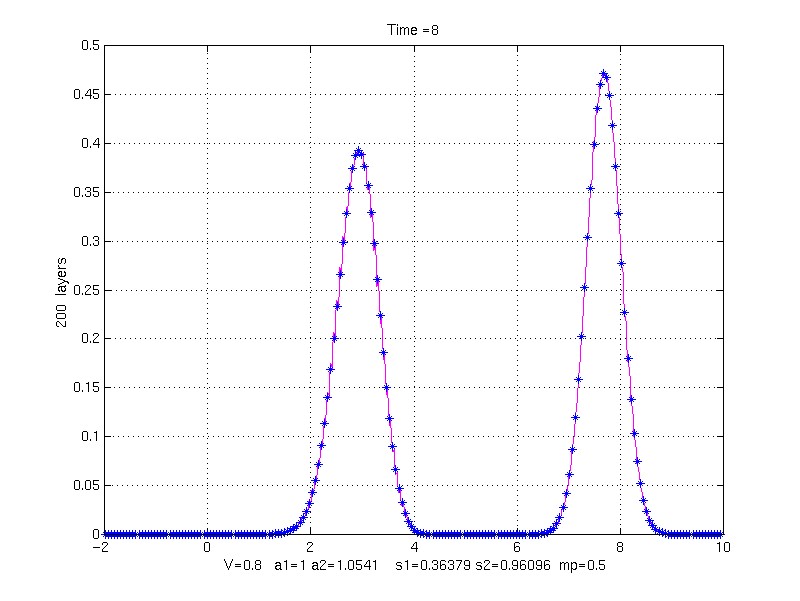
200 Layers