|
Linear Algebra
I Section E01, E'00 |
MINI PROJECT |
Back to
|
|---|
| 5. Systems of Linear Differential Equations |
|---|
|
Linear Algebra
I Section E01, E'00 |
MINI PROJECT |
Back to
|
|---|
| 5. Systems of Linear Differential Equations |
|---|
Eigenvalues play important role in the solution of systems of linear differential equation. The present Introduction reminds you some key steps of the procedure of the solution of systems of linear DE with constant coefficients.
The system of 1st order equations can be represented in the form:
, (1)
where y is an unknown function of, say, t . If we let
,
then the system (1) can be written in the form
Y' = AY (2)
Any function of the form
y = Cexp(at), C is an arbitrary constant,
satisfies each equation of the system, therefore, it can be represented in matrix form as:
.
It can be easily shown that a vector function Y is a solution to the
system. Thus if 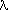 is an eigenvalue of
A and x is an eigenvector belonging to
is an eigenvalue of
A and x is an eigenvector belonging to
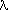 , then
exp(
, then
exp(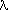 t)x is a solution
to the system (2).
t)x is a solution
to the system (2).
In general, the solution to an n x n first-order system of the form (2) will form an n-dimensional subspace of the vector space of all continuous vector-valued functions. If in addition, we require that Y(t) take on a prescribed value Y0 when t = 0, the problem will have a unique solution; this is shown in any introductory course in elementary differential equations. A problem of the form
Y' = AY , Y(0) = Y0
is called an initial value problem.
To solve the system
,
we start with the matrix
.
The eigenvalues of A are 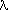 1
= 6 and
1
= 6 and 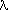 2 = -1. Solving
2 = -1. Solving
(A -I)x = 0
with 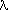 =
=
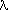 1 and
1 and
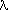 =
=
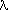 2, we see that x1 =
(4,3)T is an eigenvector belonging to
2, we see that x1 =
(4,3)T is an eigenvector belonging to
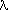 1 and x2 =
(1,-1)T is an eigenvector belonging to
1 and x2 =
(1,-1)T is an eigenvector belonging to
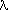 2. Thus any vector function of the
form
2. Thus any vector function of the
form
is a solution to the system.
Suppose also that we require that y1 = 6 and y2 = 1 when t = 0. Thus
,
and it follows that C1 = 1 and C1 = 2. Hence the solution to the initial value problem is given by
.
1. Consider rabbits and foxes that live in the same forest. Their population at time t are x1 and x2. Suppose that the initial populations are x1(0) = 50 and x2(0) = 20. If the growth rates of the species are given by
x'1(t) = -3x1(t) + 6x2(t) x'2(t) = x1(t) - 2x2(t)
what is the population of the rabbits and foxes at time t ?
2. Two tanks are connected as shown below:
Note: Top (water) arrow points out to the right; top (mixture) arrow points out to the left; both bottom (mixture) arrows point out to the right.
Initially, tank A contains 200 liters of water in which 60 grams of salt has beed dissolved, and tank B contains 200 liters of pure water. Liquid is pumped in and out of the two tanks at rates shown in the Figure. Find the amount of salt in each tank at time t = 10.
Hint: Assume that the amount of salt in the tanks are two unknowns functions of time.
 The Course Text, Section 5.1
(Application), Section 8.6
The Course Text, Section 5.1
(Application), Section 8.6
 References from Further
Readings sub-section of Section 8.6.
References from Further
Readings sub-section of Section 8.6.

[ Back to COURSE MINI PROJECTS ]
[ Project 1 | Project 2 | Project 3 | Project 4 | Project 5 ]
[ Course Information | Home Work Assignments | Mini Projects | Maple Exercises | What's New? ]
![[WPI HomePage]](/Buttons/seal.gif)
|
Department of Mathematical Sciences | Back to Vadim Yakovlev's Professional Page |
|---|