
Linear Algebra I
E'00 Course Information

MA2071
 Mon, Wed (& Fri)
Mon, Wed (& Fri)
 Section E01
Section E01


 Mon, Wed (& Fri)
Mon, Wed (& Fri)
 Section E01
Section E01
 |
Monday (except July 3) |
Tuesday | Wednesday (except June 7) |
Thursday | Friday (June 16, July 7, 14) |
|---|---|---|---|---|---|
| Class Hours & Room |
5:30-7:20 pm @ SH203 |
- | 5:30-7:20 pm @ SH203 |
- | 5:30-7:20 pm @ SH203 |
| Office Hours *) | 12:00-12:50 am | - | - | 5:00-6:00 pm | - |
 Kolman, B., Introductory
Linear Algebra with Applications, 6th Edition, Prentice Hall, 1997.
Kolman, B., Introductory
Linear Algebra with Applications, 6th Edition, Prentice Hall, 1997.
 http://www.wpi.edu/~vadim/LA_I/E00_Info.html
http://www.wpi.edu/~vadim/LA_I/E00_Info.html
| Main Topics: | Course Structure: | |
|---|---|---|
|
Two 2-hour lecture meetings a week Homework assignments Weekly Quiz Weekly Mini Project Weekly Maple Exercise Comprehensive Final Exam |
The 100% course grade is based on:
Weekly Quizzes (25%, 5 times, 5% each),
Mini Projects (30%, 5 Projects, 6% each),
Maple Exercises (15%, 5 Exercises, 3% each),
Final Exam (30%).
Point ranges derived to percents for grades are given by:
| Percentage | 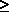 90.00 90.00 |
80.00 - 89.99 | 70.00 - 79.99 |  69.99 69.99 |
|---|---|---|---|---|
| Grade | A | B | C | NR |
Practice problems are given for each topic covered. Unless otherwise is announced, a set of problems associated with the class discussion is assigned in the lecture meetings. You may find the list of the recommended problems in Homework Assignments section of the course web site.
Homework problems are not handed in, so each student should take a personal responsibility for doing sufficient study and practice.
On Wednesdays, there will be 15 min quizzes composed from the homework problems. It will be allowed to use your notes when having the quiz.
Mini Projects:Though this is a distinctive feature in each course topic, the projects are fairly short and not very involved. They look like lengthy exercises, and their main purpose is to emphasize a particular application of the course elements.
The projects are carried out as mostly indepedent studies. Only minimal basics on the relevant subjects are provided in classes and on the web, so to complete the work additional reading and practicing should be undertaken. The course text (Chapter 8) is the major source of required information.
The project descriptions and tasks can be found on Projects page of the course web site.
There are 5 projects, and they should be done at the student's discretion either purely analytically, or with the use of some computer algebra system. (The use of Maple is allowed, but not required.) The printed copies are due in accordance with the Schedule of Events, and each will be worth 30 points.
Maple Exercises:In the course, there are also 5 special assignments to be done with the use of Maple. They will be focused on how few conceptual topics of the course can be illustrated and explored by Maple basic linear algebra commands.
The tasks along with brief descriptions of appropriate Maple commands can be found on Maple Exercises page of the course web site.
The printed reports on these assignments are due in accordance with the Schedule of Events. Each one will be evaluated out of 15 points.
Final Exam:The Final is a comprehensive exam covering the topics of the entire course; it will take 2 hours.
It is an open book & open notes event, and the use of calculators is allowed. However, make sure that all work is shown on paper.
No make up of the Final and late paper submissions will be accepted unless it is caused by a legitimate reason (an illness or other unavoidable emergency) which can be documented.
Bonus Points:There will be opportunities to earn bonus points during this course. Each quiz and the final contains a bonus problem. Also, the outstanding Projects and Maple Exercises can be awarded by bonus points at the instructor's discretion.
Schedule of Events: Independence Day Recess: July 1 -
4
Independence Day Recess: July 1 -
4

[ Course Information | Homework Assignments | Mini Projects | Maple Exercises | What's New? ]
![[WPI HomePage]](/Buttons/seal.gif)
|
Department of Mathematical Sciences | Back to Vadim Yakovlev's Professional Page |
|---|