Linear Algebra I
E'00 Course News & Tips
Info
MA2071 Mon, Wed (& Fri) Section E01



Course Information | Homework Assignments | Mini Projects | Maple Exercises | What's New?




Wednesday, July 5, 2000; 3:10 PM

Answers to the even number problems in the previous Homework Assignments (Sections 4.4 - 4.7):

4.4:
#2a: no
#2b: no

4.5:
#4: {[4, 3, -2, 1, 0], [1, 1, -2, 0, 1]}

4.6:
#4: {(1,0,0,0), (0,1,0,0), (0,0,1,0), (0,0,0,1)}

4.7:
#2: (3,2,-1)
#8: (3,1,3)
#22: (1,1,-1)





Wednesday, June 28, 2000; 2:30 PM

Answers to the even number problems in the previous Homework Assignments (Sections 3.2, 3.3, 3.6, 4.1 - 4.3):

3.2:
#10a: sqrt(14)
#10b: sqrt(30)
#12b: sqrt(6)
#12c: sqrt(13)

3.3:
#4b: yes
#4c: yes
#30: (a) 160 61 123 47 43 17 102 40; (b) OF COURSE

3.6:
#2b: -x + 1 = 0
#2c: y + 4 = 0
#10a: x - z + 2 = 0
#10b: 3x + y - 14z + 47 = 0

4.2:
#10:

Let w1 = a1u + b1v and w2 = a2u + b2v be two vectors in W. Then:

w1 + w2= (a1u + b1v) + (a2u + b2v) = (a1 + a2)u + (b1 + b2)v

is in W. Also, if c is a scalar, then

cw1 = c(a1u + b1v) = (ca1)u + (cb1)v

is in W. Therefore, W is a subspace of R3 (3-space).

#22: (a) and (b)

4.3:
#2d: yes
#10a: no
#10b: (2, 6, 5) = (4, 2, 1) - 2(1, -2, 3)





Wednesday, June 21, 2000; 3:30 pm

In order to feel the concept of Linear Transformations better, consider the following example of an application of LTs.

Cartoonist's Question

Modern cartoonists uses computers and Linear Algebra to transform images they draws. Suppose they are interested in conveying the sensation of motion by gradually tilting and stretching (horizontally) the image of Fig.1 (a) to get that of Fig.1 (b).

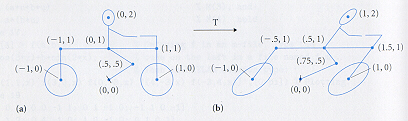Two Cartoons Fig.1

If the necessary gradual stretching along the x-axis is 50%, how can they model this situation and have a computer draw the tilted image? The method should be independent of the initial image (frame) so it can be applied to other frames.

As you see from the course material, the answer to this question involves a simple matrix-vector multiplication. In fact, what one needs to do is multiply the coordinate vector of any plane point that we want to transform on the left (Fig.1, (a)) by some matrix.





Wednesday, June 21, 2000; 3:00 PM

Answers to the even number problems in the previous Homework Assignments (Sections 1.5 - 1.6, 2.1 - 2.2, 3.1):

1.5:
#2a: a11 = 1, a12 = 0, a13 = 3, a21 = 5, a22 = -1, a23 = 5, a31 = 4, a32 = 2, a33 = 2, a41 = -3, a42 = 1, a43 = 4
#2b: a11 = 1, a12 = 0, a13 = 3, a21 = -3, a22 = 1, a23 = 4, a31 = 12, a32 = 6, a33 = 6, a41 = 5, a42 = -1, a43 = 5
#2b: a11 = 1, a12 = 0, a13 = 3, a21 = -3, a22 = 1, a23 = 4, a31 = 4, a32 = 2, a33 = 2, a41 = 2, a42 = -1, a43 = -4
#8c: x = 1, y = 1, z = 0
#10b: x = 1 - r, y = 3 + r, z = 2 - r, w = r
#10c: No solution

1.6:
#4: Singular
#6a: Singular
#6b: a11 = 1, a12 = -1, a13 = 0, a21 = 3/2, a22 = 1/2, a23 = -3/2, a31 = -1, a32 = 0, a33 = 1
#10a: a11 = 3/5, a12 = -3/5, a13 = -2/5, a21 = 2/5, a22 = 3/5, a23 = -4/5, a31 = -1/5, a32 = 2/5, a33 = 2/5
#10b: Singular
#14: a11 = -1, a12 = -4, a21 = 1, a22 = 3

2.1:
#2a: even
#2b: odd
#2c: even
#6a: 2
#6b: 24

2.2:
#6b: -20
#6c: -20
#14b: nonsingular
#14c: singular
#22: x = 22/5, y = - 26/5, z = 12/5

3.1:
#6a: (1,7); (-3,-1); (-2,6); (-7,1)
#6b: (1,-1); (-9,-5); (-8,-6); (-22,-13)
#6c: (1,2); (5,2); (6,4); (13,6)
#8a: x = -2, y = -9
#8b: x = -6, y = 8
#22b: -1/(sqrt(2)sqrt(41))
#22c: -4/(sqrt(5)sqrt(13))
#24b: u1 and u5; u4 and u6
#24c: u1 and u3; u3 and u5





Wednesday, June 14, 2000; 3:30 PM

Answers to the even number problems in the previous Homework Assignments (Sections 1.1 - 1.4):

1.1:
#8: No solution
#12: No solution

1.2:
#6: (a) (A)T = [aTij]; a11 = 1, a12 = 2, a21 = 2, a22 = 1, a31 = 3, a32 = 4;
((A)T)T = [aTij]; a11 = 1, a12 = 2, a13 = 3, a21 = 2, a22 = 1, a23 = 4
(b) A = [aij]; a11 = 5, a12 = 4, a13 = 5, a21 = -5, a22 = 2, a23 = 3, a31 = 8, a32 = 9, a33 = 4
(c) A = [aij]; a11 = -6, a12 = 10, a21 = 11, a22 = 17
(d) A = [aij]; a11 = 0, a12 = -4, a21 = 4, a22 = 0
(e) A = [aij]; a11 = 3, a12 = 4, a21 = 6, a22 = 3, a31 = 9, a32 = 10
(f) A = [aij]; a11 = 17, a12 = 2, a21 = -16, a22 = 6

1.3:
#2: (a) 4; (b) 0; (c) 1; (d) 1
#14: col1(AB) = 1[1 2 3]T + 3[-2 4 0]T + 2[-1 3 -2];
col2(AB) = -1[1 2 3]T + 2[-2 4 0]T + 4[-1 3 -2]
#16:
-2x - y + 4w = 5
-3x - 2y + +7z + 8w = 3
x + 2w = 4
3x + z + 3w = 6
1.4:
#2: A(BC) = {a11 = -2, a12 = 34, a21 = 24, a22 = -9}
#14a: a11 = -3, a12 = -2, a21 = 4, a22 = 1
#14b: a11 = -24, a12 = -30, a21 = 60, a22 = 36




[ Course Information | Homework Assignments | Mini Projects | Maple Exercises | What's New? ]

[WPI HomePage] Department of Mathematical Sciences Back to Vadim Yakovlev's Professional Page

vadim@wpi.edu
Last modified: Wed, July 5, 2000