Modeling

  This text begins with models and uses them throughout. But few of us have the time to pursue every model in full detail through the complete cycle of derivation, analysis, and interpretation. The following are suggestions for three different approaches, listed in increasing order of course time required.

• []own approach is to mix the three approaches, using less and less class time for modeling and depending more and more on the student own work as the term progresses. The expectation that students will assume increasing responsibility for their own learning as the course progresses is reinforced by class discussions in lecture and recitation sections, by the homework exercises assigned, and by the questions posed on sample and actual examinations.

1.

``Take my word for it'': Simply state the governing equations, and perhaps assign reading of the relevant pages from the text, without further class discussion. This approach is not satisfactory as the only introduction to mathematical modeling, but it is appropriate once students have gained some experience with modeling.

2.

Plausibility argument: State the governing equations. Then give a plausibility argument for the terms in the equation, or lead students to develop their own arguments through a class discussion, or assign exercises that require such an argument.

For example, the text only provides a plausibility argument for the competition equations (2.33-2.34)

in subsection 2.4.3, p. 72. Then exercise 5 of section 2.4, p. 75, guides students through a step-by-step derivation.

To provoke class discussion that builds intuitive confidence in a model, consider using Stop and think questions such as 2.21, p. 67, or 2.24 and 2.25, p. 70.

3.

First principles Mimicking the derivation of the model of vertical motion in section 1.2, p. 1-5, or the simple population model in section 2.1, p. 27-31, introduce and motivate the relevant experimental facts and observations (e.g., force of gravity is proportional to mass), introduce the governing physical law (e.g., F = ma), then derive the differential equation(s) and initial condition(s).

• []of the models in the text are derived in this relatively careful manner, but I think it a mistake to plod through every single equation in such detail in class. Instead, some can be derived and discussed carefully in class, some can be stated with a quick plausibility argument, and others can rely on students ``taking your word for it.'' The text is available for back-up reading assignments, and the importance given such reading assignments will be determined by the homework exercises you assign and the test questions you ask.

• []examples of exercises that support the middle road, a plausibility argument for a model, consider:
  • Chapter 2 chapter exercises, exercise 15, p. 79: An insect population (denoted by y) is being destroyed by an insecticide at a constant rate d. It is increasing at a rate proportional to the current population; the constant of proportionality is g. Which of the following initial-value problems might be a reasonable model of this situation? Justify your rejection of each unacceptable choice.

    (a)

    $y' + gy = d, \; y(0) = y_{i}$

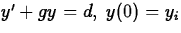
    (b)

    $y' - gy = d, \; y(0) = y_{i}$

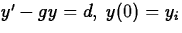
    (c)

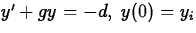
    $y' + gy = -d,\; y(0) = y_{i}$

    (d)

    $y' - gy = -d, \; y(0) = y_{i}$

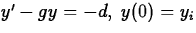
  • Section 5.1, exercise 7, p.217: The text derived the model

    $$mx'' + kx = k(h(t) - h(0)), \; x(0) = x_i, \; x'(0) = v_i,$$

    for the forced, undamped vertical spring-mass system. It also considered a spring-mass system without forcing that was damped by friction. It obtained the model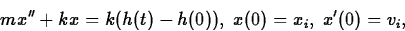

    $$mx'' + px' + kx = 0, \; x(0) = x_i, \; x'(0) = v_i\,.$$

    In fact, even a freely suspended mass is subject to damping due to air resistance and internal resistance in the spring. These damping forces can be modeled as being proportional to velocity and acting in the opposite direction, just like the force of friction acting on the mass sliding horizontally.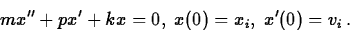

    (a)

    Compare the undamped, forced model with the damped model without forcing. Predict what a model of a forced, damped system would look like.

    (b)

    Verify your prediction by deriving such a model. Specifically, consider the system shown in figure 5.5 and suppose that the mass is subject to air resistance which is proportional to its velocity and acts in the opposite direction.