Diffusion models, ordinary and partial

The stationary diffusion equation with convection but no source, -D( A(x) c'(x) )' +( A(x) V(x) c(x) )' = 0, is derived in section 9.1, Diffusion Models, p. 428-433. Derivations of various thermal analogs are requested in section 9.1, exercises 9-14. Diffusion models provide the examples used in sections 9.2, Boundary-value Problems: Analytic Tools, and 9.3, Boundary-value Problems: Numerical Methods. The equation for diffusion in a circular domain (e.g., example 2, p. 432) is used in section 11.2, Cauchy-Euler Equations, as an example of such an equation.

The heat equation 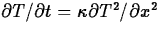$\partial T/\partial t = \kappa \partial T^2/\partial x^2$ is derived in section 9.4, Time-Dependent Diffusion, to provide the motivating example for the two subsequent sections, 9.5, Fourier Methods, and section 9.6, Initial-Boundary-Value Problems: Numerical Methods. Separating the heat equation on a circular domain also provides an example of a Bessel equation for section 11.5, Regular Singular Points.