Oscillatory models

The classic spring-mass harmonic oscillator equation mx'' + px' + kx = F(t) and its equivalent first-order system are derived in section 5.1, p. 203-215, the linear and nonlinear pendulum equations (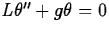$L \theta'' + g \theta = 0$, etc.) and their equivalent first-order systems in section 5.2, p. 219-221. The linear spring-mass model is used extensively in chapter 6 Analytic Tools for Two Dimensions, which develops the usual second-order analytic solution methods and applies them to analyze the behavior of these systems.

The nonlinear pendulum equation 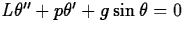$L \theta'' + p \theta' + g \sin \theta = 0$ is the nonlinear foil to the simple harmonic oscillator for the study of equilibria, linearization, nullclines, stability, etc. It and its linear relative are used repeatedly in section 6.8, Linear versus Nonlinear, p. 321-325, in section 7.1, The Phase Plane, p. 334-339, in section 7.2, Nullclines and Local Linearization, p. 343-350, and in section 8.3, Connections with the Phase Plane, the study of linearized phase plane analysis.