



Next: My preferences
Up: Modeling
Previous: Maximal modeling
One corner of the modeling triangle is deriving mathematical
statements from experimental observations and physical laws.
Another is using mathematical concepts--analytical, graphical,
and numerical--to analyze the behavior predicted by the model.
The third is interpreting that behavior in light of the original
physical problem. Tables 3,
4, and 5
summarize the mathematical concepts that are associated with the
analysis and interpretation of many of the models introduced in
this text.
From a modeling point of view, the best approach to constructing
a syllabus is to decide which ideas you regard as most important
and which models are likely to be of most interest to you and
your students. Use tables 3,
4, and 5 to
strike the balance that is best for you--the left-hand columns
of those tables list models, the right-hand columns list the
ideas that are introduced using those differential equations.
The time you spend in your course with analysis and
interpretation is time in part devoted to modeling and time in
part devoted to mathematics. For many students, seeing
mathematics explain physical phenomena is the most powerful
motivation for its study. From that perspective, you might
decide to choose the models you emphasize by the ideas that are
exemplified in their analysis, that is, by selecting solely from
the right-hand column of tables 3,
4, and 5.
Table 3:
Analytical,
numerical and graphical tools used in analyzing first-order
models. The center column identifies the section in which the
ideas listed in the right-hand column are used to analyze the
given model. See tables 1 and
2 for the section in which each model
is introduced.
| 3cIdeas Used in Analyzing First-Order Models |
|
|
|---|
| 1l|Model |
Section |
Ideas used |
|---|
| 1l|Projectile motion |
|
|
|---|
| Rock model: v' = -g |
1.2 |
direction field, solution graph |
| |
|
Euler's method, solution formula |
| |
3.2 |
direction field, solution graph |
| 1l|Scalar population |
|
|
|---|
| Simple: P' = kP |
2.1 |
direction field, solution graph, |
| |
|
solution formula |
| |
3.1 |
Euler's, Heun's methods |
| |
3.2 |
direction field, solution graph, |
| |
4.1 |
general solution |
| |
4.2-4.3 |
solution formula |
| Emigration: P' = kP - E |
2.2.1 |
direction field, solution graph, |
| |
|
steady state, stability |
| |
3.2 |
direction field, solution graph, |
| |
|
phase line |
| |
3.3 |
steady state, stability |
| |
4.1 |
general solution |
| |
4.2, 4.4 |
solution formula |
| |
10.4-10.5 |
Laplace transform
solution |
| Logistic: P' = aP - s P2 |
2.2.2; 3.2 |
direction field, solution graph, |
| |
|
phase line |
| |
3.3 |
linear stability analysis |
| |
4.2 |
solution formula |
| |
4.6 |
uniqueness |
| 1l|Heat flow |
|
|
|---|
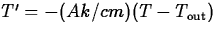 |
2.3 |
direction field, solution graph, |
| |
|
steady state, stability, |
| |
|
Euler's method |
| |
3.1 |
Euler's, Heun's methods |
| |
3.2 |
phase line |
| |
3.3 |
steady state, stability |
| |
4.1 |
general solution |
Table 4:
Analytical,
numerical and graphical tools used in analyzing higher-order
models. The center column identifies the section in which the
ideas listed in the right-hand column are used to analyze the
given model. See tables 1 and
2 for the section in which each model
is introduced. (Continued in table
5.)
| 3cIdeas Used in Analyzing Higher-Order Models |
|
|
|---|
| 1l|Model |
Section |
Ideas used |
|---|
| 1l|Multi-species population |
|
|
|---|
| Predator-prey (2.24-2.25), p. 67 |
2.4.1 |
steady state,
stability, |
| |
|
Euler's method |
| Epidemic (SIR, SIRS) |
2.4.2 |
steady state, stability, |
| (2.29-2.30), p. 71 |
|
phase plane |
| |
7.2 |
nullclines, local
linearization |
| Competition (2.35-2.36), p. 73 |
2.4.3 |
steady state, phase
plane |
| 1l|Oscillators |
|
|
|---|
| Spring-mass: |
|
|
| mx'' + px' + kx = F(t) |
5.1 |
solution formula, phase plane, |
| |
|
Euler's method |
| |
6.1 |
general solution |
| |
6.3-6.5 |
solution formulas
(homogeneous: |
| |
|
undamped, overdamped, etc. |
| |
6.6-6.7 |
solution formulas
(nonhomogeneous: |
| |
|
resonance, etc.) |
Pendulum: 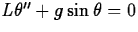 |
5.2 |
linearization, solution
formula |
| |
6.1 |
steady state, linearization |
| |
6.5, 6.8 |
solution formula (linear) |
| |
6.8 |
steady state, linear stability |
| |
7.1 |
phase plane |
| |
7.2 |
nullclines, local
linearization |
| |
8.3 |
linear stability analysis, |
| |
|
phase plane |
| van der Pol: |
|
|
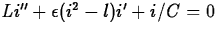 |
7.3 |
limit cycle |
| 3cIdeas Used in Analyzing Higher-Order Models (cont'd) |
|
|
|---|
| 1l|Model |
Section |
Ideas used |
|---|
| 1l|Steady diffusion |
|
|
|---|
| -D(A c')' +(A V c)' = 0 |
9.2 |
solution formula |
| |
9.3 |
numerical approximation |
| |
|
(finite differences) |
| |
11.2 |
solution formula |
| 1l|Time-dependent diffusion |
|
|
|---|
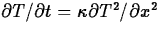 |
9.5 |
eigenfunction solution |
| |
9.6 |
numerical approximation |
| |
|
(method of lines), |
| |
|
equilibria |
| |
11.5 |
spatial eigenfunctions |
| |
|
(Bessel) |
caption
[Ideas Used in Analyzing Higher-Order Models (cont'd)]
Continuation from table 4
of the list of analytical, numerical and graphical tools used in
analyzing higher-order models. The center column identifies the section in which the
ideas listed in the right-hand column are used to analyze the
given model. See tables 1 and
2 for the section in which each model
is introduced.




Next: My preferences
Up: Modeling
Previous: Maximal modeling
Paul W Davis
5/5/1999