Graphical Abstract
This course, taught by Kevin Crowthers, Ph.D., introduces us to technical scientific writing, such as grant proposals, theses, and more. One major project for this class is our Independent Research Project. Shown below is a brief introduction to my persional Independent Research Project.
Exploring Order-3 Maximal Independent Sets in Lattice-Torus Product Graphs
This project explores Order-3 Maximal Independent Sets, a refined version of Maximal Independent Sets that remains independent under small nodal perturbations. While standard MIS are widely used in network theory for tasks like communication systems, fraud detection, and marketing, they often lack a metric for measuring packing stability and uniformity. By counting Order-3 MIS and analyzing their patterns in torus, lattice, and cylinder graphs, we uncover structural insights that could improve network design and combinatorial optimization. This project's findings reveal both pure exponential growth in certain cases and inductive patterns in others, highlighting new combinatorial behaviors that contribute to graph theory and its applications.

What relationships exist in the number of order-3 maximal independent sets on graphs formed by the cartesian product of torus and lattice graphs?
How can formulas be developed for the number of order-3 maximal independent sets on lattice-torus product graphs and relationships pseudoprimes generated by cyclic symmetries?
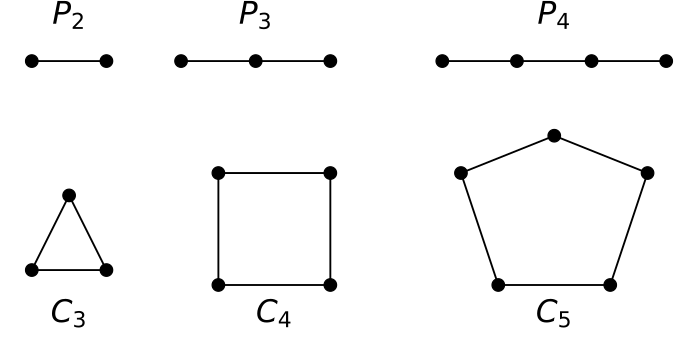
A maximal independent set (MIS) is a set of vertices that cannot be enlarged without violating the independence condition. This concept plays a crucial role in various fields, including network design, scheduling, and resource allocation, where maximizing the number of elements is desirable in an independent set. Despite the extensive study of maximal independent sets, their properties under specific conditions, such as disturbances or disruptions to the set, remain underexplored.
To address the need of creating metrics by which packing optimality can be determined in a MIS, researchers have extended the concept of MIS to Order-k Maximal Independent Sets (Yanco & Bagchi, 1994). An Order-k MIS is a set that cannot be enlarged by adding or removing k vertices while maintaining the independence property. This generalization allows MIS to be categorized by how tightly their vertices are packed and how resistant it is to small perturbations.
Research on Order-k MIS has focused on primitive graph types, such as cycle and path graphs (Yanco & Bagchi, 1994). Studies have found that the number of Order-k MIS on cycle graphs follows specific patterns, often related to the properties of the graph’s order. However, these studies have largely been limited to cycles and paths, and the behavior of Order-k MIS on more complex graph structures remains unexplored.

Lattice-Torus Product Graphs were constructed as Cartesian products of path graphs and cycle graphs. Graphs were generated programmatically as lists of lists, where each sub-list was a set of pointers to all adjacent vertices, since this was all data required, and allowed for general graphs to later be inputted into the other algorithms if tests of non-lattice-torus product graphs were required.
A backtracking algorithm was implemented to identify all MIS efficiently and verify their Order-3 maximality. For each candidate MIS, perturbations involving up to three vertex additions/removals were tested. If no larger independent set could be formed through these perturbations, the set was classified as Order-3 MIS.
Experiments were conducted on graphs with dimensions n,m for n+m≤14 for computational feasibility. For each graph type (cylinder, lattice, torus), the graph data type was created, and the algorithm was used to count Order-3 MIS. Data was printed to log for subsequent pattern analysis.
Linear recurrence relations were hypothesized for sequences of Order-3 MIS counts. Inverse matrix methods were applied to identify coefficients of potential recurrence relations.
The numbers of Order 1 MIS on Lattice Graphs
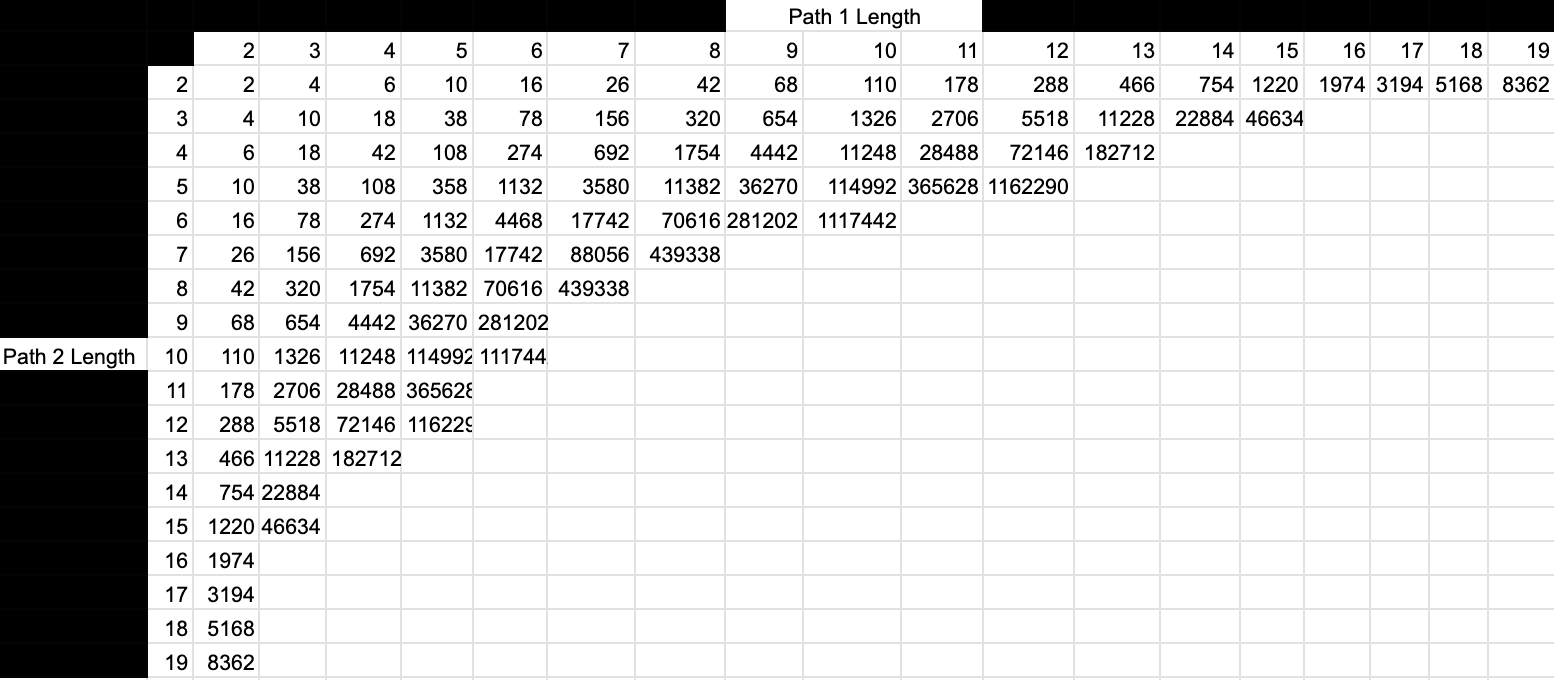
The numbers of Order 3 MIS on Lattice Graphs
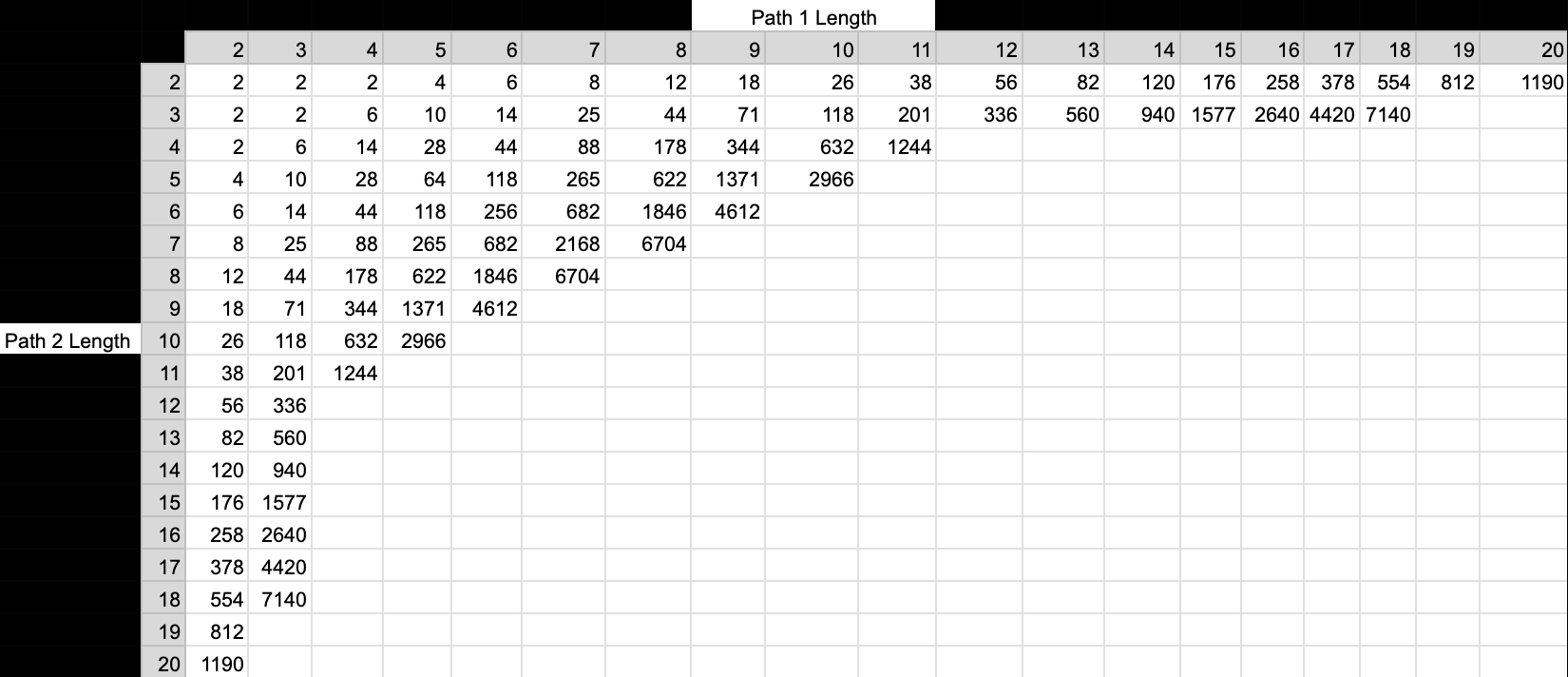
The numbers of Order 1 MIS on Cylinder Graphs
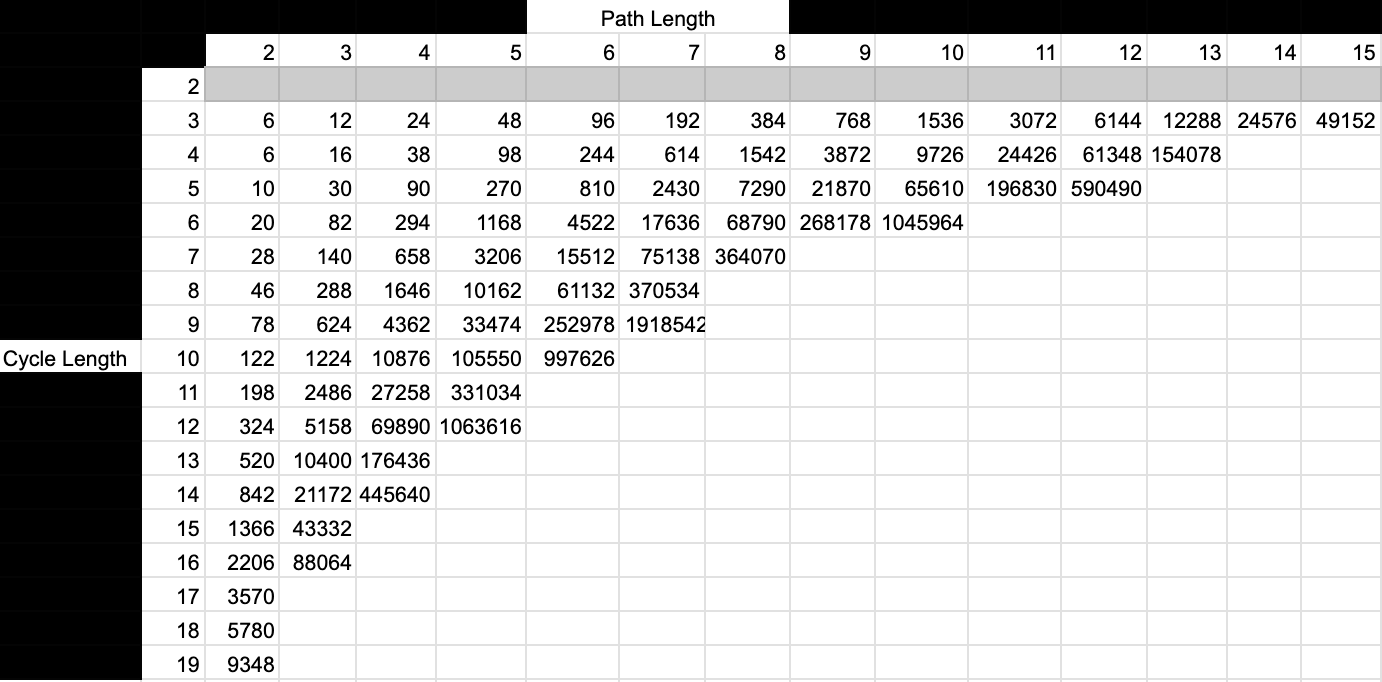
The numbers of Order 3 MIS on Cylinder Graphs
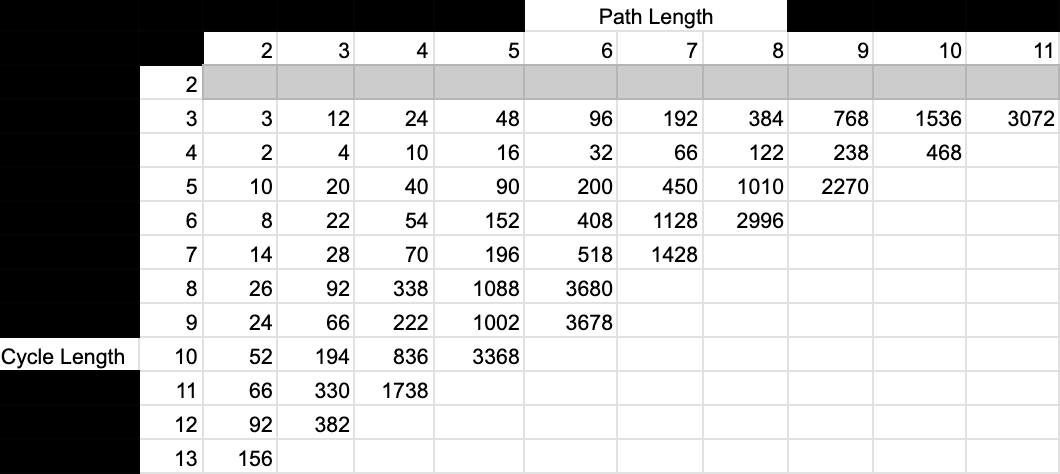
The numbers of Order 1 MIS on Torus Graphs
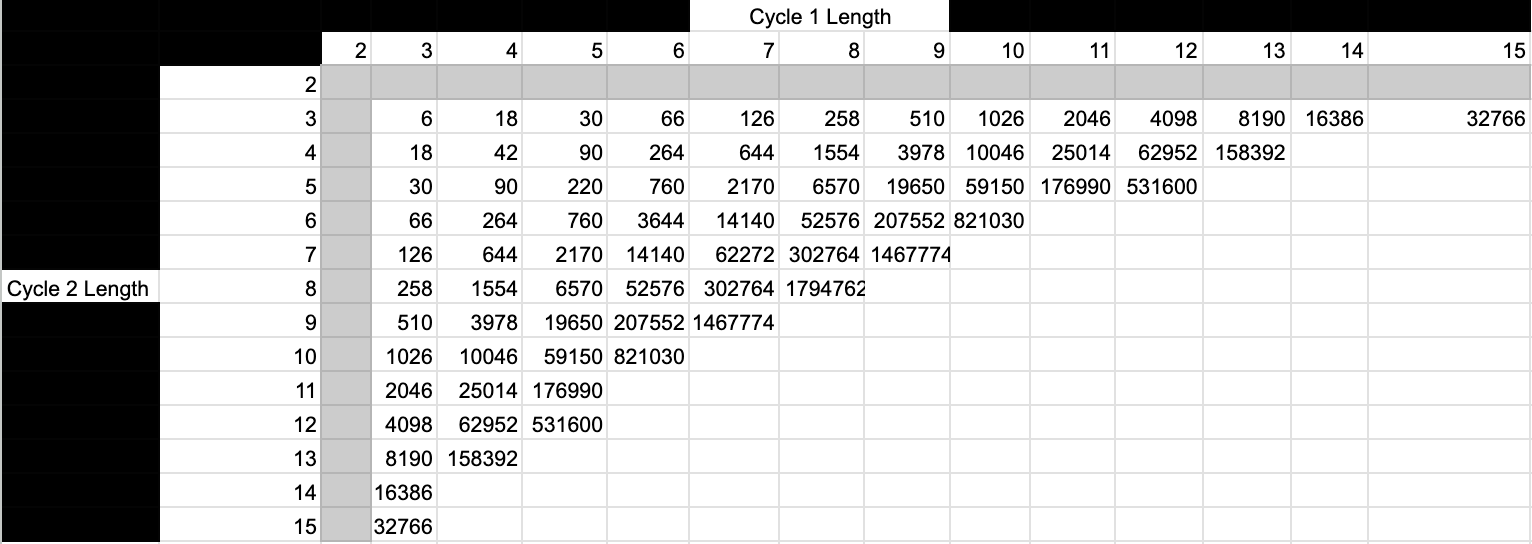
The numbers of Order 3 MIS on Torus Graphs
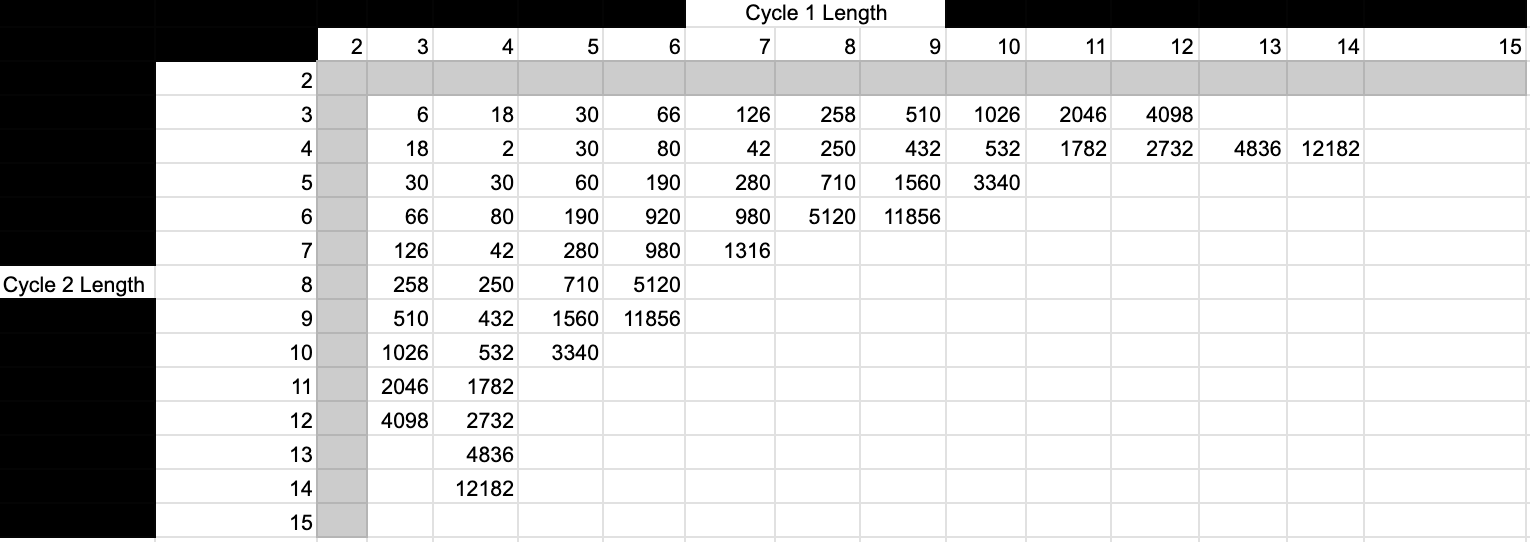
Linear recurrence relations were hypothesized for sequences of Order-3 MIS counts. Inverse matrix methods were applied to identify coefficients of potential recurrence relations.
For graphs composed of a path of length 2 or a cycle of length 3, linear recurrence relations were found. Furthermore, for graphs composed of a cycle graph with prime order, the total number of order-3 MIS was found to be a multiple of the cycle order. This is caused by the cyclic symmetries inside the composed graph.
The primary objective was to explore the structural properties of Order-3 MIS in complex graphs and determine if the patterns seen in primitive graphs extend to Lattice-Torus Product Graphs. The analysis of data using inverse matrix methods has led to one key finding thus far:
Using inverse matrices, we identified distinct recursive sequences in the counts of Order-3 MIS for several graph configurations, including:
• Graphs with a cycle and a path of length 2.
• Graphs with a path and a path of length 2.
• Graphs with a cycle and a cycle of length 3.
• Graphs with a path and a cycle of length 3.
These recursive relationships suggest that the structure of the graph components strongly influences the count of Order-3 MIS. The existence of these patterns supports our hypothesis that the inherent structure of Lattice-Torus Product Graphs determines the behavior of MIS, similar to - but more complex than - those observed in simpler graphs (e.g. (Yanco & Bagchi, 1994)).
A further observation is that for cyclic components with prime orders, the total number of Order-3 MIS is consistently a multiple of the order of the cyclic component. This multiplicative behavior indicates a symmetry or regularity in prime-order cycles, suggesting that symmetries in prime cyclic orders could help in understanding the broader behavior of MIS in composite graphs.
Yanco, R., & Bagchi, A. (1994). K-th order maximal independent sets in path and cycle graphs. Retrieved from https://oeis.org/A007380/a007380_1.pdf