Circuits
Introduction to Circuit Elements and Ohm's Law
Objectives
After this chapter you should be able to:
- Identify Circuit Components
- Solve Basic Circuits Using Ohm's Law
- Create Equivalent Resistances From Parallel and Series Resistors
- Solve Basic Circuits Using KVL and KCL
Circuits and Circuit Elements
A circuit is the interconnection of electrical devices in a circular path. To power the circuit, voltage is generated from a power source and moves through the wires and components. Voltage is the total work per unit charge associated with the motion of charge between two points. The rate at which the electrical charge is flowing through a wire or conductor is called current. Both current and voltage are required to achieve electrical power.
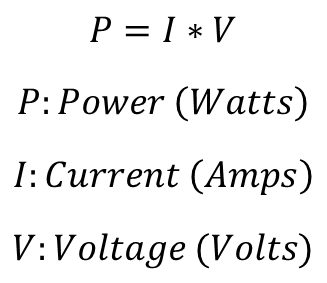
Some people have trouble conceptualizing electricity because they cannot see it. Try considering the circuit to instead be a system of pipes. Each pipe is essentially a very large wire. The power source, which is essentially a pump, takes in charge with low voltage and outputs charge with high voltage. Similarly, a pump which takes in water of low pressure and pushes out higher pressure water. The flow rate of the water moving through the pipe would be the voltage. Water flows from areas of high pressure to low pressure; likewise, electricity flows from areas of high voltage to low voltage. The speed at which water moves through a pipe is the current. The size of the pipe acts as resistance. If the pipe is very large, the resistance is very low and the water can flow freely; if the pipe is small, the water flow is much more restricted. Small resistors are basically large pipes, and large resistors are small pipes.

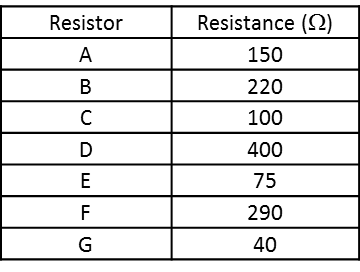
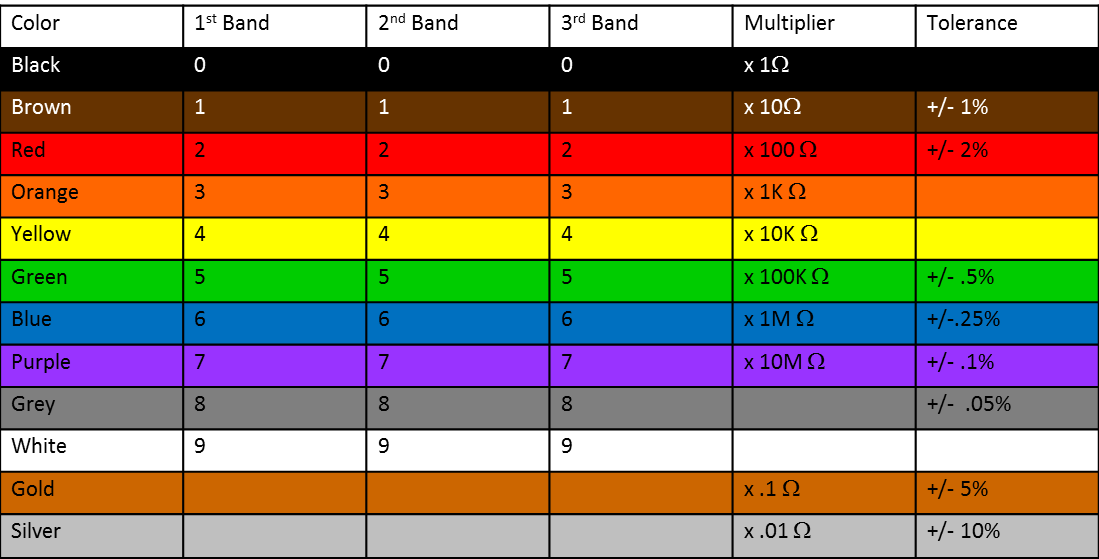
Resistance, measured in Ohms, of an electrical component is when current opposes, or resists, flowing through that component. The most common electrical component to induce resistance is a Resistor. It is important to remember that resistors always dissipate power. Resistors are color coded to show how much they will oppose current. Most resistors have two or three colored bands to denote the resistance followed by either a silver or gold band to denote the tolerance level

Ohm's Law
Resistance and current can be used to determine voltage with Ohm's Law. Ohm’s law is the most important equation for basic circuitry.
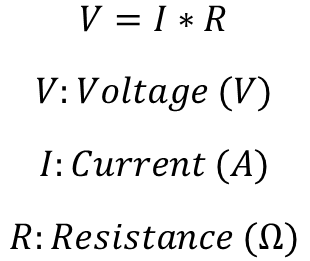
That equation can then be substituted into the Power equation from before.
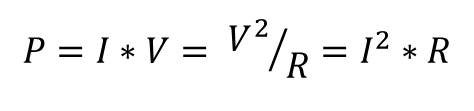
Add or remove batteries and change the resistance to see how the variables in the formula change. Click the "Instructions" button for additional information.
More Vocab:
Node: A point in a circuit where two or more components are connected
Loop: An ordered sequence of nodes forming a closed path
Parallel and Series Resistors
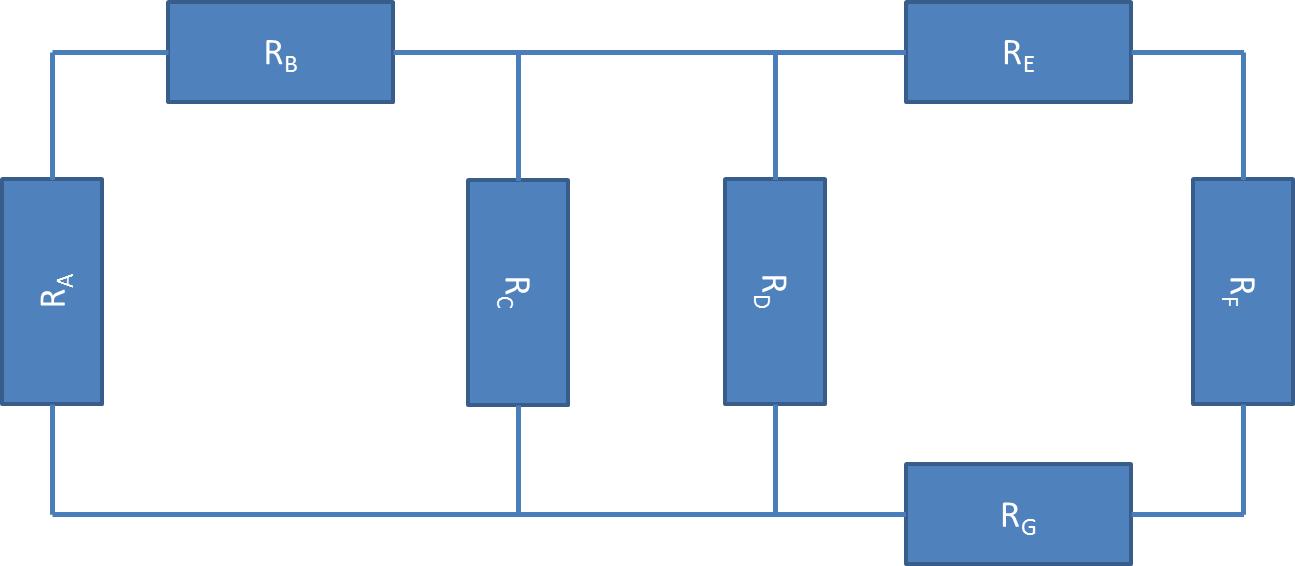
Solving a circuit requires simplifying by combining similar elements. In order to for a circuit with multiple resistors to be solved, the resistors must first be simplified into one total, equivalent resistance. The first step to simplifying resistance is determining whether the resistors are in series or parallel.
Two elements are in series if they share a node with no other elements connected at the node. Resistors in series add together to get an equivalent resistance. In the figure below, resistors A and B are in series. Two elements are in parallel if they form a loop with no other elements in the loop. Resistors in parallel combine by adding the reciprocal sum of each value. In the figure below, resistors C and D are in parallel.
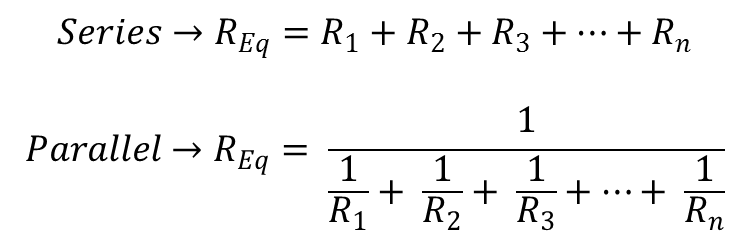
Here's an example:
Try to reduce the circuit above. Click on the circuit for the solution.
Explanation of Series and Parallel
Why do series resistors simply add together while parallel ones are so much more different? The reasoning lies in how the current moves through the circuit. When resistors are in series current is able to flow through all of the resistors in a single loop. So the equivalent resistance of series resistors has to be larger than the largest resistor in the circuit. However when resistors are in parallel the current has to split between the loops created by the parallel resistors. This means that the equivalent resistance will always be smaller than the smallest resistor in the loop. It is important to note that when current flows through a loop of parallel resistors, it splits in a way that is proportional to the resistance of the resistors; higher resistors will have less current flowing through them and vice versa to ensure that there is the same amount of voltage going through the entire circuit.
Kirchoff's Voltage and Current Laws
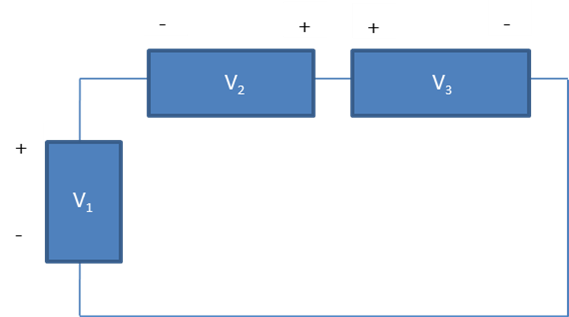
Kirchoff's Voltage Law(KVL) says that the algebraic sum of the voltages around a loop is zero. To solve a circuit with KVL sum all the voltages, paying attention to the polarity of the voltage sources.
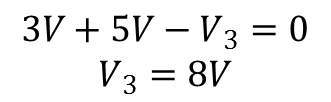
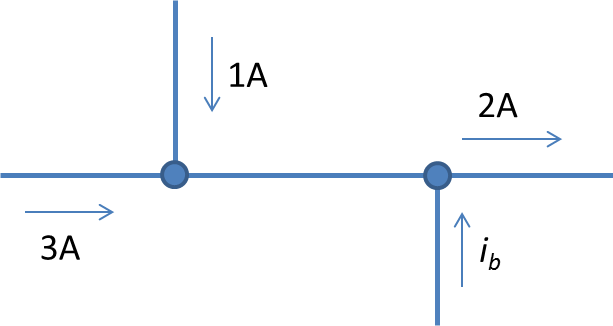
Kirchoff's Current Law(KCL) says that the algebraic sum of all the currents entering a node is zero. To solve a circuit with KCL, the sum of all the currents leaving a node should be subtracted from all currents entering that same node with any unknown values left as variables.
In the drawing to the right, the two nodes can essentially be considered one node. This is because there are no electrical components between them. Remember that changing the sign of the current will change the direction in which it is travelling.
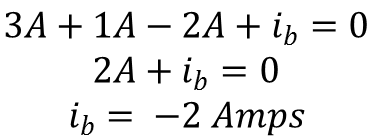
Concept Questions
Section Vocab
Circuit: The interconnection of electrical devices in a circular path
Voltage: Total work per unit charge associated with the motion of charge between two points. Measured in Volts(V)
Current: The rate at which the electrical charge is flowing through a wire or conductor. Measured in Amps (A)
Resistance: Opposes, or resists, current flowing through that component
Resistor: Electrical element to induce resistance
Ohm's Law: Voltage = Current*Resistance (V=IR)
Node: A point in a circuit where two or more components are connected
Loop: An ordered sequence of nodes forming a closed path
Series: Elements that share a node with no other elements connected at the node
Parallel: Elements that form a loop with no other elements in the loop
Kirchoff's Voltage Law: The algebraic sum of the voltages around a loop is zero
Kirchoff's Current Law: The algebraic sum of all the currents entering a node is zero