William C. Sanguinet
Assistant Teaching Professor
The three dimensional butterfly is an animation that I made using Maple. To make the animation I just used some calculus and linear algebra.
My 3D butterfly is based off of the 2D parametric plane curve discovered by Temple H. Fay in 1989.
First, I figured out how to correctly parametrize the z coordinate to allow for the butterfly to be brought into 3D. After this, I was able to produce a oscillatory flapping motion. Lastly, I applied a rotation matrix to the butterfly to ensure that it turns while it moves around the origin.
First, I figured out how to correctly parametrize the z coordinate to allow for the butterfly to be brought into 3D. After this, I was able to produce a oscillatory flapping motion. Lastly, I applied a rotation matrix to the butterfly to ensure that it turns while it moves around the origin.
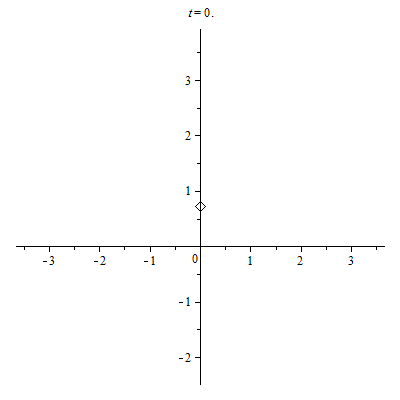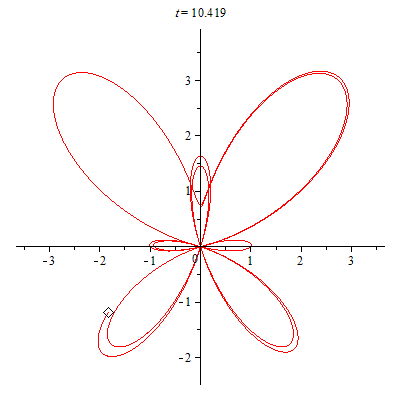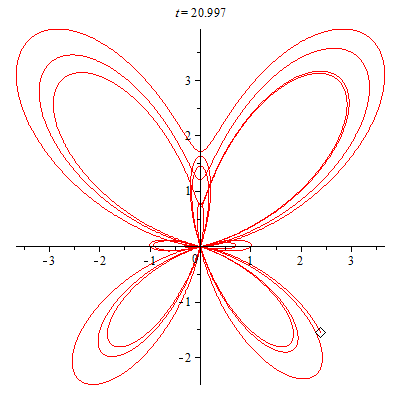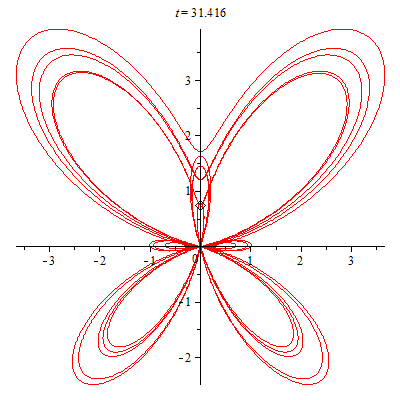

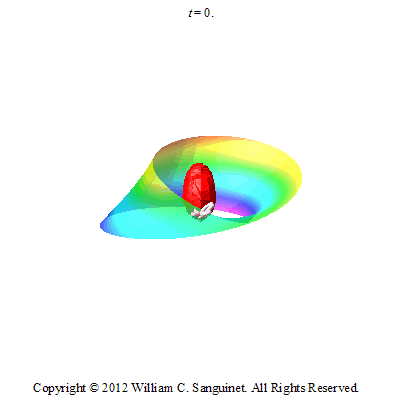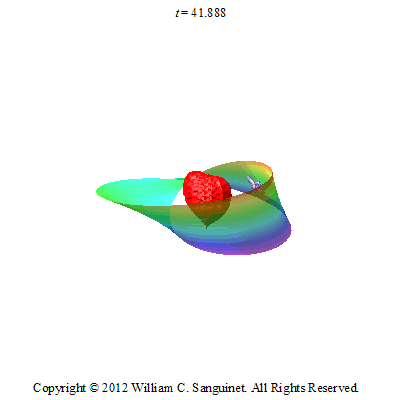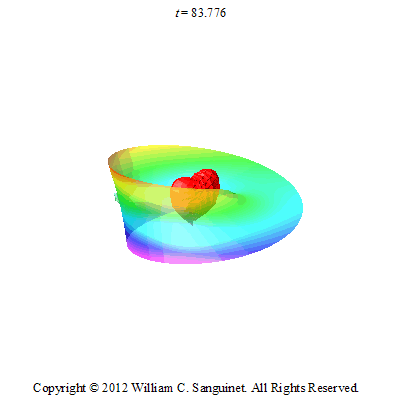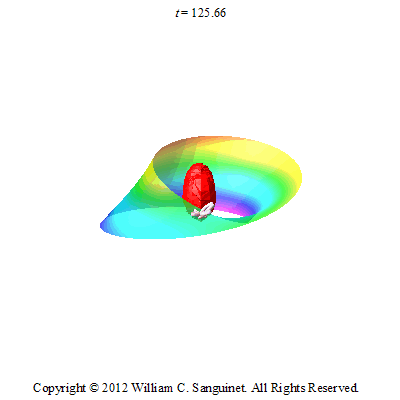
In 2011/2012, I wanted to do something a bit more difficult with the butterfly. I decided to make it fly around a Mobius strip.
When I was making a different maple demonstration, I came up with the idea of creating a beating heart.
Below you see the two individual animations, as well as the final product.
To make the animation I used some very basic differential geometry and calculus. For the first animation (butterfly on Mobius strip), I parametrically defined the Mobius strip, and then plotted it in an orthonormal frame on the surface of the strip.
To make the animation I used some very basic differential geometry and calculus. For the first animation (butterfly on Mobius strip), I parametrically defined the Mobius strip, and then plotted it in an orthonormal frame on the surface of the strip.