Home Pages of Ted Clancy
RESEARCH INTERESTS
Wearable Wireless
Medical & Health Sensors
We have several emerging projects in which we
are designing wireless medical/health sensors that are wearable.
In one project, we are designing a small prototype wireless electromyogram
(EMG) sensor. While such a sensor can be used generally, we are tailoring
this sensor specifically for use as the control input to myoelectric
prostheses—initially hand and hand-wrist prostheses. We have
other emerging project interests in other biosignals related to
physiological monitoring and various assistive devices.
These wearable sensors are an excellent fit
to the field of Electrical and Computer Engineering (ECE). Typically,
the front end of the wireless node requires analog design to
interface and transduce the physiological signal, the signal
is then acquired and processed on a low-power microcomputer
(requiring fundamental knowledge in computer engineering
and signal processing), the signal is transmitted wirelessly
to a base station (or "The Cloud"), and then more advanced
signal processing/machine learning is applied to interpret
the data. The skills required for development of these
sensors span most of the field of ECE. Dependending on the
specific project, of course, there are opportunities for work
that spans these various sub-disciplinary areas or for work
that "dives deep" into any one area.
Electromyogram (EMG) Amplitude
Estimation
The electromyogram, or EMG, is the electrical activity
produced by skeletal muscles during contraction. When individual
motor units (motor units are the smallest functional grouping of muscle
fibers) contract, they repetitively emit a short burst of electrical activity
known as a motor unit action potential. The time between successive
bursts is somewhat random for each motor unit. When several motor
units are active (the timing of the electrical burst between distinct motor
units is mostly uncorrelated), a random interference pattern of electrical
activity results. Observed at the skin surface by conventional bipolar
electrodes, the interference pattern can be modeled as a zero-mean stochastic
process. To modulate muscle tension, the number of active motor units
is modulated and/or the average firing rate of active motor units is
modulated. In either case, the standard deviation of the
interference pattern is altered
(it is increased by an increasing number of active motor units and/or an
increase in the firing rate of individual motor units). Thus, the
standard deviation of the interference pattern, generally referred to as
the EMG amplitude (EMGamp), is a measure of muscular activation level.
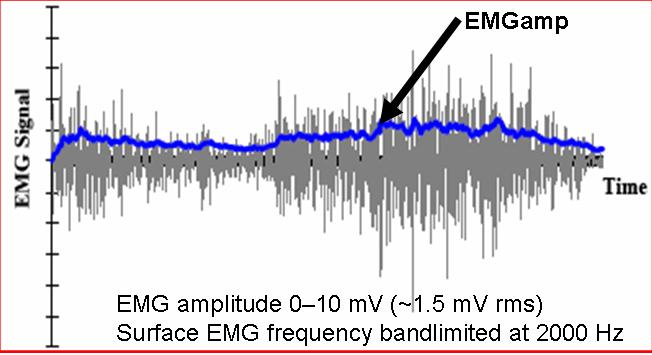Because EMG amplitude is, by definition, a parameter
of a random process, its value can only be estimated from a sample
of an EMG. The work that collaborators and I have been involved in
is in the development of improved techniques for estimating EMG amplitude.
This work has involved the iterative process of (1) using existing theory
and experimental results to develop an improved stochastic mathematic model
of EMG, (2) based on the improved model, determine mathematically optimal
methods for estimating EMG amplitude (as well as determining an objective
quality measure for the new methods), (3) implementing and experimentally
testing the new estimation technique, and (4) adding these results to the
existing theory.
In general, EMG amplitude estimation from an EMG
sample requires six processing steps: (1) noise rejection/filtering, (2)
whitening, (3) multiple-channel combination, (4) detection, (5) smoothing,
and (6) relinearization. A more complete description of these steps,
as well as a review of the present state-of-the-art can be found within
the EMG Amplitude Estimation toolbox.
Development of EMG amplitude estimation techniques is a continuing research
interest.
Relating Surface
EMG Amplitude to Joint Torque
EMG is essentially a by-product of muscle contraction.
The development of muscular tension is the main purpose of contraction.
Hence, it is logical to try to relate the electrical activity of muscle
to its mechanical activity. In general, as the number of active motor
units is increased and/or the average firing rate of active motor units
is increased, both EMG amplitude and total muscle tension increases. However,
the relationship is dynamic and, depending on the resolution desired, may
also need to be treated as non-linear.
It would be ideal, therefore, to relate surface
EMG amplitude to the tension (or, force) produced by individual
muscles. However, there are at least two fundamental difficulties
in doing so. First, classical EMG recorded at the surface of the
skin can contain "cross-talk". That is, EMG from muscles other than
that which the experimenter intends to record may be included in the signal.
Cross-talk is a difficult problem with no immediate, simple solution.
Second, relating EMG to individual muscle tension requires independent
verification via direct mechanical measurement of individual muscle tension.
At present, there is no practical (and perhaps not any) method for
reliably making such measurements.
Because of these fundamental limitations, colleagues
and I have focused our efforts on relating surface EMG amplitude to joint
torque. First, cross-talk, if it exists, may not be as problematic.
Certain cross-talk contributions are automatically removed from the estimated
torque, even if they can not be removed from the individual muscle tension
contributions. Second, net torque about a joint can, in many cases,
be reasonably (or even easily) verified via direct mechanical measurement.
To date, we have examined the EMG-torque relationship
in two simple cases for constant-posture, nonfatiguing contractions about
the elbow. In the first case, slowly force-varying contractions (essentially
no dynamics) were examined and the EMG-torque relationship modeled as a
polynomial relationship. A degree three polynomial (non-linear model)
was found to best describe the relationship. Also, advanced EMG amplitude
estimation algorithms were compared to classical algorithms. The
advanced algorithms gave lower EMG-torque errors. In our second study
case, force-varying contractions were recorded. Linear, dynamic
("black box") system identification techniques were used to relate
EMG amplitude to torque. Again, results indicated that advanced EMG
amplitude estimation leads to lower EMG-torque errors. Relating EMG
amplitude to joint torque is a continuing research interest.
Relating Surface
EMG Amplitude to Joint Impedance
Joint impedance refers to the relationship between
perturbations in joint angle to perturbations in joint torque. That is, if
joint posture is disturbed by applying an external torque about the joint, what
will be the resulting change in joint angle (ignoring adjustments due to
feedback)? Typically, one can decrease the influence of perturbations by
voluntarily increasing impedance via co-activation of antagonists muscles acting
about the joint. Increased impedance is beneficial in many circumstances,
as it serves to reject inevitable external disturbances. However, there
is a metabolic cost to maintaining co-activation, and co-activation increases
the overall workload on the muscles. In many work-related tasks,
constant/frequency muscle activation may be related to cummulative stress
disorders. Thus, we are interested in understanding what mechanical
impedance is generated by various individuals as they perform tasks.
Typically, impedance is measured by applying a
transient force, and then measuring the resulting angle perturbation. In
general, joint impedance is highly non-linear, depending on the type of force
transient applied and the muscle conditions (e.g., joint angle, level of
background muscle activation, fatigue state of the muscle). However, for
small random perturbations applied at one (non-fatigued) muscle condition, the
impedance relationship is well represented as a second-order linear system.
Thus, impedance can be characterized by its stiffness, viscosity and inertia
(which are a function of the "operating point," or muscle condition). For
accurate measurement of impedance, the joint must be perturbed.
In many cases (e.g., ergonomic analysis), an
approximation of the joint impedance would be acceptable, but only if the
impedance could be estimated without perturbing the joint. In this
manner, a worker's impedance could be measure
while performing a task —
and not interrupted by the perturbations. Here, again, surface EMG
amplitude may be useful. Since modulation of impedance is achieved by
modulating muscular effort, we should be able to develop an EMG-impedance
relationship in much the same way that prior researchers have developed an EMG-torque
relationship. At a given operating point, we can measure the agonist and
antagonist EMG amplitude, and the corresponding joint impedance. We can
then relate the EMG amplitudes to joint impedance. We are currently
involving in preliminary work to investigate this relation for conditions which
satisfy the linear second-order model assumptions.
High Resolution EMG Arrays
As noted above, a typical surface EMG signal records
the interference pattern derived from many contributing motor units.
If arrays of small-diameter (≤ 2mm), tightly-spaced (≤ 8mm) EMG
electrodes are used to measure the EMG signal, then weighted combinations
of the recorded signals produce a spatially filtered EMG channel that
can have sufficient resolution to identify individual motor unit
action potentials. There is active research into identifying
optimal spatial filters, electrode array configurations and methods
for using the arrays signals to decompose the EMG signal.
Other EMG-Related Interests
Depending on the opportunity, I'm interested in many other areas of EMG-related
research, including:
- EMG signal changes during sustained (e.g., fatiguing) contractions.
- Use of EMG in clinical applications (neuromuscular assessment,
clinical biomechanics, etc).
Other Biosignal Interests
Other areas of past (and perhaps future) research include:
- ECG and blood pressure analysis: I've studied a phenomenon known
as electrical-mechanical alternans. In electrical alternans, the
shape of the ECG corresponding to alternate heart beats differs.
That is, if the beats are numbered sequentially, all of the odd numbered
beats have one shape and all of the even numbered beats have a second shape.
An analogous sequence occurs in pulsus alternans (mechanical alternans
of blood pressure). In general, electrical and mechanical alternans
seem to occur similtaneously. Alternation is associated with cardiac
instabililty, that is with an increased risk for cardiac rhythm disturbances
(including sudden cardiac death).
- EEG analysis: I've been involved in commercial research seeking
to estimate depth of anesthesia from the EEG.
Sample
Size Selection and Train-Test Set Usage in System Identification
In order to develop parameterized models (e.g., EMG-torque
models), data are required both to train (fit) a model and then separately
to test the model. In many cases, the sample sizes required for training
and testing sets are not easily determined, particularly when iterative
model development occurs. In addition, some model development schemes
encourage the mixing of training and testing sets. I am interested
in investigating model development strategies from collected data sets.
Links to Collaborating
Researchers (Past and Present)
Because EMG amplitude is, by definition, a parameter
of a random process, its value can only be estimated from a sample
of an EMG. The work that collaborators and I have been involved in
is in the development of improved techniques for estimating EMG amplitude.
This work has involved the iterative process of (1) using existing theory
and experimental results to develop an improved stochastic mathematic model
of EMG, (2) based on the improved model, determine mathematically optimal
methods for estimating EMG amplitude (as well as determining an objective
quality measure for the new methods), (3) implementing and experimentally
testing the new estimation technique, and (4) adding these results to the
existing theory.
In general, EMG amplitude estimation from an EMG sample requires six processing steps: (1) noise rejection/filtering, (2) whitening, (3) multiple-channel combination, (4) detection, (5) smoothing, and (6) relinearization. A more complete description of these steps, as well as a review of the present state-of-the-art can be found within the EMG Amplitude Estimation toolbox. Development of EMG amplitude estimation techniques is a continuing research interest.
Relating Surface
EMG Amplitude to Joint Torque
EMG is essentially a by-product of muscle contraction.
The development of muscular tension is the main purpose of contraction.
Hence, it is logical to try to relate the electrical activity of muscle
to its mechanical activity. In general, as the number of active motor
units is increased and/or the average firing rate of active motor units
is increased, both EMG amplitude and total muscle tension increases. However,
the relationship is dynamic and, depending on the resolution desired, may
also need to be treated as non-linear.
It would be ideal, therefore, to relate surface
EMG amplitude to the tension (or, force) produced by individual
muscles. However, there are at least two fundamental difficulties
in doing so. First, classical EMG recorded at the surface of the
skin can contain "cross-talk". That is, EMG from muscles other than
that which the experimenter intends to record may be included in the signal.
Cross-talk is a difficult problem with no immediate, simple solution.
Second, relating EMG to individual muscle tension requires independent
verification via direct mechanical measurement of individual muscle tension.
At present, there is no practical (and perhaps not any) method for
reliably making such measurements.
Because of these fundamental limitations, colleagues
and I have focused our efforts on relating surface EMG amplitude to joint
torque. First, cross-talk, if it exists, may not be as problematic.
Certain cross-talk contributions are automatically removed from the estimated
torque, even if they can not be removed from the individual muscle tension
contributions. Second, net torque about a joint can, in many cases,
be reasonably (or even easily) verified via direct mechanical measurement.
To date, we have examined the EMG-torque relationship
in two simple cases for constant-posture, nonfatiguing contractions about
the elbow. In the first case, slowly force-varying contractions (essentially
no dynamics) were examined and the EMG-torque relationship modeled as a
polynomial relationship. A degree three polynomial (non-linear model)
was found to best describe the relationship. Also, advanced EMG amplitude
estimation algorithms were compared to classical algorithms. The
advanced algorithms gave lower EMG-torque errors. In our second study
case, force-varying contractions were recorded. Linear, dynamic
("black box") system identification techniques were used to relate
EMG amplitude to torque. Again, results indicated that advanced EMG
amplitude estimation leads to lower EMG-torque errors. Relating EMG
amplitude to joint torque is a continuing research interest.
Relating Surface
EMG Amplitude to Joint Impedance
Joint impedance refers to the relationship between
perturbations in joint angle to perturbations in joint torque. That is, if
joint posture is disturbed by applying an external torque about the joint, what
will be the resulting change in joint angle (ignoring adjustments due to
feedback)? Typically, one can decrease the influence of perturbations by
voluntarily increasing impedance via co-activation of antagonists muscles acting
about the joint. Increased impedance is beneficial in many circumstances,
as it serves to reject inevitable external disturbances. However, there
is a metabolic cost to maintaining co-activation, and co-activation increases
the overall workload on the muscles. In many work-related tasks,
constant/frequency muscle activation may be related to cummulative stress
disorders. Thus, we are interested in understanding what mechanical
impedance is generated by various individuals as they perform tasks.
Typically, impedance is measured by applying a
transient force, and then measuring the resulting angle perturbation. In
general, joint impedance is highly non-linear, depending on the type of force
transient applied and the muscle conditions (e.g., joint angle, level of
background muscle activation, fatigue state of the muscle). However, for
small random perturbations applied at one (non-fatigued) muscle condition, the
impedance relationship is well represented as a second-order linear system.
Thus, impedance can be characterized by its stiffness, viscosity and inertia
(which are a function of the "operating point," or muscle condition). For
accurate measurement of impedance, the joint must be perturbed.
In many cases (e.g., ergonomic analysis), an
approximation of the joint impedance would be acceptable, but only if the
impedance could be estimated without perturbing the joint. In this
manner, a worker's impedance could be measure
while performing a task —
and not interrupted by the perturbations. Here, again, surface EMG
amplitude may be useful. Since modulation of impedance is achieved by
modulating muscular effort, we should be able to develop an EMG-impedance
relationship in much the same way that prior researchers have developed an EMG-torque
relationship. At a given operating point, we can measure the agonist and
antagonist EMG amplitude, and the corresponding joint impedance. We can
then relate the EMG amplitudes to joint impedance. We are currently
involving in preliminary work to investigate this relation for conditions which
satisfy the linear second-order model assumptions.
High Resolution EMG Arrays
As noted above, a typical surface EMG signal records
the interference pattern derived from many contributing motor units.
If arrays of small-diameter (≤ 2mm), tightly-spaced (≤ 8mm) EMG
electrodes are used to measure the EMG signal, then weighted combinations
of the recorded signals produce a spatially filtered EMG channel that
can have sufficient resolution to identify individual motor unit
action potentials. There is active research into identifying
optimal spatial filters, electrode array configurations and methods
for using the arrays signals to decompose the EMG signal.
Other EMG-Related Interests
Depending on the opportunity, I'm interested in many other areas of EMG-related
research, including:
- EMG signal changes during sustained (e.g., fatiguing) contractions.
- Use of EMG in clinical applications (neuromuscular assessment,
clinical biomechanics, etc).
Other Biosignal Interests
Other areas of past (and perhaps future) research include:
- ECG and blood pressure analysis: I've studied a phenomenon known
as electrical-mechanical alternans. In electrical alternans, the
shape of the ECG corresponding to alternate heart beats differs.
That is, if the beats are numbered sequentially, all of the odd numbered
beats have one shape and all of the even numbered beats have a second shape.
An analogous sequence occurs in pulsus alternans (mechanical alternans
of blood pressure). In general, electrical and mechanical alternans
seem to occur similtaneously. Alternation is associated with cardiac
instabililty, that is with an increased risk for cardiac rhythm disturbances
(including sudden cardiac death).
- EEG analysis: I've been involved in commercial research seeking
to estimate depth of anesthesia from the EEG.
Sample
Size Selection and Train-Test Set Usage in System Identification
In order to develop parameterized models (e.g., EMG-torque
models), data are required both to train (fit) a model and then separately
to test the model. In many cases, the sample sizes required for training
and testing sets are not easily determined, particularly when iterative
model development occurs. In addition, some model development schemes
encourage the mixing of training and testing sets. I am interested
in investigating model development strategies from collected data sets.
Links to Collaborating
Researchers (Past and Present)
High Resolution EMG Arrays
As noted above, a typical surface EMG signal records
the interference pattern derived from many contributing motor units.
If arrays of small-diameter (≤ 2mm), tightly-spaced (≤ 8mm) EMG
electrodes are used to measure the EMG signal, then weighted combinations
of the recorded signals produce a spatially filtered EMG channel that
can have sufficient resolution to identify individual motor unit
action potentials. There is active research into identifying
optimal spatial filters, electrode array configurations and methods
for using the arrays signals to decompose the EMG signal.
Other EMG-Related Interests
Depending on the opportunity, I'm interested in many other areas of EMG-related
research, including:
- EMG signal changes during sustained (e.g., fatiguing) contractions.
- Use of EMG in clinical applications (neuromuscular assessment,
clinical biomechanics, etc).
Other Biosignal Interests
Other areas of past (and perhaps future) research include:
- ECG and blood pressure analysis: I've studied a phenomenon known
as electrical-mechanical alternans. In electrical alternans, the
shape of the ECG corresponding to alternate heart beats differs.
That is, if the beats are numbered sequentially, all of the odd numbered
beats have one shape and all of the even numbered beats have a second shape.
An analogous sequence occurs in pulsus alternans (mechanical alternans
of blood pressure). In general, electrical and mechanical alternans
seem to occur similtaneously. Alternation is associated with cardiac
instabililty, that is with an increased risk for cardiac rhythm disturbances
(including sudden cardiac death).
- EEG analysis: I've been involved in commercial research seeking
to estimate depth of anesthesia from the EEG.
Sample
Size Selection and Train-Test Set Usage in System Identification
In order to develop parameterized models (e.g., EMG-torque
models), data are required both to train (fit) a model and then separately
to test the model. In many cases, the sample sizes required for training
and testing sets are not easily determined, particularly when iterative
model development occurs. In addition, some model development schemes
encourage the mixing of training and testing sets. I am interested
in investigating model development strategies from collected data sets.
Links to Collaborating
Researchers (Past and Present)
- EMG signal changes during sustained (e.g., fatiguing) contractions.
- Use of EMG in clinical applications (neuromuscular assessment, clinical biomechanics, etc).
Other Biosignal Interests
Other areas of past (and perhaps future) research include:
- ECG and blood pressure analysis: I've studied a phenomenon known
as electrical-mechanical alternans. In electrical alternans, the
shape of the ECG corresponding to alternate heart beats differs.
That is, if the beats are numbered sequentially, all of the odd numbered
beats have one shape and all of the even numbered beats have a second shape.
An analogous sequence occurs in pulsus alternans (mechanical alternans
of blood pressure). In general, electrical and mechanical alternans
seem to occur similtaneously. Alternation is associated with cardiac
instabililty, that is with an increased risk for cardiac rhythm disturbances
(including sudden cardiac death).
- EEG analysis: I've been involved in commercial research seeking
to estimate depth of anesthesia from the EEG.
Sample
Size Selection and Train-Test Set Usage in System Identification
In order to develop parameterized models (e.g., EMG-torque
models), data are required both to train (fit) a model and then separately
to test the model. In many cases, the sample sizes required for training
and testing sets are not easily determined, particularly when iterative
model development occurs. In addition, some model development schemes
encourage the mixing of training and testing sets. I am interested
in investigating model development strategies from collected data sets.
Links to Collaborating
Researchers (Past and Present)
Links to Collaborating Researchers (Past and Present)
| Collaborator | Collaboration Topics |
| Paolo Bonato (Spaulding Hosp/Harvard) | EMG signal processing, rehabilitation, prosthetics |
| Richard J. Cohen (MIT) | ECG signal processing (electrical-mechanical alternans) |
| Kristin Farry (Intelligenta) | EMG signal processing, myoelectric control of prosthesis |
| Gary Kamen (UMass-Amherst) | MU decomposition and interpretation |
| Neville Hogan (MIT) | EMG signal processing, myoelectric control of prosthesis |
| Kevin McGill (Palo Alto VA) | EMG decomposition, EMGlab |
| Roberto Merletti (Politecnico di Torino) | EMG signal processing, instrumentation |
| Denis Rancourt (U. of Sherbrooke) | EMG signal processing, EMG-torque/impedance modeling |
![[L(SP)**2]](image_style/lsp2.jpg "L(SP)**2 Home Page")
![[WPI]](image_style/wpi_logohome.gif)