ME 3901 Engineering Experimentation
Mechanical Engineering Department
Worcester Polytechnic Institute
Temperature Measurements
� Ideal Gas
� Mechanical Effects
� Electrical Effects
� Thermistors
� Thermocouples
� Thermopiles
� Conversions
Temperature Measurements
- Pressure, volume, electrical resistance, expansion coefficients� are all related to temperature through their fundamental molecular structure
- They change with Temperature
- Therefore, they can be used to measure temperature, i.e. they can be surrogates for temperature.
PV = mRT
Take a fixed volume filled with a gas.
Expose it to a known temperature standard and measure the pressure.�
Now expose it to an environment of unknown temperature and measure the pressure.
PuV = mRTu
PsV = mRTs
Pu/Ps = Tu/Ts
Tu = Ts (Pu/Ps)
Using pressure to measure temperature can be accurate to within 1 degree K, especially for very low temperatures.
Consider a typical thermometer
��������� Capillary tube
��������� Alcohol (low temperatures, greater coeff. of expansion)
��������� Mercury (high temperatures)
Error?
��������� Account for expansion of glass surroundings.�
��������� Usually calibrated for a certain depth of immersion.
Bimetallic strip?
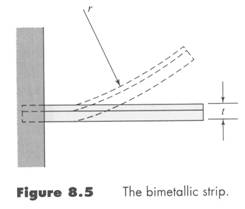
The curvature radius, r, is calculated as:
��������� r = f(expan. coeffs., thicknesses, Es, T, Toriginal_bond)
This device is typical for thermostat applications
Very useful � a signal is produced that is easily detected, amplified, and/or used for control purposes
RTD � Resistance Temperature Detector
Generally, resistance of an element changes with temperature
R = R0(1+aT+bT2)
where R0 is the reference resistance measured at Treference, frequently 0 deg. C.
High grade RTDs use bridge circuits to eliminate lead resistance changes in the same way that strain gages use bridge circuits.
Thermistors � semi-conductor devices.
They have negative temperature coefficients of resistance (whereas most other materials have a positive coefficient)
The behavior follows an exponential variation
R = R0 exp[b(1/T � 1/ T0)]
������ where 3500K < b < 4600K usually
Very consistent and sensitive.� Once calibrated it provides consistent performance within 0.01 oC
Highly nonlinear � not a problem with data acquisition systems.
Thermoelectric Effects (Thermocouples)
��������� � the most common temperature measuring device.
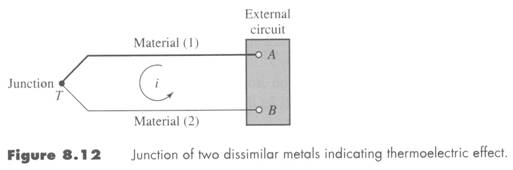
This thermoelectric effect is known as the Seebeck effect.
Certain rules or laws apply for thermocouples (T/C)
1.) if a 3rd metal is connected in a circuit the net emf (voltage) is not affected provided the temperature connections with the 3rd material are the same, law of intermediate metals.
2.) Law of intermediate temperatures � temperatures do NOT add; however, voltages DO add.
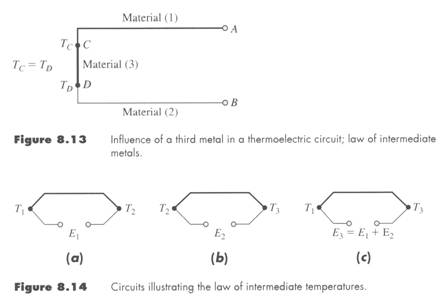
All T/C circuits involve at least two junctions.� If one junction is known, then the other can be calculated.
An ice-bath is very common and accurate reference junction.
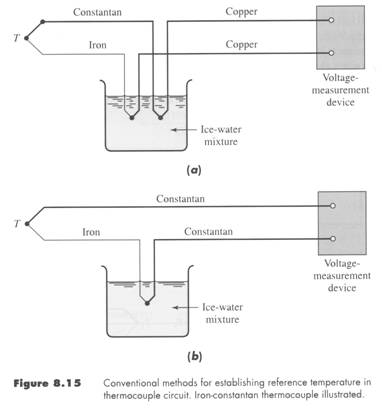
The ice-bath configuration in 8.15a is the best to use.� It does not require the voltage-measuring device (+) and (-) terminals to be at the same temperature.� Figure 8.15b is also fine provided that the voltage-measuring device (+) and (-) terminals are at the same temperature.
An ice-bath reference is ideal.� It is easy to construct and maintain.� Most reference tables are based on a 0oC reference temperature.
This temperature to voltage relationship (in Table 1 from Nat. Instruments) has been expressed in polynomial form such that T = f(V), where T is oC and the voltage is in microVolts.
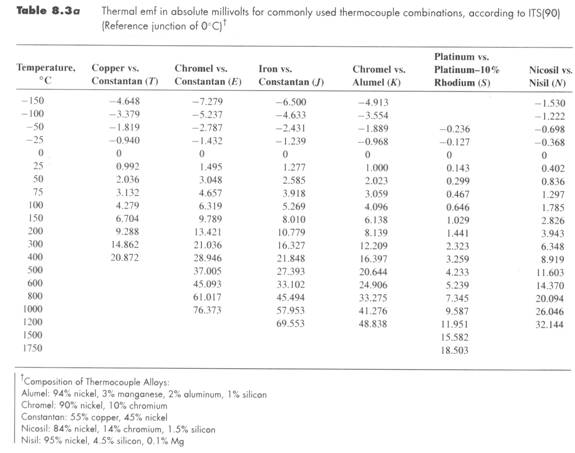
The errors listed in Table 1 are due to the regression coefficients.�
The errors listed in Table 8.3b are due to the material variations of the thermocouple.
This relationship can also be reversed to relate voltage to temperature, i.e. mV = f(T).� Table 2 (from NI) calculates microVolts for a temperature input in oC.
The range of each thermocouple is limited.� The following table (8.17 of Holman) delineates these ranges.� Table 8.3a showed the millivolts output for each T/C type in the given temperature range.� These values can be used to determine which T/C is best for the required application range.
If the millivolts range is too small, or one simply wants a more accurate reading, one can use a thermopile, i.e. add the voltages of each T/C in series to increase the accuracy.�
Note that a thermopile assumes that T1 and T2 are constant.� The averaged voltage generated by the thermopile is used to determine the temperature difference between the two thermal sources.�
This device is frequently used in wind tunnels to report temperature or ventilation ducts and other locations.
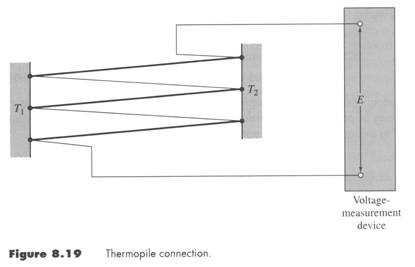
Whether using a thermocouple or thermopile, the voltage generated is a function of the temperature difference between the two junction locations, the thermocouple tip and the voltage card, or the thermocouple tip and the ice-bath junction, or T1 and T2 as in Fig 8.19.
The textbook tables assume a reference temperature, usually 0oC.� Therefore, one must know the temperature of one junction to determine the temperature of the other junction.
Consider the following situation for a type T thermocouple (using Table8.3a):� Assume the Tright is known.
Tleft=75 oC�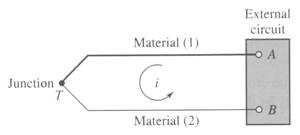 
�Tright = 100 oC
The voltage detected at the external circuit board is -1.147mV.� This value would indicate that the left temperature is lower than the board temperature, Tright.� But the mV value cannot be used directly to calculate the temperature difference.� One needs to know that the board is at 100 oC which would produce 4.279mV relative to a 0oC reference.� This mV value is used to determine that the left side is at (4.279-1.147) 3.132 mV relative to a 0oC reference, which corresponds to a temperature of 75 oC.�
In general one must use Table 2 to convert the known temperature at one junction to a voltage relative to the Table�s reference temperature.� This voltage is added to the �voltage-difference� detected by the voltmeter or potentiometer to establish the voltage of the unknown temperature junction relative to the reference table.� Then use of Table 1 converts the voltage relative to the table to a temperature value.
oF = (9/5) oC + 32.
oR = (9/5) K
K = oC + 273
oR = oF + 459.56
Go to the: [next lecture | chapter top | previous lecture | cover ]
Copyright © J.M. Sullivan, Jr., (2004-2009)
All Rights Reserved.