ME 3901 Engineering Experimentation
Mechanical Engineering Department
Worcester Polytechnic Institute
Summary
· Course Objectives
· Laboratory Experiments
· Calibration
· Error Analysis
· Statistical Analysis of Exp Data
· Temperature Measurements
· Stress Strain Measurements
· Dynamic Measurements
· Summary Statement
Develop experimental (and to a lesser extent analytical and numerical) skills in modern engineering measurement methods.
Develop proficiency in the area of electronic instrumentation and computer-based data acquisition systems.
Laboratories address the practical use of modern devices in actual experiments.
Calibration of Pressure Transducers
Temperature Measurements – T/C, RTD, Thermistor
Force/torque/strain measurements
Resistance measurements
- There are no easy experiments!
- Data acquisition (and control) techniques have advanced rapidly.
- One must know what one is trying to accomplish in order to Design an experiment.
Instrument Capabilities
Bit Resolution
Accuracy à deviation (or error) of reading from a known input
Precision à ability to reproduce a reading (not necessarily correct) from a known input.
Correlate Temperature relative to Voltage
Correlate Temperature relative to Resistance
Correlate Pressure relative to Voltage
Correlate Strain relative to Voltage
Note: Accuracy can be improved up to, But not beyond, the precision of the instrument by calibration.
Three types of error that can cause uncertainty in experimental measurements.
1.) Gross Blunders:
2.) Fixed Errors: Systematic errors, Bias errors – repeated readings to be in error by approximately the same amount, but for some unknown reason(s).
3.) Random Errors: Fluctuations – electronic, personnel, random phenomena frequently statistically distributed; at times difficult to separate from fixed errors
Small systematic errors ~ Accurate.
Small random errors ~ Precise.
How to report error?
Most Results (R) are derived from multiple measurements, R = R(x1, x2, x3, … xN)
(where xi are measured variables), each of which has uncertainty.
Want the uncertainty of the result wr in terms of the uncertainty of the independent wI and dependent, wd measurements.
|
Independent Errors:
Sum ( the squares of the error contributions)
Dependent Errors:
Square (the sum of the errors) ß Much Larger Term
Statistical Analysis of Experimental Data
There are 3 generally accepted definitions of average: the mean, median, and mode.
Arithmetic
Mean: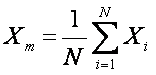 
Deviation: di = Xi - Xm
Standard (root-mean-square) deviation
Population Biased
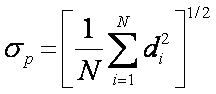
Sample Unbiased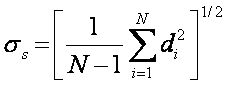 
Generally, if N > 20, then the difference between population and sample standard-deviation values is small and the population statistics can be used.
Median – the ‘Middle’ value of all ranked readings
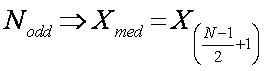
Mode – the ‘most frequent’ value of all readings.
Probability:
A set of data is collected. Do the observations fall within the ‘expected’ values?
A Chi-Squared test is used to answer the question.
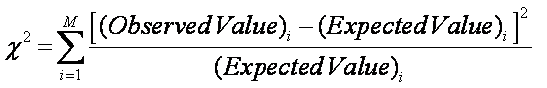
where M = number of groups (not trials). Frequency is used extensively.
Generally, expect: the probability to occur in the range: 0.1< P < 0.9; otherwise, suspect foul data.
Frequently, a parameter has an expected single answer, such as the length of a table top. However, each time one measures it there are slight differences in the length. If sufficient measurements were performed, then a distribution function would result.
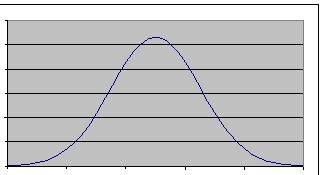
The shape of the distribution function can be ‘normal’, i.e. bell-shaped. The function could be skewed or multi-modal behaviors might exist.
A normal (or Gaussian) distribution gives the probability of a measurement
Generally, the probability that a value will exist within a banded window is expressed in terms of the mean and std. dev.
If the distribution is normal, then 68.3% of the data lie within 1 std dev. Similarly, 95.5% and 99.7% of the data lie within 2 or 3 std dev, respectively.
Chauvenet’s Criterion
A set of data contains some points that “just don’t look right”. However, one cannot eliminate data without having some justifiable cause for the removal of data. Chauvenet’s criterion states that if the probability of occurrence is less than 1/(2N) then the data point(s) can be rejected.
- Pressure, volume, electrical resistance, etc. change with Temperature
- Therefore, they can be used to measure temperature, i.e. they can be surrogates for temperature.
Consider an ideal gas
PV = mRT
Take a fixed volume filled with a gas.
RTD – Resistance Temperature Detector
Generally, resistance of an element changes with temperature
R = R0(1+aT+bT2)
where R0 is the reference resistance measured at Treference,which is frequently at 0 oC.
Thermistors – semi-conductor devices.
The behavior follows an exponential variation
R = R0 exp[b(1/T – 1/ T0)]
where 3500K < b < 4600K usually
Thermocouples
– the most common temperature measuring device.
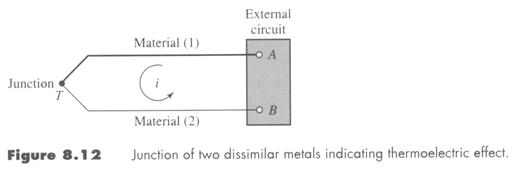
Certain rules or laws apply for thermocouples (T/C)
1.) if a 3rd metal is connected in a circuit the net emf (voltage) is not affected provided the temperature connections with the 3rd material are the same, law of intermediate metals.
2.) Law of intermediate temperatures – temperatures do NOT add; however, voltages DO add.
An ice-bath reference is ideal. It is easy to construct and maintain. Most reference tables are based on a 0oC reference temperature.
Measurement and Analysis
All machines or structural members deform, to some extent, when subjected to external loads or forces.
For Axial Loading:
where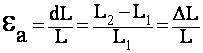 
= Axial
Strain (Len/Len)
L1 = Initial (Linear Dimension) L2 = Final (Strained) Dimension
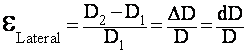
Poisson’s Ratio is defined
as: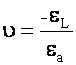 
where 
=
Lateral Strain
Electric – Resistance Strain Gages
- Most widely used method – Resistance changes with Deformation
- Electrical resistance changes with mechanical deformation
Resistance of Conductor
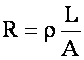where r = resistivity of material
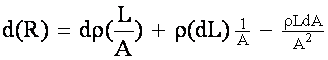
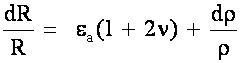
Define Gage
Factor: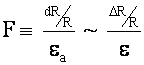 
in Local Vicinity
Then 
Although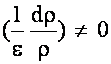 
it IS constant.
Therefore, manufacturers specify the value of F
Then, the local strain can be determined via:
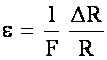
Since F and R are given, à Measure 
and
calculate e
Signal Conditioning is Required.
- most commonly used. It is a purely resistive bridge. It provides a means for accurately measuring resistance and for detecting small changes in resistance.
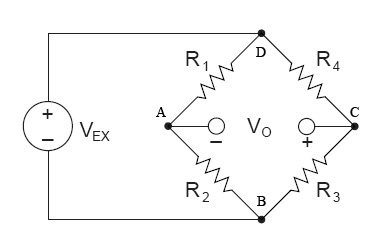
where the voltmeter has negligible current flow.
Voltage read across A and C midpoints
Consider the situation where the Bridge is balanced à Vg = 0
V = I R I1 = I2 and I4 = I3
I1 R1 = I4 R4 and I3 R3 = I2 R2
or
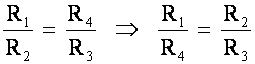
Therefore, Resistance Ratio of any 2 adjacent arms must equal the Resistance ratio of the other 2 arms when taken in the same sense (i.e. L/R or T/B)
Consider a Voltage Divider
Know Vi = I (R1+R2)
Voltmeter (Vo) draws no current
Then Vo = I R1
But I = Vi /(R1+R2)
Therefore Vo = Vi R1/(R1+R2)
à A Voltage Divider
Now
return to the
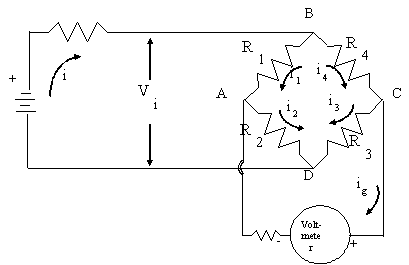
Vo = Vmeter = Vc – Va
let R4 change by a small amount, say (4)
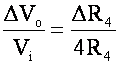
Dynamic Measurements - Vibration:
2nd order differential equation governs the behavior:
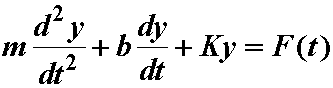
where F(t) is the external forcing function. If the external force is removed then the system is in free vibrational mode and can be described as:
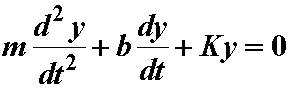
which can be rearranged to:
where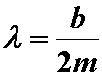 
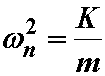
The natural frequency of the beam can be expressed as: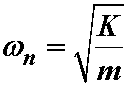 
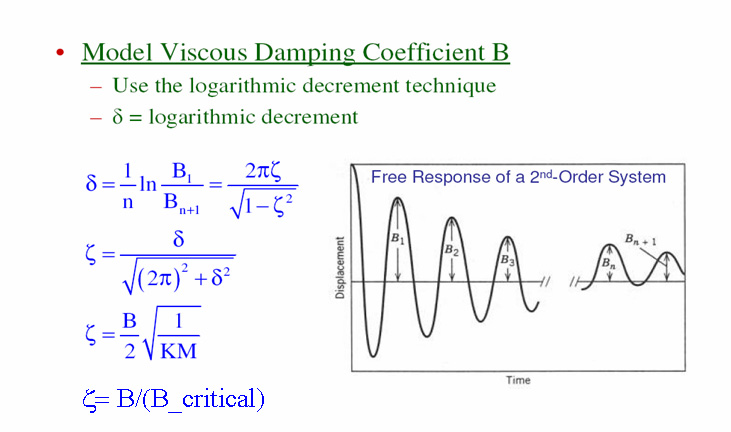
The damping coefficient (b) can be determined based on the logarithmic decrement.
LabVIEW Programming
Panel Design
Diagram Programming
Channel Configurations
Error Analysis
Statistical Analysis
Temperature Measurements
Pressure Measurements
Strain Measurements
Vibration and Dynamic Measurements
Laboratory Reporting Methods and Standards
Congratulations! You’ve acquired significant engineering expertise in experimentation.