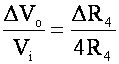ME 3901 Engineering Experimentation
Mechanical Engineering Department
Worcester Polytechnic Institute
Stress and Strain:
Measurement and Analysis
· 1D Stress Analysis
· 2D Stress Analysis
· How to Measure Strain
· Strain Gage Resistance Differentiation
· Commercial Strain Gage
· Whetstone Bridge Analysis
· Voltage Divider
· Whetstone Bridge-Continued
All machines or structural members deform, to some extent, when subjected to external loads or forces.
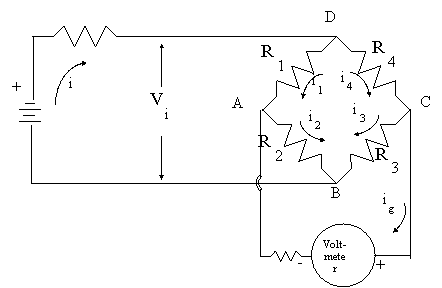
For Axial loading:
 where
where 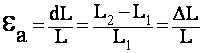
![]() = Axial Strain (Len/Len)
= Axial Strain (Len/Len)
L1 = Initial (Linear Dimension)
L2 = Final (Strained) Linear
Dimension
Frequently, one uses the term
micro-strain or m-strain since the
actual ![]() L is very small
L is very small
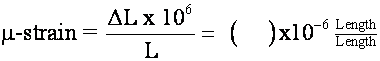
A Stress – Strain relationship for a simple uniaxial load or outer fiber in a beam in bending can be expressed as:
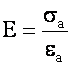 or
or ![]()
where
E
= Young’s
Modulus ![]() = Uniaxial Stress
= Uniaxial Stress
![]() = Strain in direction of Stress
= Strain in direction of Stress
and Poisson’s Ratio is defined as:
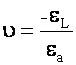 =
Poisson’s Ratio
=
Poisson’s Ratio
![]() =
Lateral Strain
=
Lateral Strain
Consider a small differential element (x1 = y1 = z1 = dx and dv = dx3) subject to
Orthogonal Stresses sx and sy
Initially, only sx is applied
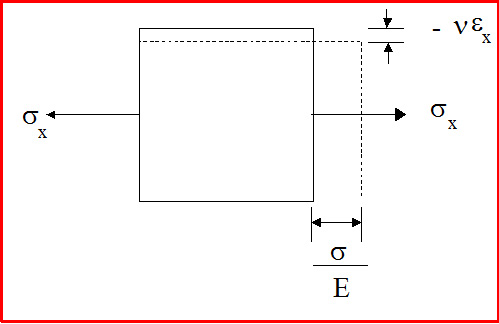
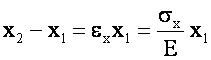
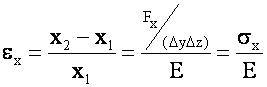

Now apply a stress in the Y direction:
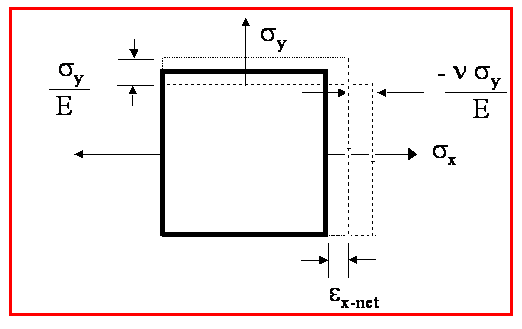
The net strains are:
 and
and 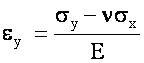
which can be rearranged to:
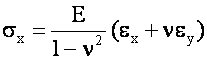
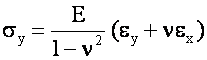
If one applied a stress in the Z direction using the same sequential application:
Photoelastic Coatings Great for concentration
Brittle Coatings points
Grid Methods Requires appreciable
 deformation under loads
deformation under loads
Extensometer (mechanical and optical)
Moire’ (“More Ray”) technique (wavy fringe patterns)
Used for whole-field displacements
Electric – Resistance Strain Gages
- Most widely used method
- Electrical resistance changes with mechanical deformation
A strain measurement must be made over a finite length. (base length).
Deformation Sensitivity – minimum deformation detectable with a gage.
Strain Sensitivity – deformation sensitivity / base length
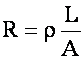 where r = resistivity of
material
where r = resistivity of
material
Differentiating 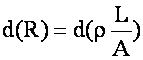
(Simple Product
Rule)
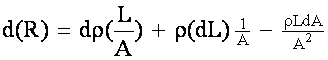
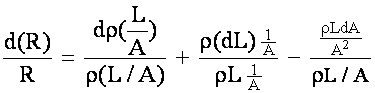
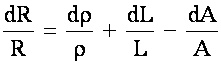
If sample is cylindrical and axial strain only is applied:
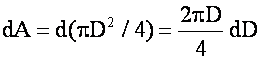
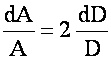
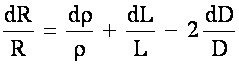
Recall:
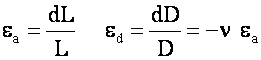
(Poisson’s Ratio 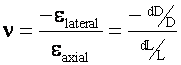 )
)
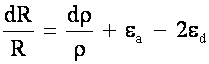
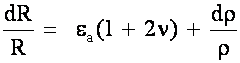
Define: 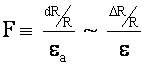 in Local Vicinity
in Local Vicinity
Then
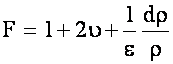
If the quantity 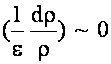 then
F = 1 + 2n
then
F = 1 + 2n
= 1 + 2(0.3)
= 1.6
BUT 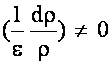 However,
it IS constant over the range of interest.
However,
it IS constant over the range of interest.
Therefore, manufacturers specify the value of F (They experimentally measure F)
Frequently, F ~ 2 (for metal strain gages)
For some silicon based materials F ~ 100
The Manufacturers also specify the strain gage resistance, R
Then, the local strain can be determined via:
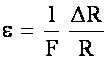
Since F and R are given,
Measure ![]() and then calculate e
and then calculate e
Consider:
F = 2 and R = 120 W
Most commercial strain units can detect a strain
of 1 m-strain
What ![]() causes
this level of strain?
causes
this level of strain?
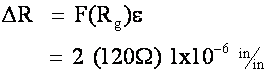
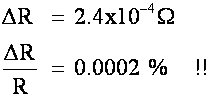
An ohm meter will have trouble detecting this change!
R = 120.00024
National Instruments has additional material for strain gage configurations
Signal Conditioning is Required.
|
most commonly used. It is a purely resistive bridge. It provides a
means for accurately measuring resistance and for detecting small changes in
resistance.
where the meter is a voltmeter – negligible current flow
The bridge is really a pair of voltage divider circuits
D – A – B and D – C – B
Voltage read across A and C midpoints
Consider the situation where the Bridge is balanced
(and Ig = 0)
V = I R
I1 = I2 since Ig = 0
I4 = I3
Also with Vg = 0
I1 R1 = I4 R4 and
I3 R3 = I2 R2
But with I1 = I2 Then I2 R1 = I4 R4
and I4 = I3 I2 R2 = I4 R3
or 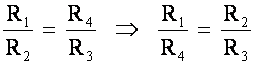
Therefore, Resistance Ratio of any 2 adjacent arms must equal the Resistance ratio of the other 2 arms when taken in the same sense (i.e. L/R or T/B)
|
Know Vi = I (R1+R2)
Voltmeter (Vo) draws no current
Then Vo = I R1
But I = Vi /(R1+R2)
And Vo = Vi R1/(R1+R2) Voltage Divider
Now
return to the
Vo = Vmeter = Vc – Va
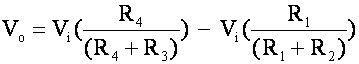
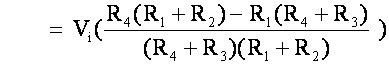
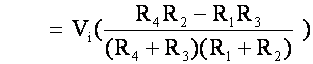
let R4 change by a small amount, say (![]() 4)
4)
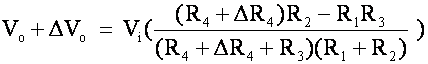
Vo is Zero initially.
Reduce ( assuming R4 = R3) then R1 = R2
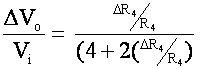
if ![]() <<
1 then 2(
<<
1 then 2(![]() ) << 4
) << 4
and