ME 3901 Engineering Experimentation
Mechanical Engineering Department
Worcester Polytechnic Institute
Error Analysis
· Types of Error
· Least Square Error Analysis
· Uncertainty Analysis for Density
· Hoop Stress Error Analysis
ME3901 is composed of several experiments
Need to learn:
How to measure
What tools/meters to use
The consequences of measurement errors and uncertainty
Data can occur as:
Single measured data – Some uncertainties (meter dependent) may not be discovered by repetition
Ex: Measure fluid T with a thermometer many times. These repeated measurements address the uncertainty in your ability to read the thermometer. But no information is available on the meter itself.
Multi-sampled data – Measure T with several meters/devices
Thermometers
Thermopiles
Thermocouples T/Cs
Thermistors
Three types of error that can cause uncertainty in experimental measurements.
1.)
Gross Blunders:
Construction, Application, Staffing flaws
2.)
Fixed Errors: Systematic
errors, Bias errors – repeated readings to be in error by approximately
the same amount, but for some unknown reason(s). Frequently, the systematic error is quantified as the (Average of the measured readings - True Value). (Unfortunately, the True Value if frequently unknown).
3.)
Random Errors: Fluctuations
– electronic, personnel, random phenomena frequently statistically
distributed; at times difficult to separate from fixed errors. Frequently, the random error is quantified as the (Individual measured reading - Average of all measured readings).
If a measurement has small
systematic errors it is Accurate.
If a measurement has small random errors it is Precise.
Frequently a systematic
error can be mitigated and/or estimated, i.e. calibrate to remove systematic
error
How to report or
‘analyze’ errors?
Common Sense
(variable – who’s common sense!)
Largest error
Worse case error (Sum of all
errors)
It is equally inaccurate to
over-estimate as it is to under-estimate uncertainty.
A
Least Squares Error Analysis
-
Most robust
-
Most widely accepted
Consider
P =
100 kPa
P =
100 kPa +/- 1 kPa
P =
100 kPa +/- 1 kPa (20 to 1)
(This
latter statement requires total lab experience to put odds on uncertainty)
Most Results (R) are derived from multiple measurements, each of which has uncertainty
R = R(x1, x2,
x3, … xN)
where xi are Independent variables
Want the uncertainty of the result wr
In terms of the uncertainty of the independent measurements, wi
That is,
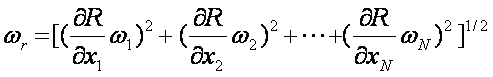
A Least Squares Uncertainty Estimate
Consider the problem –
measure the density, r, of a fluid.
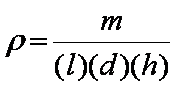
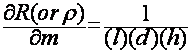
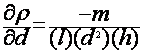

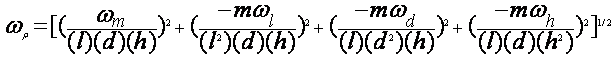
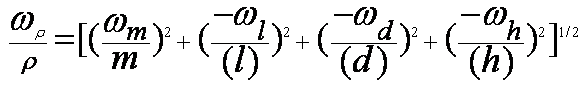
Are these measurements
really independent?
Balance
scale ![]() f(ruler)
f(ruler)
But l, d, and h ARE dependent

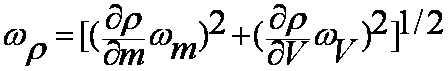

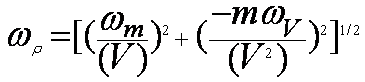
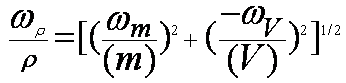
What is the uncertainty in
V?
Let the ruler be ‘shorter’ than actual
then the readings of l, d, and h will all be too large by approximately the same amount
i.e. a Systematic Error
exists
![]()
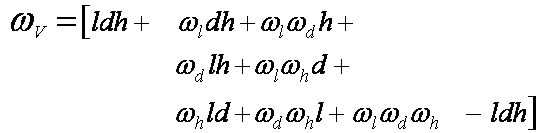
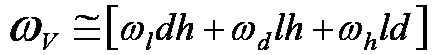
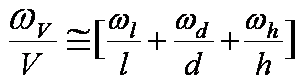
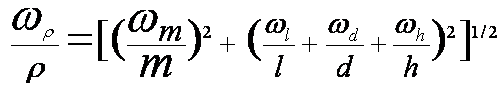
(
Much Larger Term!)
Independent
Errors:
Sum (
the squares of the error contributions)
Dependent
Errors:
Square (the sum of the errors) ß Much Larger
Dependent/Independent Error Conclusions
Dependent Errors cause greater total errors compared to Independent Errors.

Thus, if one had 3
measuring devices (different brand rulers) with similar uncertainties it would
be significantly better to measure the l, d, and h with independent measuring
devices!
This conclusion is contrary
to most peoples’ intuitive experience.
Consider
a measurement of hoop stress from a thin-walled pressure vessel.

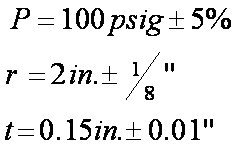
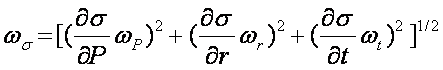
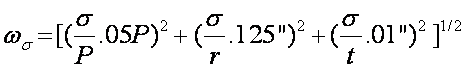
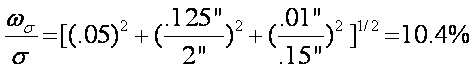
Note:
As with all least square
analyses, a large uncertainty will dominate multiple small uncertainties.
If a single uncertainty is
5-10 times other uncertainties, then stating the resultant uncertainty as the
largest value is reasonable.