Sums over States
Lectures 1-6 presented a demonstration of the powers of classical statistical
mechanics. Our calculations were based on the use of ensembles, an ensemble
being a list of all possible states of the system, together with the
statistical weight assigned to each state. The list of allowed states and
statistical weights is often given implicitly by listing a series of
constraints: for the canonical ensemble, the constraints are fixed N, V, T.
For the 1-atom ideal gas, the states of the system are specified by giving the
position and momentum of the gas molecule. The particle position 
is
allowed to lie anywhere within V, while 
may have any vector value.
The treatment leading to eq. 11.6 masked a fundamental difference between the sums used used in Lectures 8 and 9 and the sums used in all previous Lectures. In the earlier Lectures, the ensemble sum was taken over all states whatsoever of the system. In Lectures 8 and 9, the sum was taken over the system's energy eigenstates. These energy eigenstates are a complete set of states. However, in quantum mechanics, the adjective complete assumes a specific technical meaning, namely that is a set of states is complete if an arbitrary state of the system can written as a sum over the complete set of states. For any system, many allowed states are not included in the complete set of states, namely the mixed states, which are are linear combinations of the complete set of basis states. Note the fundamental difference between the classical and quantum calculations. In the classical calculation, the 'complete' set of states included every single state. In the quantum calculation, the 'complete' set of states included some states but not others.
As an example of the distinction between a complete set of state vectors and a
complete set of basis vectors, consider the model spin system treated above. A
complete set of (basis) states for this system is formed by the energy
eigenstates 
and 
. An alternative complete set of (basis)
states for the system is composed of the helicity states 
and 
. Any other state of the system may be written as a linear combination of
the energy eigenstates or as a linear combination of the helicity states. By
applying Gramm-Schmidt orthonormalization, any non-zero state 
whatsoever of the system may be taken as a basis state; the orthogonality
requirement then determines the other basis state. This is a two-dimensional
system. No matter which (non-zero) state of the system is chosen to be one of
the basis vectors, Gramm-Schmidt orthonormalization will yield two and only two
basis vectors for this system. Since any single state of the system may be
chosen as one of the two basis vectors, there is absolutely no fundamental
physical distinction, without reference to the current choice of basis, in
which any particular set may be said to be `pure'or `mixed'.
While the spin system has only two basis vectors, it has an infinite number of states. Limiting ourselves to normalized states, the complete list of all states of the system, including pure and mixed states, may be written
Here 
and 
are the basis vectors for the system, 
and 
are phase factors ( 
), and 
and
are amplitudes, with 
. There are two basis
vectors, but there are a three-fold infinite set of states of the
system. (In Dirac's formalization of quantum mechanics[1], the
direction but not the magnitude of has physical significance, so the
condition would be lifted.)
If the canonical ensemble includes all states of the system, an average over a
canonical ensemble for the two-level spin should have a sum over all of the
states represented by eq. 11.10, not just a sum (like eqs.
11.5 or 11.9) over a pair of basis states. To write this
average over a canonical ensemble, recognize that an arbitrary state
of the system is characterized by the amplitudes 
and phases 
of its eigenvector components. The pure states are those in which some one
is unity, while the other all vanish. The phases
range freely over the interval 
. The are free to have any
real value, subject to the restriction 
. The
phase factors absorb the sign of ; the amplitudes are restricted to be
positive semidefinite. A sum over all states of a quantum system as opposed to
a sum over a complete set of states, may be expressed
so that the quantum ensemble average becomes
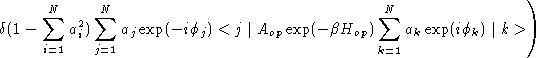
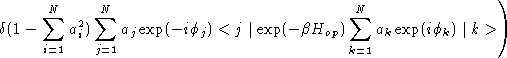
Inspection allows some simplification of these integrals. First extract the
double sum 
to outside the integrals. Each term of the
double sum contains a factor
Nothing outside this factor, e.g., E, should depend on or
. The self terms of the double sum yield factors 
. The
distinct terms of the double sum vanish, reducing the double sum to a single
sum, namely
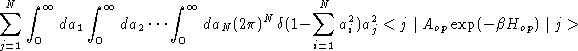
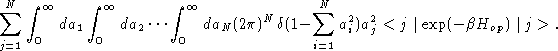
The integrals in eq. 11.14 need not be evaluated explicitly. The
quantum averages 
and 
depend on J but not on the 
.
Except for the label j, the integrals
are the same in every term of the numerator sum and in every term of the denominator sum. Substituting eq. 11.15 into eq. 11.14,
While complicated in structure, the factors 
above and below are
constants, which may be cancelled, giving
for the ensemble average and
for the partition function. An ensemble average over all states of a
quantum system thus reduces to an ensemble average over a complete set of basis
states. Eq. 11.18 justifies our claim
above that the partition function can be written as a sum over energy
eigenstates. It is important to emphasize that the results of this section
have nothing to do with the results of the previous section. In the previous
section, we showed that 
is independent of the choice
of basis set. In this section, we showed that computing
over any choice of basis set gives the same result as
computing over all states of the system.
