References

1

P. A. M. Dirac, Quantum Mechanics Oxford U. P. (1958).

2

There is the significant difficulty that in most cases the number N of basis vectors needed to form a complete set is not finite. If N is infinite, the integrals of eq. 11.14 diverge; the proposed cancellation is meaningless. This difficulty can apparently be circumvented by taking N to be the number of basis vectors in a finite subspace of the system's Hilbert space, demonstrating the cancellation, and then taking the limit 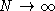. As N goes to infinity, the error in approximating any state vector 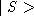as a sum of a subset of the set of all basis vectors will vanish.

3

The alert student may remember that Planck's derivation of the black-body radiation formula, which appears to use energy quantization, dates to 1901. T. Kuhn, The Black Body Paradox...?, U. Chicago Press discusses in careful detail what Planck appears to have thought he was doing. In particular, Planck in 1901 appears to have viewed both the field and the oscillator sources as having continuous values for their energy, the use of a sum over quanta being a clever device (borrowed from Boltzmann's use of the same combinatorial arguments) for avoiding a phase-space integral. Only after Jeans' 1903 paper could it easily have been recognized that Planck did not obtain the expected classical result. The `ultraviolet catastrophe' described in many undergraduate texts as a motivating force for Planck's work was unknown until Jeans' calculation was published, and Jeans published his work after Planck did. [Rayleigh's work refers to sound and ether waves, not to electromagnetic waves described by Maxwell's equations.] Only in 1906 did Einstein point out that Planck's 1901 calculation was incorrect -- or at least did not match Planck's description of it -- in that Planck's energy quantization condition 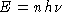was not a clever mathematical trick for approximating an integral, but instead a physical assumption that changed the final result of the calculation.