Norm of a Vector or Signal
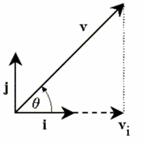
A vector and one of its
components.
The norm is equivalent to the magnitude or the length of a vector squared. The norm of a signal is the integral of the signal squared. This is also known as the energy of the signal. Now, part of the benefits of using i and j as a basis set for vectors is that they are unit vectors. Since the length of each vector is unity, it makes it easier to express the component in the i-direction of v in terms of i. For instance, if we want to express vi in terms of i, then vi is simply |vi|∙i, since |i| = 1. We say that the basis vectors i and j have been normalized.
How do you normalize a vector or signal if it is not originally normalized? Basically you divide it by its own length. In the case of geometric vectors such as u = 3i + 4j and v = i + 2j – 2 k , they have norms of 5 and 3, respectively (the reader is urged to check this by squaring the components, adding the results up and taking the square root). Thus the normalized versions are, respectively,
and 
(the mark over each vector of ^ is traditionally used to indicate a normalized vector).
In the signal world, a signal is normalized by taking the inner product of the signal with itself. The inner product for a signal is the integral of the signal squared which is also the energy of that signal. When calculating the c coefficient we must normalize the signal by dividing by the energy.
![[WPI]](http://www.wpi.edu/Buttons/seal.gif){kind=small}
***
Discovery Project II. Vaz, Richard F. 2001. WPI.
<http://www.ece.wpi.edu/courses/ee2311/temp/dp2.htm>