ME 515 - Computational Methods for Partial Differential Equations
in Engineering and Science
Lecture #1: How to Classify PDEs and
Determine IF the Problem is Well Posed?
let t, x, y, z be independent variables
and u, v, w be dependent variables
i.e. u = u(t,x,y,z) with partial derivatives denoted as:
 |
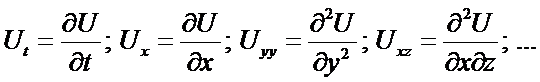Examples of equations involving partial derivatives used in engineering are:
U =
Uxx + Uyy + Uzz = 0
(Uxx + Uyy + Uzz ) = f(x,y,z) Poisson’s Equation
Ut = D (Uxx + Uyy + Uzz) Diffusion Equation
Wave
Equation
U
+ lU = 0 Helmholtz
Equation
Utt + aUt + bU = c2 Uxx Telegraph Equation
Difference between a PDE and an ODE
Consider a 1st order, quasi-linear, ordinary differential equation:
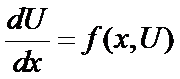
One specifies x and U —> f and get a unique slope value dU/dx.
Alternately, examine a first order quasilinear PDE
 |
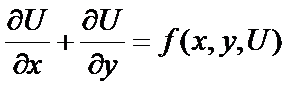If one specifies x, y, and U a relation between Ux and Uy is obtained.
Unique values of each are not available.
In general, a point, plane, or tangent line for an ODE corresponds to a curve, 3-D space, and tangent plane for a PDE, respectively. The increased dimension is a direct result of the increase in independent variables.
How do we solve PDEs ?
Separation of Variables
Similarity Transformations
Method of Characteristics PDE --> ODE
Transform Techniques
Green's Functions
Unfortunately, any of the following (frequently occurring physical phenomena) items eliminates analytical solutions of the PDE
Nonlinearities, Irregular boundaries, Inhomogeneous
Conditions, Anisotropy, Complicated Forcing Functions
Therefore, we must recognize what type of PDE is being solved and whether the problem statement is well posed.
Much is known about linear PDEs and this information is cataloged according to the form of the PDE.
All linear 2nd order PDEs in 2 independent variables can be converted into one of three standard or CANONICAL forms at a point, wherein, at least 1 of the 2nd order derivatives is absent.
Consider the following general form of a 2nd order PDE
aUxx + bUxy + cUyy + dUx + eUy + fU = 0 (1)
Lump and move all terms of order less than two over to the right hand side as “h”
 |
The 3 Canonical forms are:
b2 - 4ac > 0 ----> Hyperbolic - 2 characteristic curves
b2 - 4ac = 0 ----> Parabolic - 1 characteristic curve
b2 - 4ac < 0 ----> Elliptic - no real roots
Physically, these forms are propagation (Hyper & Para), equilibrium and eigenvalue problems (latter two being elliptic)
Given that the PDE is classified, one must recognize the boundary condition requirements for a well posed problem.
Boundary conditions are classified as:
Dirichlet, Type I, Essential U is given
Neumann, Type II, Natural ðU/ðn is given
Robbins, Type III, Mixed f = f(U, ðU/ðn) is given
Cauchy - Both slope and value are given.
Hyperbolic equations have Cauchy conditions in an open region
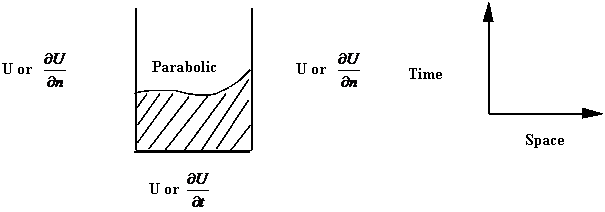
Parabolic equations have Dirichlet or Neumann conditions in an open region.
Elliptic equations have Dirichlet or Neumann conditions in a closed region.
Summary
1.) First Step: Examine the PDE and classify in Canonical form.
2.) Determine if B.C.s are appropriate or over/under specified.
3.) If problem is well posed, seek help from analytical solutions cataloged in Canonical form.
*********************************
Supplemental material
Examples:
A) Separation of Variables
Most common method for solving initial-boundary value problems
Let Eq (1) be homogeneous with constant coefficients, i.e.
aUxx + bUxy + cUyy + dUx + eUy + fU = 0 (3)
Assume
U(x,y) = X(x) * Y(y) ¹ 0 (4)
Substituting (4) into (3)
aX’’Y + bX’Y’ + cXY’’ + dX’Y + eXY’ + fXY = 0 (5)
Dividing (5) by (aXY) with a < > 0
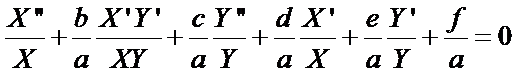(6)
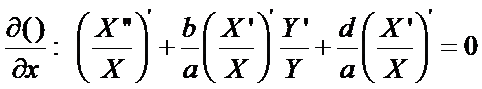
(7)
Equation (7) is separated so that both sides are equal to a constant, say l
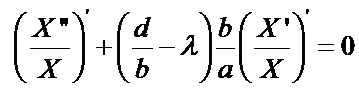(9)
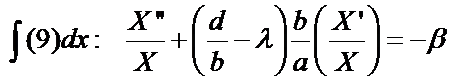
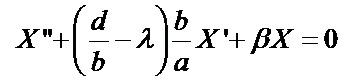S.O.L.D.E.
Constant of
Integration: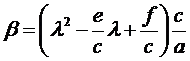 
B) Similarity Transformations:
Consider a 1-D transient heat problem into a semi-infinite domain.
The governing equation is
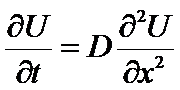
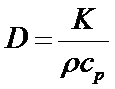
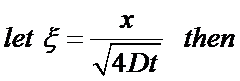
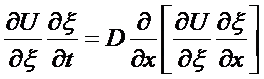
where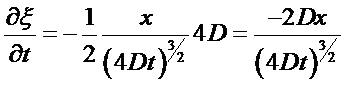 
and 
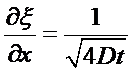
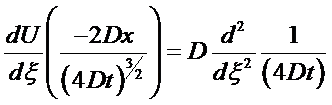or
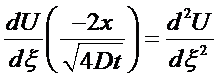
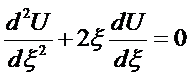S.O.L.D.E.
Go to the: [Next Lecture | Lecture Top | Previous Lecture ]
Copyright © J.M. Sullivan, Jr., (2004, 2005, 2006).
All Rights Reserved.