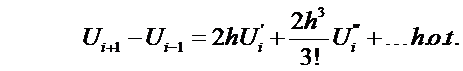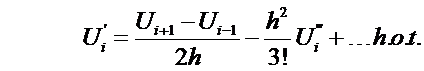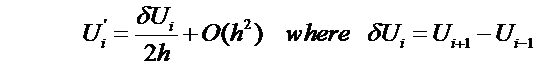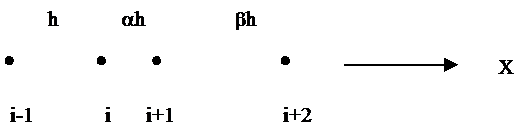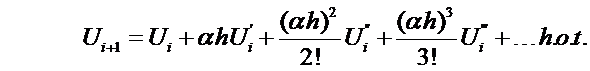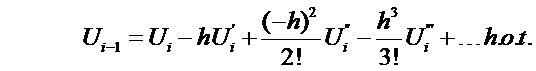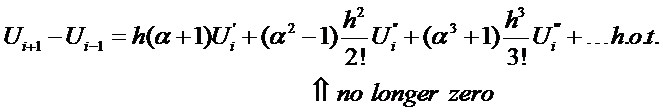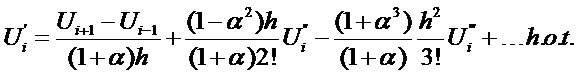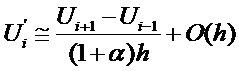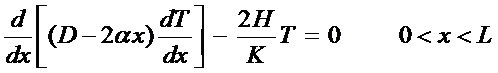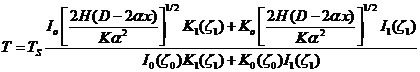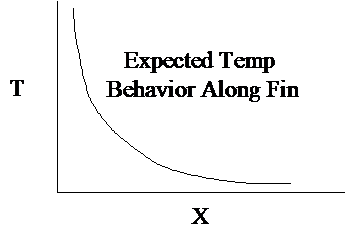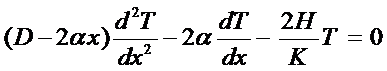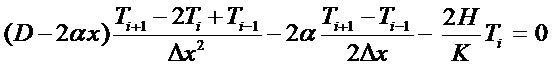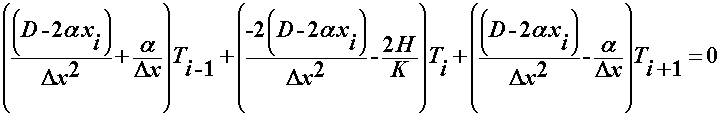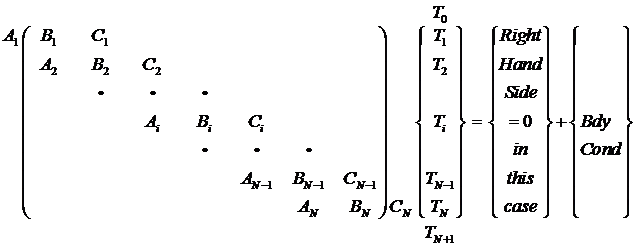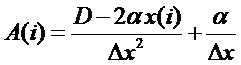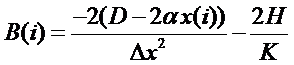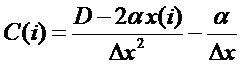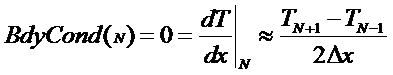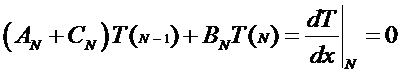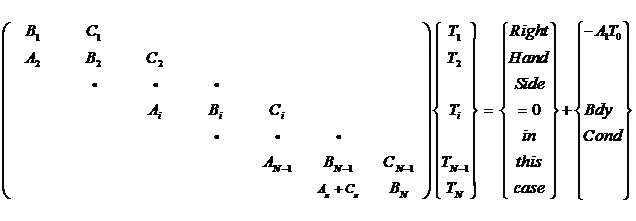Last time:
a) Classify PDE in
canonical form
b) Determine if
given B.C.’s make the problem well posed
c) Examine
analytical solutions ‘surrounding’ physical problem for comparison with
numerical solutions throughout physical problem.
Today: Finite Difference
Calculus
When a function U and its derivatives are single-valued,
finite and continuous functions of x then by
Taylor’s theorem:
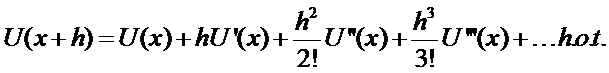
or
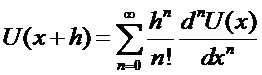
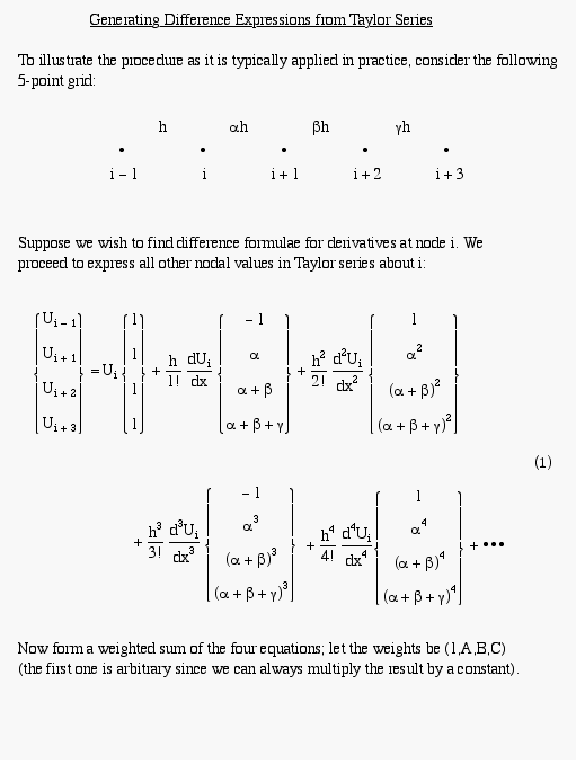
Consider a 1-D situation with nodes uniformly
spaced
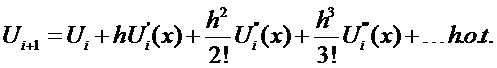
Rearrange
for 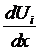
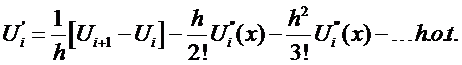
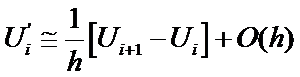
This is a first
order approximation since the leading error term
is of the ‘order’ h ~ O(h)
The
finite difference literature defines 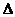 to be the forward difference operator, i.e.
to be the forward difference operator, i.e. 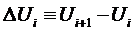 so that:
so that:
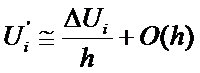
A
second order derivative can be found in
similar fashion:
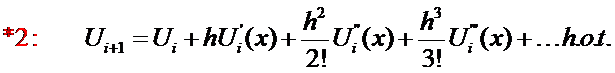

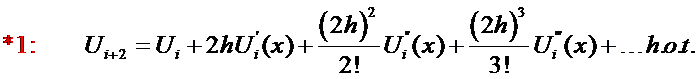
We want to solve for  in terms of
in terms of  . Therefore, we must
eliminate
. Therefore, we must
eliminate 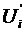 from the above equations. Multiply Eqn (6) by two and subtract from Eqn
(7):
from the above equations. Multiply Eqn (6) by two and subtract from Eqn
(7):
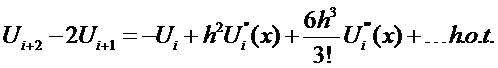
Rearrange for 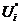
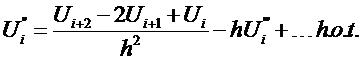
or 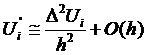 where
where 
Generalizations:
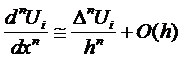 and
and 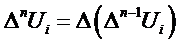
That
is:
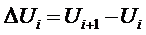
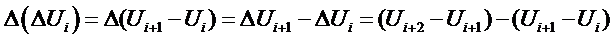
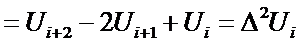
n+1
points are required to represent 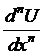 with a leading error
term of O(h)
with a leading error
term of O(h)
Suppose
one wishes more accuracy, i.e. 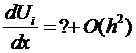
Write
out the
Taylor
series:
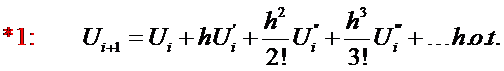
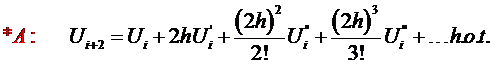
We
must eliminate 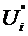 to represent
to represent 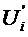 with O(h2)
accuracy.
with O(h2)
accuracy.
Multiply
Eqn(11) by A and add to Eqn(10).
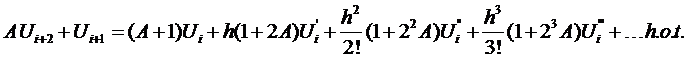
To
remove  the quantity (1+4A) =
0. That is, A = -1/4
the quantity (1+4A) =
0. That is, A = -1/4
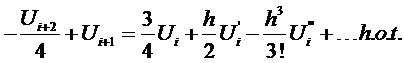
Rearrange
for 
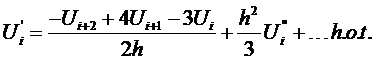
or
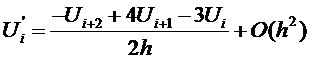
In
general, n+m points are required to represent 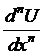 with a leading error
term of O(hm)
with a leading error
term of O(hm)
There
is no restriction that one must use forward finite difference
approximations. We can describe 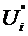 via
via
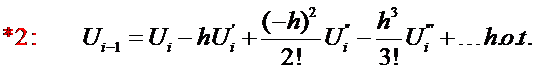 (16)
(16)
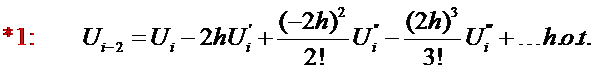 (17)
(17)
Multiply
Eqn (16) by 2 and subtract from (17)
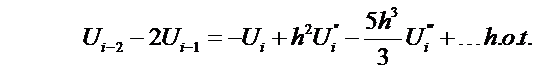
Rearrange for 
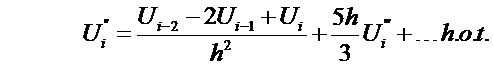
or
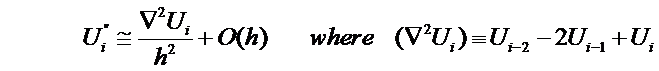
Similarly,
examine using a forward AND backward
finite difference expressions
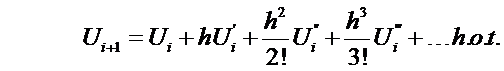 (18)
(18)
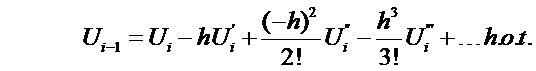 (19)
(19)
Subtract Eqn (19) from (18):
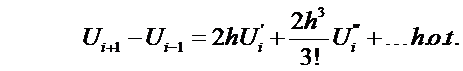
Rearrange
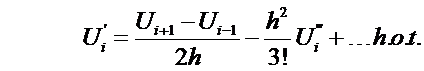
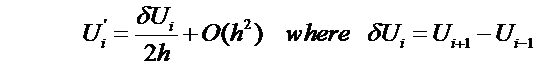
Note that for the same number of nodes, the central
finite difference formulation is an order of magnitude more accurate.
Uniformly Spaced Finite
Difference Coefficients (Taken from Hornbeck reference)
Consider what happens when the node spacing is not
uniform
Examine the central difference formulation
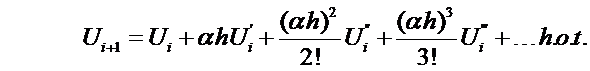
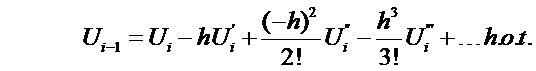
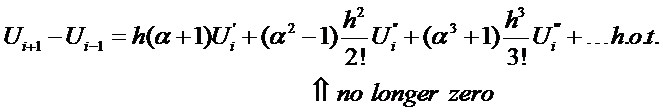
In general: Loose an order of accuracy when mesh spacing
is variable!
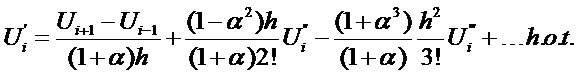
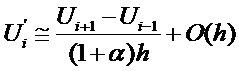
and the complexity of the
formulation increases rapidly
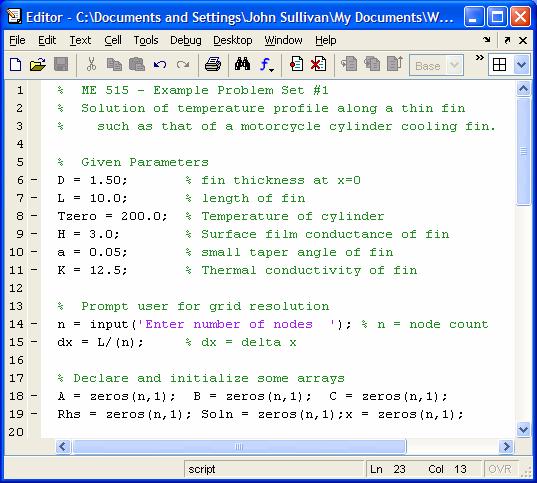
Example: Consider the heat transfer in a thin,
slightly tapered fin attached to a chamber. The fin cools the chamber by radiation or forced convection, i.e. a
motorcycle cylinder fin. Since the fin
is thin, the temperature across its thickness is assumed constant. Determine the steady state temperature
profile along the fin subject to the following boundary conditions.

T = Ts
at x
= 0
where
Ts = Tcylinder
dT/dx = 0
at x = L
The following 1-D O.D.E. can
be used to describe this situation (Carslaw & Jaeger, pg 142)
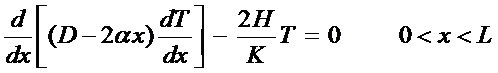
Where
D is the thickness of the fin at x=0
a is the small angle of taper of the fin
K is the thermal conductivity of the fin
H is the surface conductivity of the fin
L is the length of the fin
The analytical solution for
this problem is:
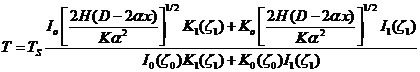
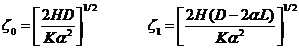
Where I0, K0,
I1, K1 are modified Bessel functions.
The complexity is due to the
coefficient (D-2ax)
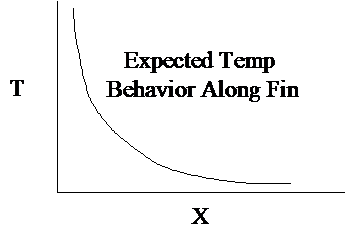 However, a tapered fin is standard in Engineering
Designs.
However, a tapered fin is standard in Engineering
Designs.
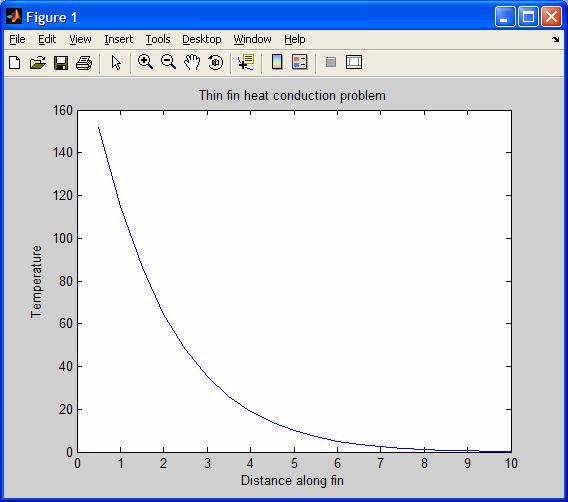
And we would expect the
temperature profile to drop along the length of the fin.
How do we solve this system
numerically?
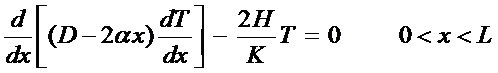
Rewrite the O.D.E as:
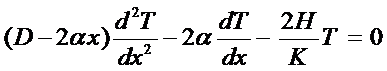
Replace the continuous
derivatives with the central finite difference approximations. Return to the Hornbeck tables and fill in the
nodal subscripts.
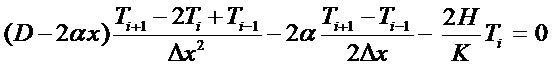
Discretize the domain
Where Dx is constant.
Rearrange finite difference
expression
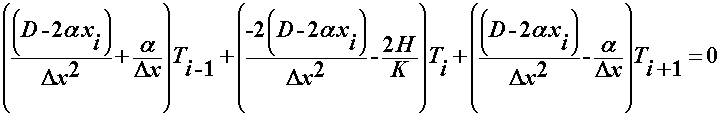
For i = 1, 2, … n
This system of unknown
equations requires a tri-diagonal matrix solver, i.e. the Thomas algorithm.
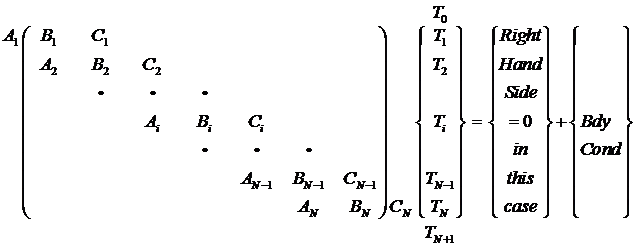
Where:
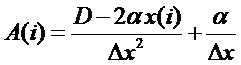
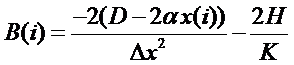
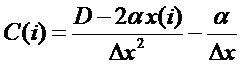
There are N equations and N
unknowns, so it can be solved. Need to
apply the boundary conditions.
At node 1 (Not the boundary):
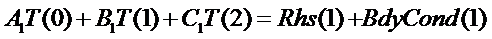
But T(0) = Ts =
known value, and
BdyCond(1)=0
since node 1 is not a boundary node
Therefore move the A1T(0)
to rhs which partially cleans up the lhs matrix:
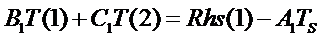
Examine the equation at node
N, which is a boundary node.
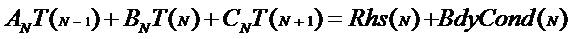
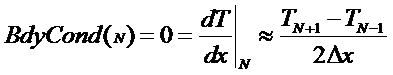
This formulation gives us an
expression for the imaginary or shadow node (N+1). That is: T(N+1) = T(N-1) for the boundary
condition to be true.
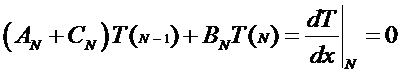
Now the lhs matrix has been
corrected and the system of equations can be solved!
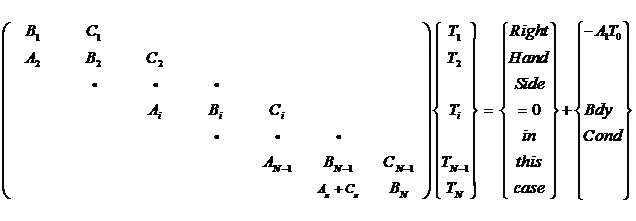
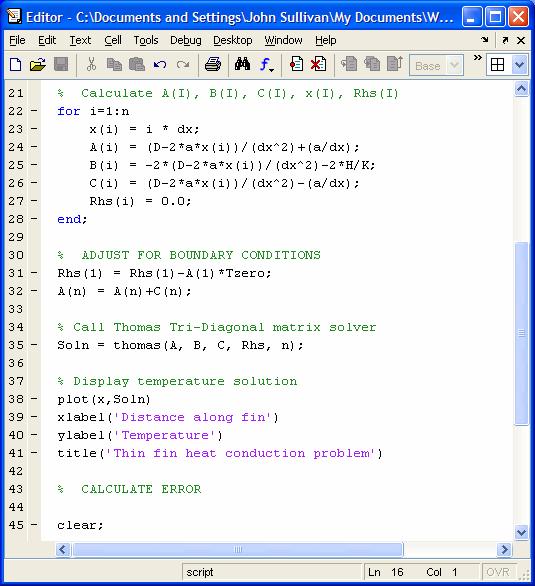
To solve, Calculate A(I),
B(I), C(I), X(I), Rhs(I)
Adjust for the Boundary
Conditions:
Rhs(1)
= Rhs(1) – A(1)*TS
A(N)
= A(N)+C(N)
Rhs(N)
= Rhs(N) + BC(N) = 0 in this case.
Call
a tri-diagonal matrix solver, such as Thomas’ routine
Soln
= Thomas(A, B, C, Rhs, N)
The
temperature solution returns in the Soln(I=1 to N) array.
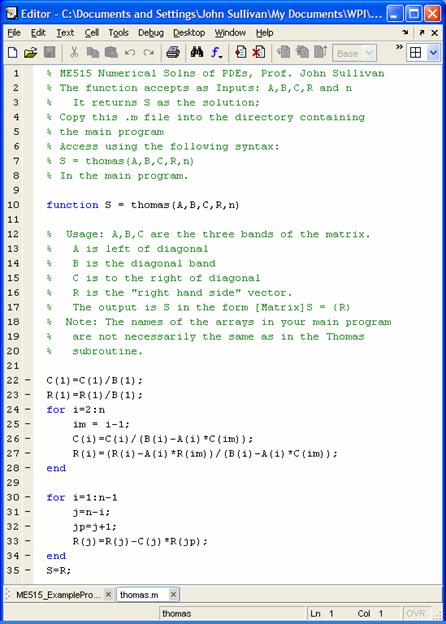
This tri-diagonal solver is
incredibly efficient and short (only about 14 lines of code).
% ME515 Numerical Solns of
PDEs, Prof. John Sullivan
% The function accepts as
Inputs: A,B,C,R and n
% It returns S as the solution;
% Copy this .m file into the
directory containing
% the main program
% Access using the following
syntax:
% S = thomas(A,B,C,R,n)
% In the main program.
function S =
thomas(A,B,C,R,n)
% Usage: A,B,C are the three bands of the
matrix.
% A is left of diagonal
% B is the diagonal band
% C is to the right of diagonal
% R is the "right hand side" vector.
% The output is S in the form [Matrix]S = {R}
% Note: The names of the arrays in your main
program
% are not necessarily the same as in the Thomas
% subroutine.
C(1)=C(1)/B(1);
R(1)=R(1)/B(1);
for i=2:n
im = i-1;
C(i)=C(i)/(B(i)-A(i)*C(im));
R(i)=(R(i)-A(i)*R(im))/(B(i)-A(i)*C(im));
end
for i=1:n-1
j=n-i;
jp=j+1;
R(j)=R(j)-C(j)*R(jp);
end
S=R;
How
do we create a code to model this situation?
What
are the basic, fundamental components of a code?
Copyright © J.M. Sullivan, Jr., (2004, 2005, 2006).
All Rights Reserved.
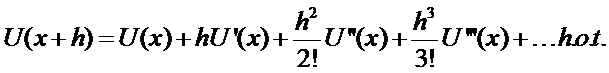
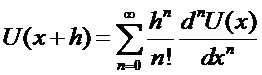
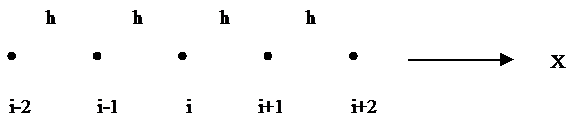
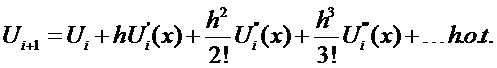
![]()
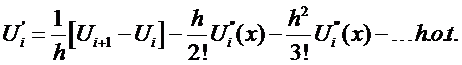
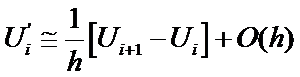
![]() to be the forward difference operator, i.e.
to be the forward difference operator, i.e. ![]() so that:
so that: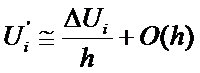
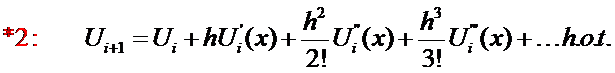
![]()
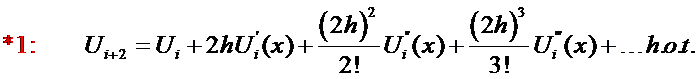
![]() in terms of
in terms of ![]() . Therefore, we must
eliminate
. Therefore, we must
eliminate ![]() from the above equations. Multiply Eqn (6) by two and subtract from Eqn
(7):
from the above equations. Multiply Eqn (6) by two and subtract from Eqn
(7):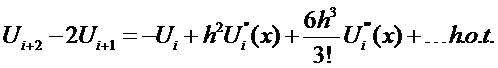
![]()
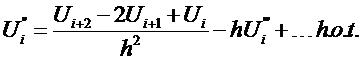
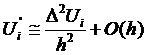 where
where ![]()
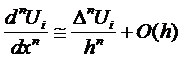 and
and ![]()
![]()
![]()
![]()
![]() with a leading error
term of O(h)
with a leading error
term of O(h)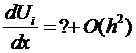
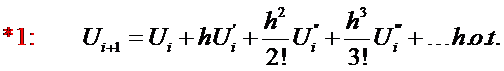
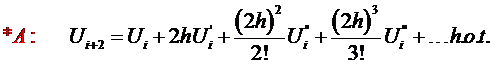
![]() to represent
to represent ![]() with O(h2)
accuracy.
with O(h2)
accuracy.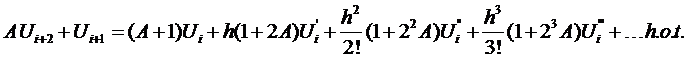
![]() the quantity (1+4A) =
0. That is, A = -1/4
the quantity (1+4A) =
0. That is, A = -1/4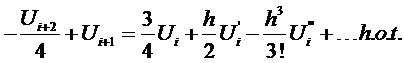
![]()
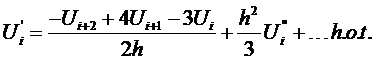
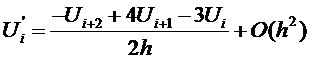
![]() with a leading error
term of O(hm)
with a leading error
term of O(hm)![]() via
via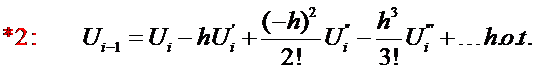 (16)
(16)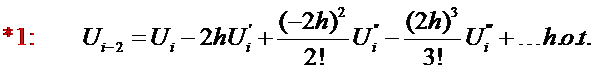 (17)
(17)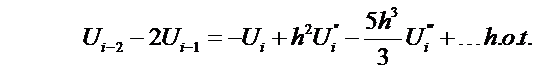
![]()
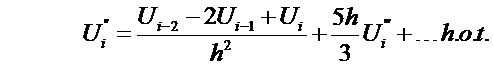
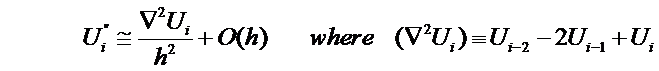
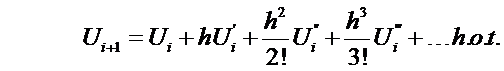 (18)
(18)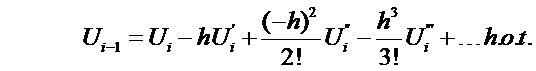 (19)
(19)