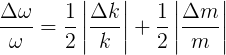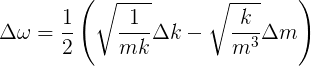
In many cases, such as this one, we get compact, easy-to-remember expressions by dividing Δω by ω itself (obtaining thereby something called the FRACTIONAL UNCERTAINTY). From the relationship ω = √(k/m), we obtain
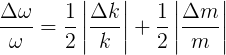
In this third experiment with the mass-spring system, you will be repeating a few now-familiar steps, but mostly you will be learning something new about handling uncertainties, about curve fitting, and about the relative phases among the four measured quantities; Fx(t), x(t), vx(t), and ax(t). Again, there are two parts to this experiment: Part 1 involving mass and spring constant measurements, the theoretical prediction of the angular frequency of a mass-spring oscillator, complete with uncertainty; and Part 2 involving the actual measurements of Fx(t), x(t), vx(t), and ax(t) during 10 seconds worth of oscillations so that you can determine experimentally the angular frequency of oscillation, and other system parameters such as relative phases and the relationships among amplitudes.
So far this must sound too familiar—even redundant. Today we will consider a topic ignored in our work so far: Is our assumption that the spring is massless correct? Can we make a correction to perhaps improve the comparison of the values for the angular frequency determined from our force constant measurements and those found by a curve fit to sine wave created when the spring oscillates? Does this effort provide a better comparison between Theory and Experiment?
Please make use of the Data Sheet and the Report found below to help you clarify how to perform this experiment.
Today you will continue working with mass-spring system. This time all of your work will be done with a single spring so that you can more easily focus on other aspects of the behavior of the mass-spring oscillator.
Your station should be prepared with all appropriate Vernier sensors and a container of masses. Please be certain to have two springs one rather skinny and the other relatively fatter.
First measure the mass of the spring, the mass hanger, and the slotted masses on one of the mass balances available in your lab room. After you measure the mass of the spring (about 6g, fat spring, ~4g, skinny one), measure the mass of the hanger-plus-50-g-slotted-mass combination, and then add additional masses in 100-g increments, measuring the total mass each time, until you reach a total of 600g. The total mass at each measurement should be within half of an integer number of 100g units—if it is not, ask your lab instructor for a properly-sized replacement mass. Record the spring mass on your data sheet for future reference. (Later you can use half a gram as the slotted mass uncertainty, unless you measured deviations from stated values consistently and substantially less than half a gram in magnitude.) Notice that we are attempting to be more precise today with our measurments.
Now complete the necessary measurements to determine the force constant, k, as you have done before.
Now that you have measured masses and determined the spring constant in order to predict the angular frequency of subsequent oscillation (complete with uncertainty), the next step is to put a mass/spring system into oscillation so that you can compare the measured angular frequency of oscillation with the theoretically-predicted value, as well as to make measurements of the relative phases.
Open the Logger Pro File for Part 2. Reduce the mass hanging from the spring to 300g (total mass 303 ± 3g, counting the spring mass). With the mass hanger motionless, zero the force sensors, and then set the system into oscillation by pulling the mass hanger down about 1 to 1.5 cm from equilibrium and releasing it. When you are satisfied, begin collecting data (which automatically ends after 10 seconds), and, if necessary, autoscale the data.
All four graphs are sinusoidal in nature, so we're going to employ a different fitting routine than the usual linear fit in order to quickly extract system parameters from these graphs. This Logger Pro file is automatically set up to fit each curve with a sinusoid, and then provide a data box superimposed on each graphical region listing the respective amplitudes (A), angular frequency (B), and the phase (C), (and the vertical zero-offset (D) which you will never use in this experiment).
First, look at the parameters shown in each data box labeled B. B is the angular frequency of oscillator. All 4 boxes should have essentially the same ω value, all with incredibly tiny uncertainties. Record that best-fit ω value on your Data Sheet for later comparison with theory.
Now click on the Data tool bar button, and "Clear All Data". Change the total mass hanging from the spring to 400g, damp out its motion at equilibrium, zero the Sensors, put the system in oscillation with a 1 to 1.5 cm amplitude as before and collect 10 seconds of Fx(t), x(t), vx(t), and ax(t) data. As before, the data display on the Logger Pro template will include the sinusoidal fitting parameters "A", "B", and "C". Record all three values on your Data Sheet for subsequent comparisons with theory.
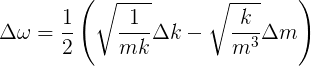
In many cases, such as this one, we get compact, easy-to-remember expressions by dividing Δω by ω itself (obtaining thereby something called the FRACTIONAL UNCERTAINTY). From the relationship ω = √(k/m), we obtain