PH 1120 Lab 3: Electric Potential and RC Circuits

Overview

There is still one more property of electric potential, namely potential difference, that you will work through because it is so directly relevant to lecture discussions about the electric potential. Due to the fact that the electrostatic field is a conservative field, the potential difference encountered in moving from one point to another depends only on the location of the end points and not on the path followed from start to finish. Add to that the fact that electric potential is a scalar quantity, potential difference promises to be easy to work with. There is one complication, and that is the fact that charge polarity must be taken into account because charges come in positive and negative varieties.

Another important property is capacitance, or the ability of an object to hold an electrical charge. A capacitor is an important electrical component that can hold separated amounts of positive and negative charges. Capacitors are as common in many electrical circuits as resistors. One important task to learn is the set of rules for determining the equivalent capacitance of a set of individual capacitors in parallel and/or series arrangements with one another.

Part 1: Electric Potential

Calculate the potential at a +1 point charge (1.00) and at a second point one grid length directly away with a +0.5 charge (0.50). Now, calculate the potential difference associated with moving from the first point to the second. Remember that a potential difference between two points is always defined to be Vfinal – Vinitial [Page 762, 13th edition of Young and Freedman].

Part 2: RC Discharge

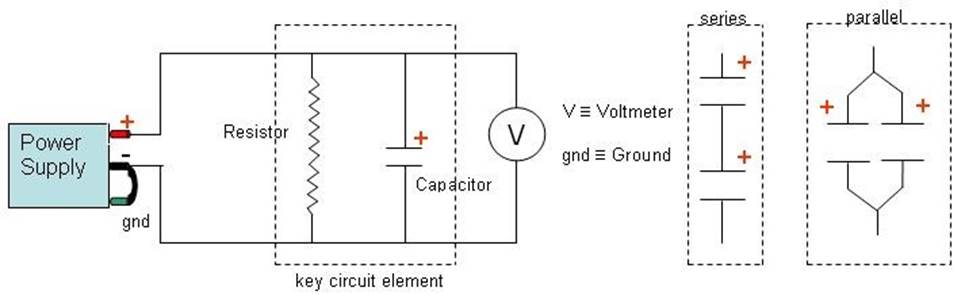
The resistance of carbon resistors is relatively easy to measure, as you learned in the previous experiment, the direct measurement of capacitance requires special equipment that we are not going to duplicate at some 30 separate PH 1120 lab stations. You are going to use a special approach especially suited to our Vernier equipment, with the emphasis on measuring the equivalent capacitance value of parallel and series combinations of capacitors as discussed in lecture. Note that the voltmeter is connect "across" the capacitor; it is in parallel with the capacitor.

Circuit diagram for lab 3.

As you will hear in lecture, a charged capacitor connected to a resistor discharges through the resistor in such a way that the voltage across the capacitor decreases with time according to the equation

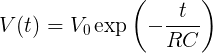
The electric potential

where V0 is the initial voltage across the capacitor at time t=0, R is the resistance value of the resistor, and C is the capacitance value of the capacitor. LoggerPro is able to plot both V(t) and ln(|V(t)|) = a – t/(RC) for some constant a.

Whereas V(t) is an exponential, the natural log of the absolute value of V(t) is a straight line of slope magnitude

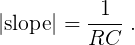
The electric potential

You will be using an R = 22,000 Ω ± 5% resistor in this experiment, and you will be measuring the slope of the natural log of the time-varying voltage across the capacitor, which means that you can solve for C as

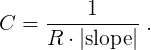
The electric potential

Here is the procedure to follow:

  1. Hook up the circuit with only one capacitor connected in the circuit as described by your Lab Instructor. BE SURE to connect the capacitor into the circuit properly with the + end (if the capacitor has a polarization preference) connected to the positive side of the voltage supply. Open the RC LoggerPro template, and turn on the power supply (making sure that the voltage control knob is turned CCW all the way to its zero position). Now, zero the reading and then turn up the voltage of the power supply until the voltage meter reads about 5.0 V.
  2. Start collecting data and quickly prepare to disconnect the + voltage clip lead from the circuit once the "Collect" button turns red and you see data begin to collect, forming horizontal lines on the graph. As soon as you disconnect the + voltage, the capacitor will begin to discharge through the resistor, and you will see the two voltage graphs being recorded suddenly change profiles- one following an exponential profile with time, while the other follows a downward-sloped straight line. Data collection automatically stops after 10 seconds. You should turn down the voltage supply to 0 at this point.
  3. Highlight from near the top of the downward-sloped straight line to a point where that graph begins getting noisy, and perform a least-squares fit. When the "Select Columns" dialog box opens deselect the "Latest Potential" choice so that only straight-line graph will be involved when you close the dialog box. Then right click the least-squares data box so that you can select the "Linear Fit Options" where you will select 5 significant figures and "Show Uncertainty." Write down your slope magnitude and uncertainty values (See Note Below). The reciprocal of the quantity "slope magnitude" times 22,000 Ω gives the value of the capacitor in farads (F), the SI unit for capacitance. Note: What you should do for uncertainty in capacitance is simply to calculate the 4 capacitance values, using the slope magnitudes and 22,000 Ω. Take 5% of each resultant as the uncertainty, and then express each capacitance value in industry-standard format.
  4. Now repeat the experiment with the first capacitor replaced by the second capacitor found at your station, then both in parallel, and finally with both in series. Be careful to connect the positive side of the capacitor (if polarized) to the positive side of the voltage supply and zero the reading (with the voltage supply still at zero) between each experiment.

Logger Pro Files and Lab Report

Back to PH 1120 Labs

Back to Main Page