PH 1120 Lab 2: Electric Potential and Determining Resistance

Objectives

Background

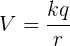
Equipotential surfaces are imaginary surfaces used to visualize areas around a charge where the electric potential is equal. Consider a point charge, with an electric potential around it calculated using the equation

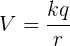
The electric potential

The electric potential around a point charge will be equal at every point that is the same distance r away from the charge. Therefore equipotential surfaces around a point charge take the form of spherical shells. Consider whether two different equipotential surfaces can ever intersect. Note that electric potential is a scalar—it is represented only in terms of a number (which may be positive or negative), but not a direction.

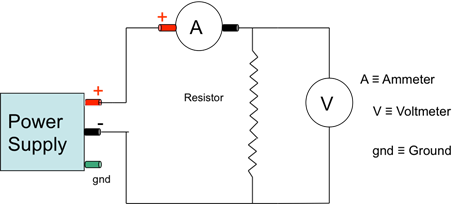
Electric potential is also used when measuring properties of electric circuits. Connecting a voltmeter (in parallel) to two points in a circuit will yield a measurement of the potential between those two points. It should be noted that voltmeters (and ammeters) are directional. Depending on which way the voltmeter is connected, it can read a positive or negative value for the difference in potential.

Batteries are rated in terms of voltage: in a 9 volt battery, for example, the difference in potential between the positive terminal and negative terminal is approximately 9 volts. It is this difference in potential that causes charge to flow through a circuit when the battery is connected.

Ohm's Law is an important relationship in circuitry used to relate the potential (V), current (I), and resistance (R) between two points. It is expressed by the equation

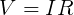
The electric potential

In general, circuit potential (voltage) is measured in units of volts (V); current is measured in amperes, or amps (A); and resistance is measured in ohms (Ω). Ohm's Law does not always hold, but carbon resistors have the property that their resistance stays constant across a wide range of currents. Therefore the resistance of a carbon resistor can be calculated by plotting a chart of current by voltage and finding the slope.

The best way to find the value of a calculable quantity (like resistance in this case) is to take many measurements and find their average and standard deviation. In some cases one measurement is a decent approximation for the true value, but in other cases the measurement error is large and multiple measurements are needed.

Pre-Lab Procedure

Answer the first two questions in the worksheet regarding equipotential surfaces. Recall that electric potential is a scalar, and equipotential surfaces are contours along which the electric potential does not change. Later in the lab, we will be measuring the potential difference across a resistor using a voltmeter.

Lab Procedure

Circuit diagram for lab 2.

  1. Build the circuit according to the following diagram. Use either the 51Ω or 68Ω resistor, and note that the voltmeter is connected in parallel with the resistor, while the ammeter is connected in series.
  2. Make sure the power supply is set to zero, and zero the reading in Logger Pro. Record nine data points, each at a different voltage in half-volt increments. If the voltage does not increase when the knob is turned, make sure the current limit knob is set to about the middle of its range. Never exceed 6V across the voltmeter or 0.6A through the ammeter. This can damage the equipment.
  3. Your data should be a straight line with slope equal to the resistance of the resistor in Ohms (R = V/I). Fit this to a line in Logger Pro. Make sure to save both the slope value and the uncertainty in your worksheet.
  4. Repeat steps 2 and 3 three more times using the same resistor, for a total of four resistance values and their associated uncertainties.
  5. Use the Excel sheet to calculate the average and standard deviation for the resistance values. Record these values in your worksheet and use them in further calculations for questions 4 and 5.

Logger Pro Files and Lab Report

Back to PH 1120 Labs

Back to Main Page