Trigonometry

Trigonometry takes on two distinct forms:

• right triangle trig
• oscillating function trig

Each one plays a huge role in basic physics, calculus and engineering

right triangle trig: force diagrams, geometry, vector analysis

oscillating functions: calculus, mass-spring systems, circuits, sound,

and any vibrations such as musical notes.

Contents:

1. Right Triangle Trig

1.1 Pythagorean Theorem

1.2 SOH CAH TOA and similar triangles

1.3 Trig values for 0°, 30°,45°,60°, and 90°

1.4 Degrees and Radians

1.5 Trig Identities

2. Oscillating Functions

2.1 basics of sine and cosine

2.2 Amplitude, Frequency and Phase Shift

1. Right Triangle Trigonometry

1.1 The Pythagorean Theorem

The Pythagorean Theorem is the cornerstone of trigonometry and analytic geometry. It relates the lengths of the sides of right triangles. First you need to remember the terminology:

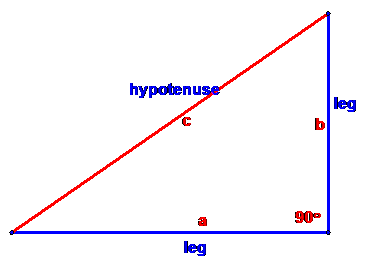
If we denote the lengths of the three sides by a and b for the legs and c for the hypotenuse, then in a flat plane the Pythagorean Theorem states that

c² = a² + b²

The most widely known right triangle is perhaps the “3-4-5” triangle shown below

where we note that 3² + 4² = 9 + 16 = 25 = 5². Other right triangles with integer sides are 5-12-13 and 20-21-29. The reader should check that the two sets of numbers really do satisfy the Pythagorean Theorem.

Skill: Completing the Triangle

One thing that one should be able to do is as follows: given two sides of a right triangle, be able to fill in the length of the third side. This is called “completing the triangle”.

Example 1: Complete the following triangle

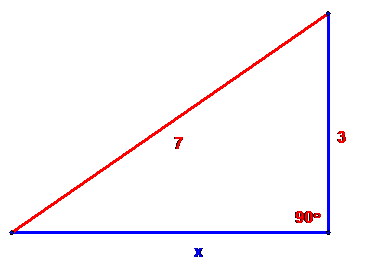
Solution: we must have x² + 3² = 7²

or x² + 9 = 49

or x² = 49 – 9 = 40

so x =

(most problems result in a square root appearing somewhere…)

Example 2: Complete the following triangle

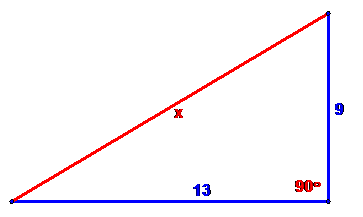
Solution: We need to determine the hypotenuse this time. We have

9² + 13² = x²

or 81 + 169 = x²

or 250 = x²

so x =

Problem: why is it true that a + b > c ??

Problem Set #1

1. Complete each right triangle below where two of the three sides are given, with the first being the hypotenuse

a) 75, 60

b) 58, 40

c) 39 ,15

d) 100, 60

e) 65,56

f) 85,84

2. In each problem below, the three sides of a triangle are given. Decide if it is a right triangle or not

a) 5, 10, 15

b) 20 ,21, 29

c) 20, 50, 52

d) 1 , 1, √2

e) 4,5, 9

f) 12,35,37

g) 11,60,61

Follow this link for solutions to Problem Set #1

1.2 SOH CAH TOA

If one of the angles (not the 90 degree one) are denoted by θ and we distinguish the legs as to being adjacent to the angle or opposite it then the triangle looks like

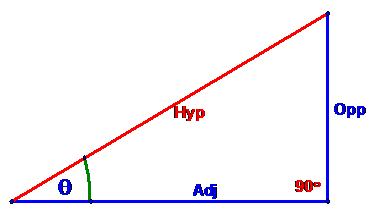
The Pythagorean Theorem in this case states

Hyp² = Adj² + Opp²

The basic trig functions are defined as ratios of the sides of the triangle as the legs relate to θ (either adjacent to it or opposite it).

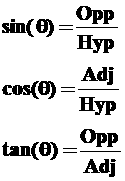
You need to memorize these!!! They are pronounced:

sin(θ) = “sine theta”

cos(θ) = “cosine theta”

tan(θ) = “tangent theta”

For the right triangle shown below, we would then have

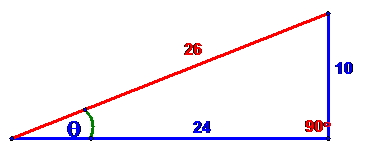
that sin(θ) = 10/26 = 5/13,

cos(θ) = 24/26 = 12/13

and tan(θ) = 10/24 = 5/12.

Sometimes you have to complete the triangle first before you can figure out the values of the trig functions as shown by the following example

Example For the triangle shown below, determine sin(θ), cos(θ) and tan(θ).

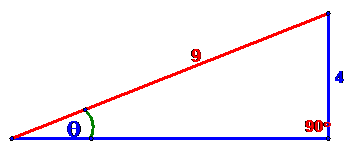
Solution: step 1 – complete the triangle

the adjacent side is found by solving x² + 4² = 9² or x² = 81 – 16 =65 so

x =

step 2 – read off the trig values

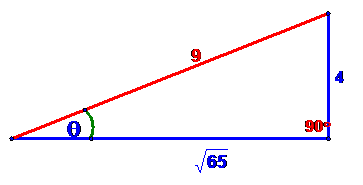
so that

that sin(θ) = 4/9

cos(θ) = /9

and tan(θ) = 4/

Complementary Angles

It is well known that for any triangle, the sum of all three angles is always 180°.

Now for a right triangle, one of those angles is 90°, so the other two angles add up to 90°. They are called complementary because of this. Thus if you have a right triangle and you know one angle, you really know all three. If, for example, one angle is 37 degrees than the other must be 63 degrees and the triangle might look like

Knowing this and SOH CAH TOA can save us some work. We start with the following triangle and base what follows on it:

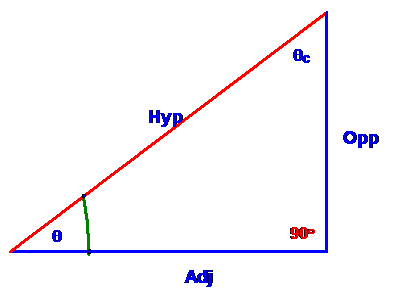
Now, remembering SOH CAH TOA, we can write down all of the following:

sin(θ) = Opp/Hyp

cos(θ) = Adj/ Hyp

as well as (check this)

sin(θ_c) = Adj/Hyp

cos(θ_c) = Opp/Hyp

because of where θ_c is located on the triangle. Putting this together,

cos(θ_c) = sin(θ) and sin(θ_c) = cos(θ)

or, equivalently

sin(θ) = cos(90° - θ)

or, put verbally: if you know sine of an angle then you know cosine of its complement, and if you know cosine of an angle, you know sine of its complement.

For example, if we are given that sin(40°) = .643 then we automatically know that cos(60°) = .643 .

If we know that cos(55°) = .82 then we know from this that sin(35°) = .82.

Part of geometry and, in particular trigonometry, is getting all the possible mileage you can out of the given information in a problem…. deductive reasoning.

Problem Set #2

1. Given are the three sides of a right triangle. If θ denotes the angle between the first side given and the hypotenuse, sketch the triangle and determine sin(θ), cos(θ), and tan(θ). Leave your answer in fraction form

a) 8,6, 10

b) 2, 3, √13

c) 5,5, √50

d) 12,5,13

2. Given are the two legs of a right triangle. . If θ denotes the angle between the first side given and the hypotenuse, sketch the triangle and determine sin(θ), cos(θ), and tan(θ). Leave your answer in fraction form

a) 2,5

b) 1,4

c) 15, 36

d) 21,20

e) 3, 3

3) In each case, cos(θ) is given. Deduce as much additional information from this as you can. Feel free to use a calculator

a) .3

b) .5

c) .866

d) .81

Follow this link to solutions to Problem Set #2

1.3 Trig values for 0°, 30°,45°,60°, and 90°

You will frequently need to know the values of sine, cosine and tangent for the angles listed above. What follows will try to cut down on the amount of memorization and also explain where the values come from. For starters, we will focus only on sine and cosine and then fall back on the fact that tan(θ) = sin(θ)/ cos(θ).

Our goal is to fill in the following table based on what we know:

θ	sin(θ)	cos(θ)
0°
30°
45°
60°
90°

45° is a good place to begin. The triangle may look like

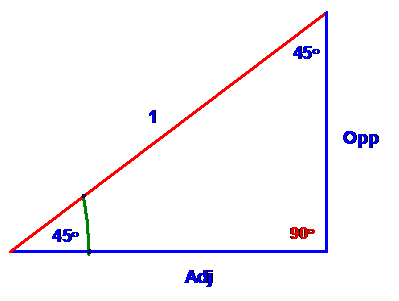
if we make the hypotenuse 1. Note the second 45° because they have to add up to 90°. This makes the triangle isosceles and hence Opp = Adj . By the Pythagorean Theorem, we then have

1² = Adj² + Opp² = Adj² + Adj² = 2Adj²

so Adj² = ½ and therefore Adj =

Therefore the triangle looks like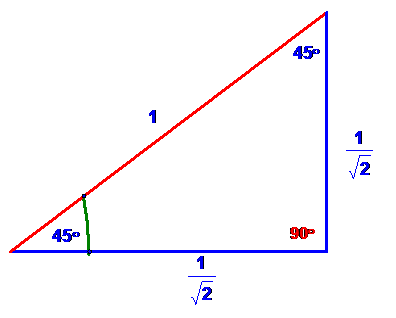

and thus cos(45°)= sin(45°)= .

The table now looks like

θ	sin(θ)	cos(θ)
0°
30°
45°
60°
90°

Let’s set up an equilateral ^*triangle with sides 1 unit long:

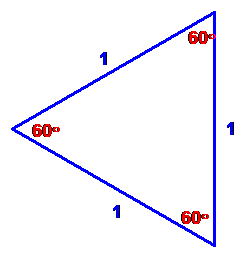
*equilateral means that all three sides are the same length. Isosceles means two equal sides

Now, you point out, this is not a right triangle and we were doing trigonometry, the study of right triangles. True… but let’s add a line from the left vertex to the midpoint of the vertical side. Now things look like

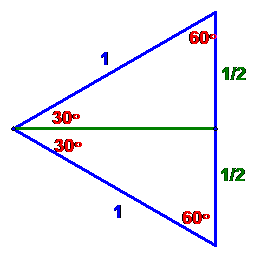
and we note that the green, horizontal line is perpendicular to the vertical, blue line. We have created two, congruent, right triangles, called “30-60-90” triangles. We have 2 of the three sides of each. If we let x denote the length of the green, horizontal side then one of them looks like

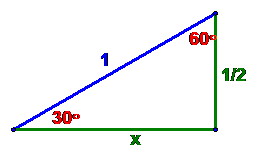
where, from the Pythagorean Theorem, we have x² + (1/2)² = 1² so x =

and the triangle, completed, is

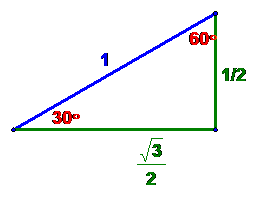
From SOH CAH TOA, we get sin(30°)= = cos(60°) and cos(30°) = = sin(60°)

The table now looks like

θ	sin(θ)	cos(θ)
0°
30°
45°
60°
90°

and we note that because of the property of complementary angles discussed earlier, every time we determine 2 trig values, we effectively get 2 more free of charge. Thus if we can figure out sin and cosine of 0° we are really done.

For 0° we can start with a very, very slim triangle with hypotenuse of 1. This might appear as

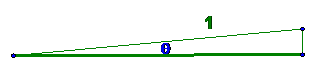
Remembering that sine is opposite divided by 1 and cosine is adjacent divided by 1, we then imagine θ getting smaller and smaller and becoming 0. The adjacent and the hypotenuse both become the same thing so cos(0°) = 1.

By similar thinking, the opposite side becomes 0 as the angle collapses, so sin(0°) = 0.

The table now looks like

θ	sin(θ)	cos(θ)
0°	0	1
30°
45°
60°
90°

For 90 degrees the role of sine and cosine are reversed so we can fill in the last row as

θ	sin(θ)	cos(θ)
0°	0	1
30°
45°
60°
90°	1	0

The property of complementary angles has saved us half the work. It can save you half of the memorization by the following pattern of duplication of values (indicated by corresponding colors):

θ	sin(θ)	cos(θ)
0°	0	1
30°
45°
60°
90°	1	0

where each pairing occurs for the simple reason that sin(θ) = cos(90° - θ)

Completing Right Triangles Using Trig Functions

This is a skill where, given only the hypotenuse and an angle in a right triangle, one can fill in all three sides of the triangle.

For example, consider the following problem:

Problem: determine all three sides of the triangle shown:

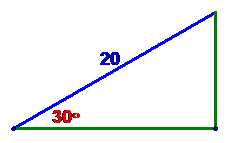
Solution:

Let’s find the adjacent (horizontal) side first. Call it’s value x. Then by definition, the ratio of adjacent to hypotenuse is the cosine of 30 degrees, or

cos(30°) = x/20

=

so

To next find the opposite (vertical) side, we have two ways to do it: use the Pythagorean Theorem or use trig functions as we just did. We’ll go with the latter to illustrate it as you already know how to use the Pythagorean Theorem

Call this unknown side y. Then by definition (recall SOH CAH TOA)

sin(30°) = y/20

= 1/2

so y = 20(1/2) = 10

The triangle, now completed, looks like

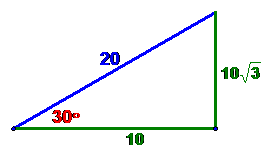
Another approach: we developed the trig values for 30 degrees using a triangle with a hypotenuse of 1 unit and adjacent angle of 30. What we needed in this problem was a triangle 20 times as big and similar (in the mathematical sense) to the original so we just multiply or scale all three sides by 20 and we are done

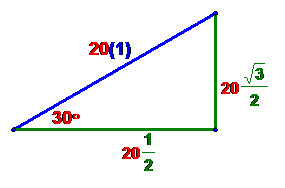
Comment: to do these kinds of problems , you need to know SOH CAH TOA cold as well as the values from the trig table. There is no way around this.

Problem: complete the following triangle

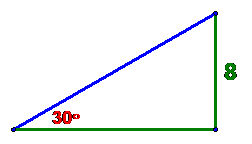
Solution:

let’s get the hypotenuse first. Call it H. By definition

sin(30) = 8/H

We know sin(30) = ½ so ½ = 8/H or H = 8/(1/2) = 16

To get the horizontal side, which we call A, we know that

cos(30) = A/H = A/16

and, from the table, that cos(30) = so

A/16 =

and A = 16 = 8

The completed triangle now looks like

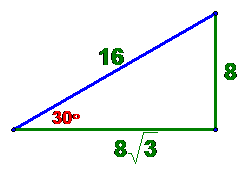
Comment: we can check our work by seeing if our three sides satisfy the Pythagorean Theorem. If not, we made a mistake. In this problem,

so we are ok.

Problem: complete the following triangle

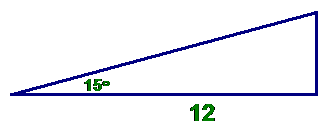
Solution:

let’s call the vertical side y and the hypotenuse h. Then we are looking for values to complete

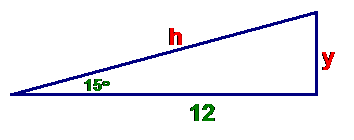
Let’s find h first. By definition, cos(15°) = 12/h so h = 12/cos(15). To finish, we need the cosine of 15 degrees which requires a calculator. This tells us cos(15°) is about .966 so

h = 12/.966 = 12.42

We now have two out of three sides. We can get y either with the Pythagorean Theorem or Trig functions. We will show both

Pythagorean Theorem:

h² = y² + 12²

(12.423)² = y² + 144

154.34 = y² + 144

10.34 = y²

3.22 = y

Trig functions:

sin(15°) = y/h = y/12.42

but sin(15°) = .259

so y = 12.42 * .259 = 3.21

The “completed” triangle now looks like

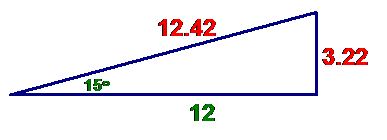
Since decimals were used, roundoff is always going on, so the answers are only 2 decimal place approximations. Your calculator probably allows as much as 8 places.

Problem Set #3

Complete each triangle :

1.

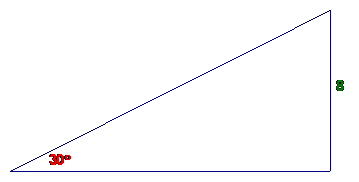
2.

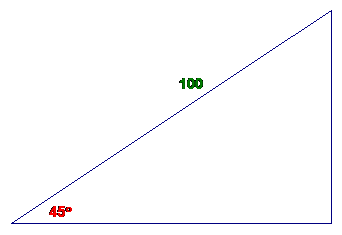
3.

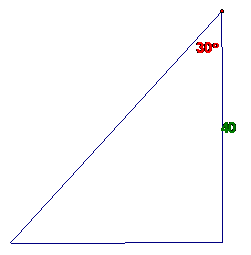
4. A 12” wide board which is 8’ long is lying is attached so that it is at a 30 degree angle to the ground. The sun is directly overhead. What will be the area of the shadow made by the board on the ground?

5. A truck is driving on a highway in the Rocky Mountains west of Denver. The driver begins to go downhill and sees a sign saying “Caution: 5% slope next 10 miles”. Draw a sketch which accurately reflects this information.

Follow this link for solutions to Problem Set #3

1.4 Degrees and Radians

Depending on the books you use or courses you take, angles may be specified in either degrees or radians. You need to be competent in both. This is easy.

First we assume you are familiar with degrees and know there are 360 degrees in a complete circle.

Secondly we point out that there are also 2π radians in a circle, or about 6.28 radians because π is approximately 3.14

Thus we have the critical conversion formula

360° = 2π radians

or

180° = π radians

This last formula is really all you need to remember!! Just multiply or divide accordingly and you can make any conversion.

For example:

60° = π/3 radians (just divide by 3)

90° = π/2 radians

150° = (5/6) π radians

with this kind of simple algebra, we can rebuild our trig table from earlier:

θ (deg)	θ (rad)	sin(θ)	cos(θ)
0°	0	0	1
30°	π/6
45°	π/4
60°	π/3
90°	π/2	1	0

and comment that you really should memorize both ways, degrees and radians.

Problem : What about the other direction?

What does 2 radians convert to in degrees? We have from above that

180° = π radians

Dividing both sides by π we have what 1 radian is

180°/ π = 1 radian

Multiplying both sides by 2 gives us

360/ π° = 2 radians

Now if you get out your calculator and divide 360 by 3.14 you find we have about

114.59° ≈ 2 radians

to finish the problem. Note we carried the units all the way along for clarity.

Now while we are at it, we can divide by 2 and find the useful fact that

57.29° ≈ 1 radian

Problem Set #4

1. Convert each degree measure into radians. If convenient, leave your answer in terms of π.

a) 30°

b) 55°

c) 720°

d) 270°

e) 225°

2. Convert each radian measure into degrees

a) 5 π/6

b) 6π

c) π/10

d) 9π/2

e) 1 radian

3. list 5 different values of θ for which each equation is true:

a) cos(θ) = 0

b) sin(θ) = -1

c) tan(θ) = 1

Follow this link for solutions to Problem Set #4

1.5 Trig Identities

The Pythagorean Theorem says that, for our original right triangle,

Hyp² = Adj² + Opp²

Dividing both sides by Hyp² we then easily have

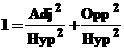
and if we remember SOH CAH TOA, this is the same as

1 = sin²(θ) + cos²(θ) (trig identity #1)

this is a very useful identity and should be memorized. It is really nothing more than the Pythagorean Theorem applied to sine and cosine.

From SOH CAH TOA we have that

tan(θ = Opp/Adj

but sin(θ) = Opp/Hyp and cos(θ)= Adj/Hyp so

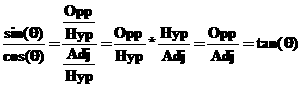
so tan(θ) = sin(θ)/cos(θ)) (trig identity #2 )

If we divide both sides of trig identity #1 by cos²(θ) then we have

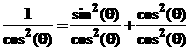
or, since 1/cos is defined as secant,

sec²(θ) = tan²(θ) + 1 (trig identity #3)

This identity appears often in calculus courses.

Other identities:

sin(2θ) = 2 sin(θ) sin(θ) (identity #4)

(identity #5)

(identity #6)

which are used in Calculus II and Differential Equations, among other places.

Problem Set #5

Use trig identities to simplify each expression as much as possible

1. sin⁴θ – cos⁴ θ

2. 1 – cos² θ

3. cos⁸ θ - sin⁸ θ

4. cos² θ - cos⁴ θ

Solve the following equation for x

2sin²x – cosx – 1 = 0

Follow this link for solutions to Problem Set #5

Part 2. Oscillating Functions

The other use of trig functions is for oscillations. These occur in vibrations in physics and mechanical engineering as well as electrical circuits.

2.1 Basics of Sine and Cosine

For starters we begin with a circle of radius one and a radius from the origin to a point (x,y) on it.

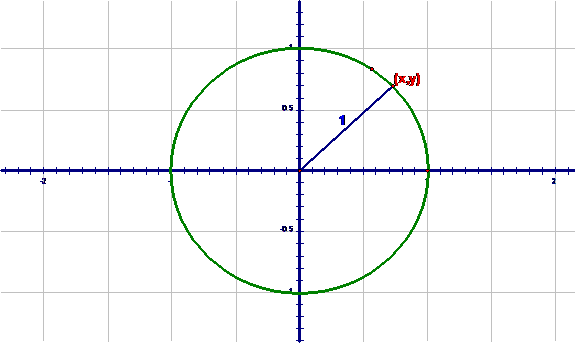
Now if we drop a perpendicular to the x axis then we have a familiar looking right triangle:

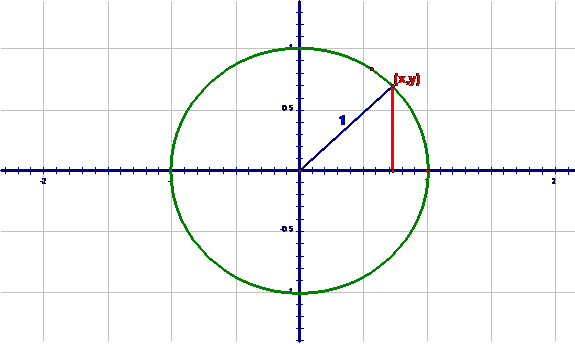
and if θ is the angle between the x-axis and the radius then the horizontal and vertical sides, respectively, have lengths of cos(θ) and sin(θ). Remembering how Cartesian coordinates are plotted, this means that

x = cos(θ) and y=sin(θ)

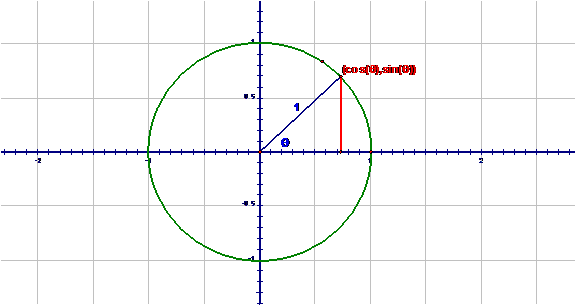
Now at this point, this is nothing more than we did earlier, just superimposed on the x-y coordinate system. We even have a table of the coordinates of x and y for 5 different values of θ.

What becomes new is when θ exceeds 90° and we move in to the other quadrants instead of remaining in the first quadrant.

We need to take a second and review the signs (+, -) of points in other quadrants:

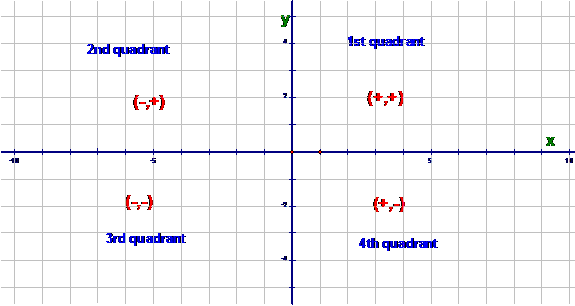
If, for θ > 90°, we define x as cos(θ) and y as sin(θ) then the functions take on both positive and negative values.

The graphs of Cosine and Sine, plotted versus the angle θ, look like:

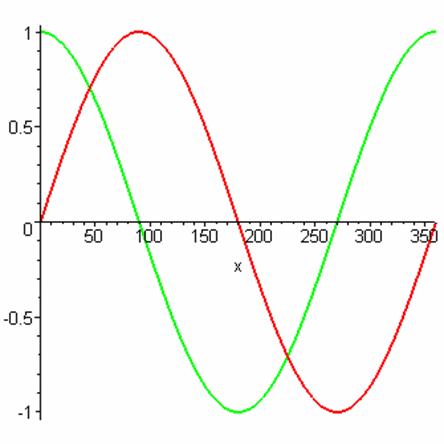
where Cosine is in green and Sin is in red. The reader should compare the values on the graphs above, for the first 90 degrees, with those obtained earlier and put into the table. This graph is fundamental to an understanding and application of Sin and Cosine as oscillating functions . We refer to it in the remainder of this document as Graph I

θ	sin(θ)	cos(θ)
0°	0	1
30°
45°
60°
90°	1	0

The only trouble with this is that the values in the table are in fraction form. If they are converted to decimals then it might be easier to relate to the graph. This is done below:

θ	sin(θ)	cos(θ)
0°	0.00	1.00
30°	.500	.866
45°	.707	.707
60°	.866	.500
90°	1.00	0.00

Now the first thing we need to point out is that in Graph I, the green and red graphs are really the same curve. Please note that if you shift the Green curve (Cosine) to the right by 90°, then you have the Red (Sine) curve. From an algebraic point of view this is the same as saying

Sin( θ + 90°) = Cos(θ)

This is often referred to by saying that the two curves are out of phase (by 90 degrees) relative to one another, or that one has a phase shift of 90 degrees.

A different way of looking at it is to say that

Cos(( θ -90°) = Sin(θ)

because you can shift the Cosine curve 90 degrees to the left (hence the – sign) and you then have the Sine curve. This should look familiar. If you go back to the beginning of this material to the section on Complimentary Angles, you will find the same identity.

2.2 Amplitude, Frequency and Phase Shift

Amplitude

Suppose instead we looked at the curve y = 3sin(θ) and compare it to y = sin(θ) which we have already graphed. The simplest route is to realize that for every θ value on the horizontal axis, the y value on the vertical axis is 3 times as high. If we superimpose both graphs on the same document, they are easy to compare:

Recall that originally we developed these graphs from a unit circle. The graph y = 3sin(θ) comes from a circle of radius 3.

So putting the two results together, phase and amplitude, we have that for the curve y = A sin (θ + c) we have that the parameter A changes the amplitude (height) from 1 to A while the value of c shifts the graph right by c units (if c is positive)

Frequency

Let’s now consider y = sin(θ) vs y = sin(4θ). What effect does the 4 have? From a numerical point of view, with the aid of a calculator, a comparative table can quickly be built

θ	sin(θ)	4θ	sin(4θ)
0°	0	0°	0
15°	.259	60°	.866
30°	.500	120°	.866
45°	.707	180°	0
60°	.866	240°	-.866
75°	.966	300°	-.866
90°	1	360°	0

This means that y = sin(4θ) has gone through an entire complete oscillation in 90 degrees while sin(θ) has only gone through a quarter of that! So the graphs look like:

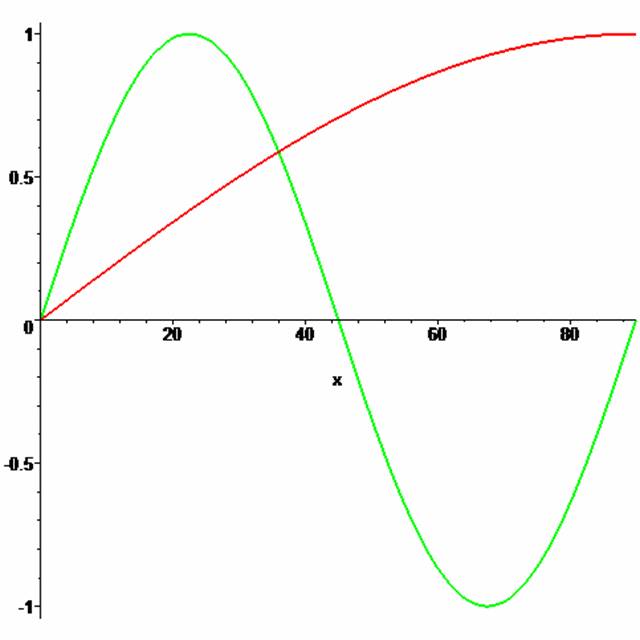
and, if we extend the graphs further for θ from 0° to 360° we get two graph appearing as:

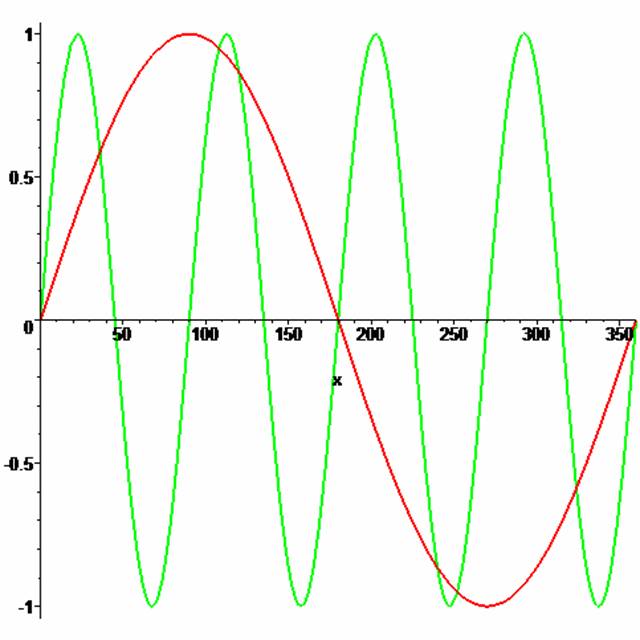
more importantly they show us that the green graph, sin(4θ) has gone through 4 complete cycles in the time that sin(θ) has only gone through one single cycle! It is oscillating 4 times as fast!

In general, if we compare the graphs of y = sin(kθ) and y = sin(θ) the first one oscillates k times as fast as the second one.

Putting all of this together: For a graph of y = A sin(kθ + c) vs y = sin(θ), the three parameters A, k and c have the effects:

A amplitude (how high and low the graph oscillates)

k frequency (how quickly it oscillates)

c phase shift (how it is shifted to the right if c >0; left if c<0)

For example, y = 40sin(10θ + 45) in degrees, may be thought of as having an amplitude of 40 units, as well as 10 oscillations every 360°, and a phase shift of 45° to the right.

As a second example, in a problem where radians are assumed to be the measure of angles, y =250sin( 20θ –π/4). This can be interpreted as an amplitude of 25 units, there are 20 oscillations every 2π units of time, and there is a shift of π/4 to the left.

Comment: in the last example, if there are 20 oscillations every 2π units of time then there are 20/2π oscillations every unit of time. This is often referred to as the frequency of the object with the units being cycles per second. Since 20/2 π is approximately 3.18, this means the curve is making 3.18 oscillations every second. In music, an A note is 440 cycles per second ( see http://en.wikipedia.org/wiki/Music_theory) The amplitude, A, then determines how loud the note is heard.