
Author: Brigitte Servatius, Tomaž Pisanski, and Doris Schattschneider.
Reference: Mathematics Magazine 79 no. 3, 167--180, 2006.
Abstract:

Our point of departure is a problem of M. C. Escher, solved using methods of contemporary combinatorics, in particular, Burnside's lemma. Escher originally determined (by laborously examining multitudes of sketches) how many different patterns would result by repeatedly translating a 2x2 square having its four unit squares filled with copies of an asymmetric motif in any of four aspects. In this note we simplify the problem from two dimensions to one dimension but at the same time we generalize it from the case in which a 2x2 block stamps out a repeating planar pattern to the case in which a 1xn block stamps out a repeating strip pattern. Selected Figures:

A 1x3 Strip Pattern.
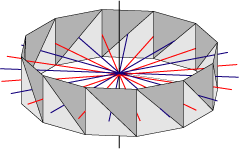
Rotational symmetry axes of a 12-ring.
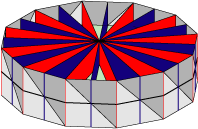
Reflection mirrors of a 12-ring.
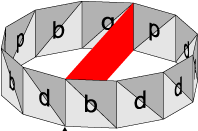
A 1x12 strip template.