Symmetry pairings of the sphere

Title: The 24 symmetry pairings of self--dual maps on the sphere (download pdf) (abstract)

Authors: Brigitte Servatius and Herman Servatius

Reference: Discrete Mathematics 140 (1995) 167-183

Selected Figures:

Example of pairing $[3,4]^+ > [3,3]^+$
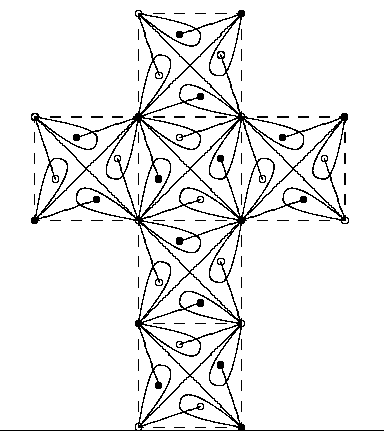
Example of pairing $[3,4] > [3,3]$

These graphs are drawn on unfolded cubes. The best way to view them is to print them out, color the edges joining solid vertices red, edges joining hollow vertices blue, cut them out, and fold them into cubes. An entire set of 24 appears in the paper, as well as instructions on how to make your own self-dual maps and polyhedra.

Abstract: Given a self--dual map on the sphere, the collection of its self--dual permutations generates a transformation group in which the map automorphism group appears as a subgroup of index two. A careful examination of this pairing yields direct constructions of self--dual maps and provides a classification of self--dual maps. Examples from each of the symmetry classes are given.