Author: Brigitte Servatius and Herman Servatius

Reference: Discrete Math. \vol{134}, 139--150, 1994.

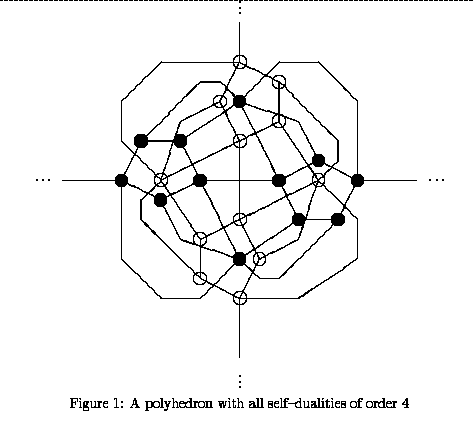
Selected Figures:

• Some Self-Dual Maps
  
  
• The smallest 3-connected self-dual map of rank 4
  
  

Abstract: A map is a planar drawing of a graph on the sphere or plane. The dual map is obtained by drawing one vertex in the interior of each reagon determined by the map, and connecting the vertices of regions with a common boundary by a single edge crossing the boundary edge once, transeversly, A map is self-dual if the map and dual map are isomorphic. We show how to recursively construct all self--dual maps on the sphere together with their self--dualities, and classify them according to their edge--permutations.

Other articles on Symmetry and Duality

Go to Discrete Mathematics