Authors: Brigitte Servatius and Herman Servatius
Reference: Graph Theory Notes of New York, 23, 25-28, 1992.
Selected Figures:


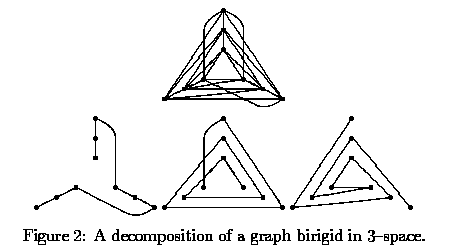
Abstract: A set $F$ of edges is said to be {\em isostatic} if it is both independent and rigid, and if $E=F$, then we say the graph $G=(V,E)$ is isostatic. Lovasz and Yemini observed that Laman's condition for a graph $G$ to be isostatic is related to a theorem by Nash--Williams: $E(G)$ is isostatic if and only if adding any edge to $G$ yields the edge disjoint union of two spanning trees. Equivalently, $E(G)$ is independent in $M(2,n)$, if, after adding any edge to $G$, the resulting graph can be decomposed into two spanning forests. Recski proved that in the above statements, ''adding any edge to $G$'' may be replaced ''by doubling any edge of $G$'', and it has been shown in by Crapo that
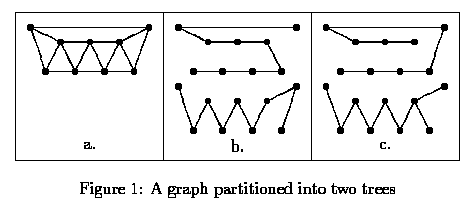
A graph $G$ on $n$ vertices is a cycle in $M(2,n)$ if and only if it is the edge disjoint union of two trees no two of whose subtrees have the same span.