Graduate Presentations
Session 1 - Salisbury Labs 104
9:00-9:15 Cartesian Products of Triangles as Unit Distance Graphs
Ryan Sternberg and Gregory Case,
Worcester Polytechnic Institute
The Cartesian product of n triangles is a unit distance graph of
diameter n.
It is difficult to produce a drawing of such a graph in the plane such that
adjacent vertices are unit distance apart. The difficulty arises because the
number of vertices increases exponentially while the diameter increases
linearly in n. Moreover, the graph realized as a mechanism has n-1 degrees
of freedom. We analyzed the motion of these graphs and examined their graph
theoretic and combinatorial properties.
9:20-9:35
Local Isomorphisms Among Low Dimensional Lie Groups
John Gonzalez, Northeastern University
During the early twentieth century Killing and Cartan gave a complete
classification of all simple Lie algebras over the complex numbers. A result
of the classification is the existence of isomorphisms among certain low
dimensional Lie algebras, which implies the existence of local isomorphisms
among certain classical matrix groups. The construction of these local
isomorphisms is not apparent from the classification. Only a general
existence theorem is proven. In this talk we will describe a general method
for constructing these local isomorphisms and apply this method to outline
the isomomorphism between SL(4,C) and SO(6,C).
9:40-9:55 The Dynamic Exchange of Solutes during Hemodialysis
Edward Boamah, University of Vermont
The focus of this research is to develop testable mathematical models for
the dynamic exchange of solutes (e.g., bicarbonate) in high flux-dialyzers.
The blood and dialyzate flow rates and hemodialysis duration are taken into
account. The model was used to compute the minute by minute bicarbonate,
partial pressure of carbon dioxide and hydrogen ion concentrations. The
models compare very well with hemodialysis clinical data.
Session 2 - Salisbury Labs 105
9:00-9:15
Nonlinear Evolution of Small Disturbances from Boundary Conditions
in Flat Inclined Channel Flow
Richard Spindler, University of Vermont
We determine the asymptotic behaviour of small disturbances from boundary
conditions in a flat inclined channel.
These small disturbances develop into
the quasi-steady pattern called roll waves, first discussed by Dressler in
1949. Roll waves exist if F, the Froude Number, of the flow exceeds 2, which
consist of a periodic pattern of bores, or discontinuities. After confirming
the instability condition for F>2 for the linearized equations
in the boundary value case, we study the non-linear boundary value problem
for the weakly unstable region of F slightly larger than 2. We apply
multiple scales over long distances to determine the evolution of the
solution over space. The resulting evolution equations are found by applying
Fredholm Alternative Theorem. It is found that the solution is dominated by
the evolution of the solution along one characteristic.
9:20-9:35
The Vese-Chan Algorithms Revisited: A Level Set Method for Image
Segmentation and Fracture
Casey Richardson, Worcester Polytechnic Institute
Variational models for image segmentation and fracture are similar
mathematically, but notoriously difficult to solve and to approximate
numerically. These difficulties are illustrated by the Mumford-Shah problem,
where the main difficultly is the presence of the unknown free surface and
its numerical treatment. There are numerical methods for solving this
problem, but these tend to find only local minimizers. Recently, Luminita
Vese and Tony Chan introduced numerical schemes based on level set
descriptions of the free surfaces, the level set methods of Osher and
Sethian, and Dirichlet-Neumann maps on overlapping domains. \ These schemes
however have two drawbacks: First, although it is known that only triple
junctions can occur in local minimizers, the Vese-Chan algorithms generally
result in quadruple junctions. The second, more serious, limitation of these
methods is that they are incapable of finding crack tips, which is critical
in models for fracture. In this talk, we will introduce several
modifications of these schemes to get around both of these limitations.
Numerical experiments will be presented.
9:40-9:55 Newton-Krylov Methods for Expensive Functions
Rebecca Wasyk, Worcester Polytechnic Institute
Newton-Krylov methods have proven useful for solving large scale nonlinear
systems. An advantage of these iterative methods is that they do not require
storage of the system Jacobian, but only require knowledge of how the
Jacobian acts on a vector. A difference quotient evaluated at each linear
iteration is often used to approximate this action without slowing the
convergence rate of the method. For systems with expensive nonlinear
function evaluations, however, the requirement of a function evaluation for
each linear iteration can result in a very costly computation. This work
focuses on theoretical and numerical results that determine the convergence
rates and time savings possible when implementing an algorithm with an
approximation to the system function in the difference quotient.
Session 3 - Higgins Labs 154
9:00-9:15
The Escape Trichotomy for Singularly Perturbed Complex Polynomials
Daniel M. Look, Boston University
We describe certain Julia sets of functions that are singular perturbations
of complex polynomials. We show that for this particular family of maps we
have an "escape trichotomy" that is
analogous to the well-known fundamental dichotomy for complex polynomials.
In particular, we give criteria for the Julia set to be a Cantor set, a
Cantor set of circles, or a Sierpinski curve.
9:20-9:35
Proximity in Group Inverses of M-Matrices and Inverses of Diagonally
Dominant M-Matrices
Minerva R. Catral, University of Connecticut
The connection between the mean first passage matrix of a finite homogeneous
ergodic Markov chain and the group inverse of an associated M-matrix was
given by C. Meyer in a famous 1975 paper. In this talk we connect,
generalize, and broaden properties of matrices related to: (i) the
triangular inequality for mean first passage times in finite homogeneous
ergodic Markov chains, (ii) the triangle inequality for proximities in
Laplacian matrices of undirected weighted graphs, and (iii) the Metzler
property of the column entrywise diagonal dominance of inverses of
diagonally dominant M-matrices. This is joint work with Michael Neumann and
Jianhong Xu.
9:40 - 9:55 Regular Binary Hermitian Forms
Anna Rokicki, Wesleyan University
Let h be a positive definite binary integer-valued Hermitian form over an
imaginary quadratic field. A Hermitian form h is called regular if h
represents all integers that are represented by the genus of h. It is shown
that for a given field there exist only finitely many inequivalent Hermitian
forms. It is also shown that there are only twelve imaginary quadratic
fields which support those h that are regular and normal. For those fields I
will give a compile list of 55 inequivalent binary Hermitian forms which
contains representatives from all classes of the decomposable regular
integral Hermitian forms.
Session 4 - Higgins Labs 218
9:00-9:15
Period Two Solutions of a Third Order Rational Difference Equation
Eugene Quinn, University of Rhode Island
We investigate the character of solutions of a third-order rational
difference equation which converge to a periodic solution with period two.
In particular, we discuss the monotonicity of the subsequences of even and
odd terms in the solution sequence.
9:20 - 9:35
On the Trichotomy Character of 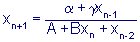 for n=0,1,...
for n=0,1,...
Esha Chatterjee, University of Rhode Island
We investigate global character of solutions of the nonlinear third order
rational difference equation in the title, where the parameters B and the
initial conditions and are non-negative real numbers. In particular, we
investigate the global stability, the periodic character, and the
boundedness nature of all solutions. We show that the solutions of this
equation exhibit a trichotomy character which depends upon whether is less
than A, equal to A, or greater than A.
9:40 - 9:55
On the Periodicity Character of
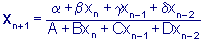 for n=0,1,...
for n=0,1,...
Yevgeniy Kostrov, University of Rhode Island
We investigate the existence of prime period-two solutions of the nonlinear
third order rational difference equation (1), where the parameters and the
initial conditions and are non-negative real numbers. We show that if
Equation (1) has a prime period-two solution, then it either has essentially
a prime period-two solution, or else has infinitely many prime period-two
solutions.
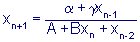 for n=0,1,...
for n=0,1,...
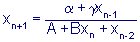 for n=0,1,...
for n=0,1,...
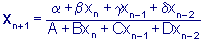 for n=0,1,...
for n=0,1,...