Lab1: Vector Fields and Line Integrals

Goal:
This lab will help you to explore and understand some key ideas in the study of line integrals. You will use Maple VI

• to visualize vector fields e.g. the gravitational force field, the electric field;
• to compute line integrals, e.g. the work to move a particle through an electric field;
• to see the difference between conservative and nonconservative vector fields.

In Maple, one has access to many different libraries of specialized functions. Among these are statistical tools in stat, graphical tools in plots, and linear algebra tools in linalg. We will use the latter two toolboxes.
To use the toolboxes, you must load them with the command
$>$ with(plots): with(linalg):

Background:
Consider a curve $C$ described by ${\bf r}(t)$ for $t$ going from $a$ to $b$, so that ${\bf r}(a)$ is the starting point of the curve and ${\bf r}(b)$ the ending point.
The line integral of $f(x,y,z)$ along the curve $C$ with respect to arclength $s$ is:

$$\int_C f(x,y,z) \, ds = \int_a^b f({\bf r}(t)) \vert{\bf r}'(t)\vert \, dt.$$

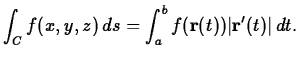
One important application of the line integral is in computing work.
The work $W$ to move a particle along a curve $C$ through a vector force field F is given by the line integral

$$W = \int_C {\bf F}\cdot {\bf T} \, ds = \int_C {\bf F}\cdot d{\bf r}.$$

To actually compute the work, we compute the integral

$$\int_C {\bf F}\cdot d{\bf r} = \int_a^b {\bf F}({\bf r}(t))\cdot{\bf r}'(t) \, dt.$$

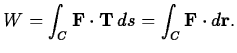
If, for the same starting and ending points, no matter what path $C$ you use in between, you always use the same amount of work to get from the starting point to the ending point, the vector field ${\bf F}$ is called conservative. Otherwise, it is called nonconservative.

Maple Implementation:
We can get Maple to do a lot of work, both computationally and graphically, for us. Specifically, we will go through the steps to

• set up the vector field,
• plot it,
• set up the curve $C$ (by defining ${\bf r}(t)$),
• plot the curve,
• have Maple compute ${\bf F}({\bf r}(t))\cdot {\bf r}'(t)$,
• integrate that expression to get the total work, $W$.

The following example will find the work to move through the force field ${\bf F}(x,y,z)=(x^2,y+z,z^2).$
Load the plots and linalg toolboxes.
$>$ with(plots): with(linalg):
Set up the vector field and plot it.
$>$ F:=[x^ 2,y+z,z^ 2];
$>$ fieldplot3d(F,x=-1..1,y=-2..2,z=-3..3,axes=normal);
For the fieldplot3d command, you must give the plotting function a range in space to plot over. Also, to have the coordinate axes appear, the axes option was included. You should use help to see more about fieldplot3d and the accompanying options.
Use the mouse button to rotate your plot.

Now, define a curve $C_1$ with the parametrization ${\bf r}(t)=(x(t),y(t),z(t))$ as follows:
$>$ x:=2*cos(t); y:=2*sin(t); z:=3*t;
$>$ r:=[x,y,z];
and then plot ${\bf r}$ to see what it looks like.
$>$ spacecurve(r, t=0..4*Pi, axes=normal);
This curve is a helix. We need a tangent vector to it for our integral, so we issue the command
$>$ dr:=diff(r,t);
and finally set up the integral by doing the dot product of ${\bf F}({\bf r}(t))$ with the tangent vector
$>$ integrand:=innerprod(F,dr);
To get the total work, we just perform a definite integral from 0 to 4$\pi$.
$>$ W:=int(integrand,t=0..4*Pi);
which should come out to be $576\pi^3$. This is the total work to move against the given force field along the helix for two revolutions.

Note on Cleanup:
We assigned specific expressions to x,y and z. We want to deassign those before using the commands again, so issue the command.
$>$ x:='x'; y:='y'; z:='z';

Discussion:
The starting point of the curve above was r(0) = (2,0,0), and the final point was r($4\pi$) = (2,0,12$\pi$). You can check this by typing
$>$ t:=0; r; t:=4*Pi; r; t:='t';
Once again, it is very important that you set t back to a variable. The total work to go from (2,0,0) to (2,0,12$\pi$) along the curve given was 576$\pi^3$.
Let's try another path between the two points.
Consider the curve $C_2$ with parametrization ${\bf r}(t)=(2\cos(t),t(t-4\pi),3t)$ for $0 \leq t \leq 4\pi$. Does this curve connect the two points? Check this.
Using the same set of commands we just entered, show that the total work along this curve comes out to $608\pi^3$. (Make sure you change the limits of integration so that you get the integral to go from $(2,0,0)$ to $(2,0,12\pi)$.) It takes more work to go along this path than it does along the helix. Thus, the field $F(x,y,z)=(x^2,y+z,z^2)$ is certainly a non-conservative force field; otherwise we would always have W=576$\pi^3$ when we go from $(2,0,0)$ to $(2,0,12\pi)$.

Now, a little logic. Had we gotten $576\pi^3$ again, this would not necessarily mean we had a conservative field; it would just suggest the possibility of it. There is no such thing as ``proof by example'' but there is ``disproof by counterexample,'' which is what we just did.

As one last demonstration of why this force field above is nonconservative, try computing the work to move along the curve $C_3$ as described by

$${\bf r}(t)=(t^2/18\pi^2, t^2-36\pi^2, 6\pi+t)$$   for$$-6\pi \leq t \leq 6\pi.$$

What does this curve look like? Does it have the right starting and ending points? Show that the work to move through the force field along this path is $864\pi^3$.

Exercise ONE
Consider the force field

$${\bf F}(x,y,z) = -x/(x^2+y^2+z^2)^{3/2} {\bf i} - y/(x^2+y^2+z^2)^{3/2} {\bf j} -z/(x^2+y^2+z^2)^{3/2} {\bf k}.$$

Thus, ${\bf F} = {-{\bf x/\vert{\bf x}\vert} \over \vert{\bf x}\vert^2} = -{\bf x}/\vert{\bf x}\vert^3.$ This vector field, save for a constant multiplier, is the same as the Newton's gravitational force field, and the electrostatic field.

1. Plot the vector field F. Describe the features of the plot you see. Rotate the plot to get different vantage points.
2. Compute the work to move from (2,0,0) to $(2,0,12\pi)$ (i) along the curve $C_1$ and (ii) along the line segment connecting the two points. What conjecture can you make based on the computations you made?

A Tool for distinguishing Conservative and Nonconservative Force Fields - CURL
At this point, we know if we find the work to go between two points along two different paths and get different results, then we have a nonconservative force field. If we get the same amount of work, we only know we might have a conservative force field. Some other path might require a different amount of work; we can't say for sure. So we need some definite way to tell, and computing lots of line integrals won't do it. One tool (there are several) is the curl operator. It is easy to use so we introduce it here.

The curl operator applies only to vector fields. It gives another vector field as the result. We will use the result below which we will prove later on in the course.

• if the curl of a vector field is 0, then the field is conservative;
• if the curl is other than 0, the field is nonconservative.

Here 0 means the zero vector.

To compute a curl by hand would require partial derivatives, but we can get Maple to do it for us instead. If F is a vector field set up as earlier, then the command
$>$ curl(F, [x,y,z]);
gives the curl of F. You must first ensure that x, y, z are indeed variables, so make sure you deassign them.
As an example of the curl,
$>$ F:=[x^ 2,x*y*z,y^ 2];
$>$ curl(F, [x,y,z]);
yields the answer
[2*y-x*y, 0, y*z]
which shows this force field is non-conservative.
If we had used
$>$ F:=[2*x*y*z, x^ 2*z + 2*y, x^ 2*y];
$>$ curl(F, [x,y,z]);
the output would be
[0,0,0];
indicating the force field was conservative.

The curl operator provides a very quick and accurate way to tell if a force field is conservative or not. Why it is called such a thing will be discussed later in the course, as well as further physical interpretations of it.

Exercise TWO
Compute the curl of each of the vector fields used earlier. What conclusions can you draw?

Exercise THREE
Consider a 2-dimensional inverse square law force field:

$${\bf F}(x,y) = -x/(x^2+y^2)^{3/2} {\bf i} - y/(x^2+y^2)^{3/2} {\bf j},$$

that we qualitatively use to describe the force on a positive charge due to the presence of a negative point charge at $(0,0)$.

1. Plot the vector field of ${\bf F}$.
2. Define a scalar field $G(x,y)$ that is equal to the magnitude of the force at the point $(x,y)$.
3. Use Maple to plot the level curves of the magnitude of this force field. Use the Maple command contourplot.
4. What should the level curves look like? Is this what you see? Discuss.
5. Give the definition of ${\bf H(x,y)}$ which we can use to describe the force on a positive charge at $(x,y)$ due to the presence of a negative point charge at $(0,0)$, a positive one $(1,0)$ and another negative one at $(0.5,0.5)$.