The area of a triangle was presented based on the following calculation:

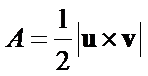
Where u and v were two vectors emanating from a common point. A triangle has 3 points (P_i, P_j, P_k). By default, u could be (P_j - P_i) and v could be (P_k - P_i). This formulation is valid in 3D as well as 2D. Albeit, in 2D it is much faster.

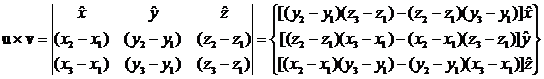
The magnitude of this 3D vector is twice the area of the triangle, or it is the area of the parallelogram swept by the cross product. Unfortunately, the magnitude requires that one square the individual directional components, sum them, and take the square root. In a planar situation, only the z direction is non-zero, hence the solution does not require squares and square roots.

Assuming a loop L for all the elements, with indices list

in(local node number, element number)

for L = 1:NE;

AREA = 0.0;

for i = 1:3;

j = in(mod(i,3)+1, L);

k = in(mod(i+1,3)+1, L);

dy(i) = y(j) - y(k);

dx(i) = x(j) - x(k);

AREA = AREA + x(in(i,L))*dy(i);

end;

AREA = AREA/2;

%

% % Alternately

%

% AREA = 0.0;

% for i = 1:3;

% j = in(mod(i,3)+1, L);

% k = in(mod(i+1,3)+1, L);

% dy(i) = y(j) - y(k);

% dx(i) = x(j) - x(k);

% end;

% AREA = (-dx(3)*dy(2) + dy(3)*dx(2) )/2;

%

% % And in 3D space it is very similar

%

% AREA = 0.0;

% for i = 1:3;

% j = in(mod(i,3)+1, L);

% k = in(mod(i+1,3)+1, L);

% dy(i) = y(j) - y(k);

% dx(i) = x(j) - x(k);

% dz(i) = z(j) - z(k);

% end;

% Ax = -dy(3)*dz(2) + dz(3)*dy(2);

% Ay = -dz(3)*dx(2) + dx(3)*dz(2);

% Az = -dx(3)*dy(2) + dy(3)*dx(2);

% Area = 0.5 * sqrt(Ax*Ax + Ay*Ay + Az*Az);