ES 3001 Thermodynamics
Mechanical Engineering Department
Worcester Polytechnic Institute
Lecture: First Law of Thermodynamics (Energy Conservation)
and Evaluating Properties
Energy (E) is most frequently expressed in terms of:
Kinetic Energy for a mass (m) at a velocity (V) (an Extensive Property)
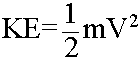
Frequently, one is interested in the change of KE from State 1 to State 2: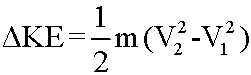
Potential Energy for a mass (m) in a gravational potential field (g) at a height z (an Extensive Property)
![]()
Frequently, one is interested in the change of PE from State 1 to State 2:
![]()
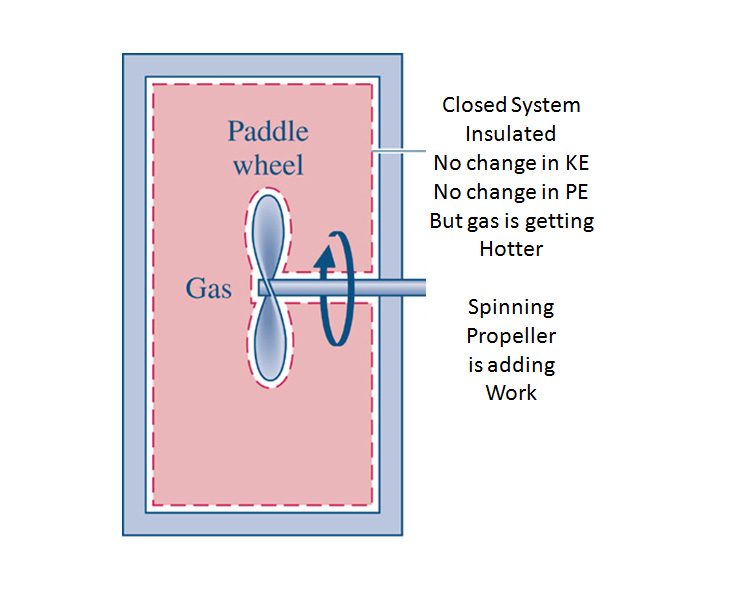
Internal Energy (U): A measure of energy at a macroscopic level due to the molecular translation, vibration, rotation (an Extensive Property). Internal Energy can also be expressed as an intensive property u=U/m (internal energy per unit mass).
Frequently, internal energy is presented in tables, such as Table A-4 for superheated water vapor.

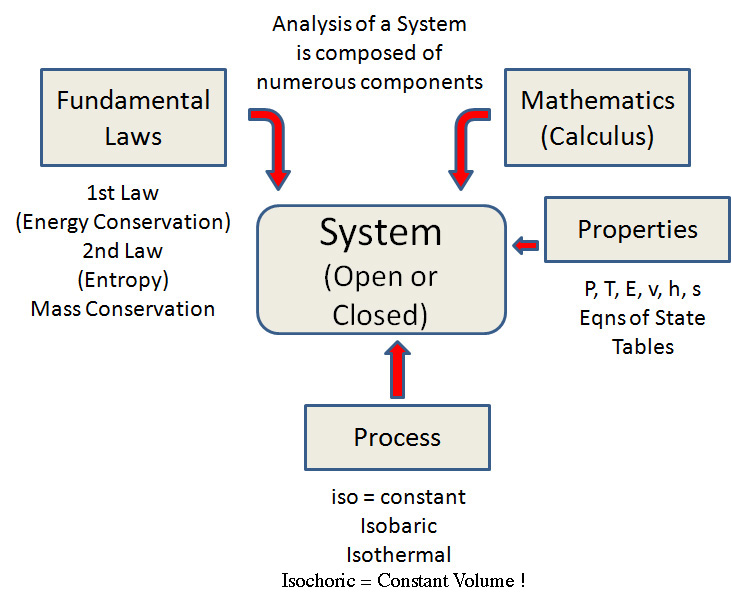
The Design and Analysis of many engineering systems requires thermodynamics (in addition to fluid mechanics, heat transfer, structural analysis, etc.)
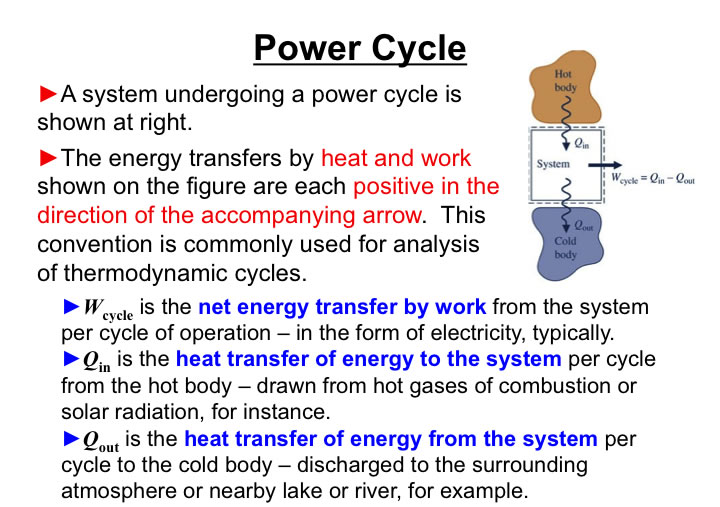
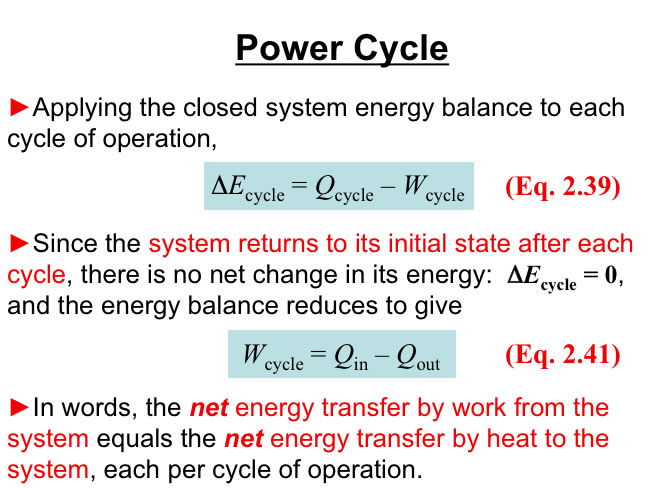
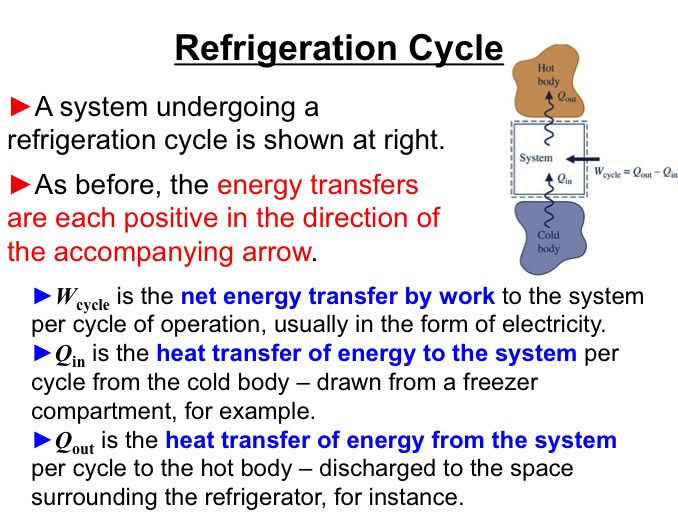
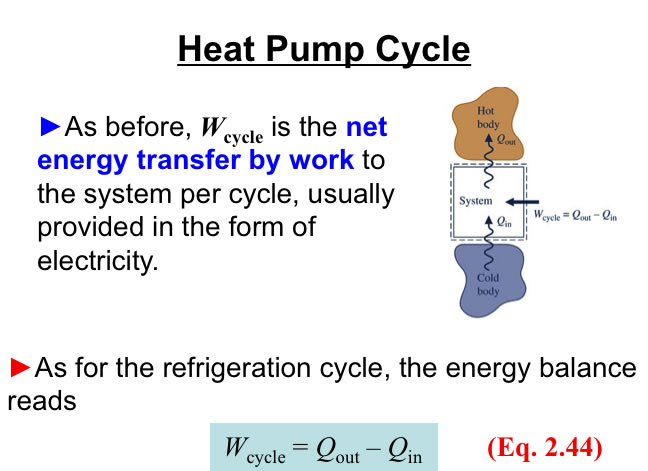
Consider a Simple Power System. Thermodynamics establishes the limits on the Maximum Power Out (Work Out) for a given Qin for a particular system of interest.

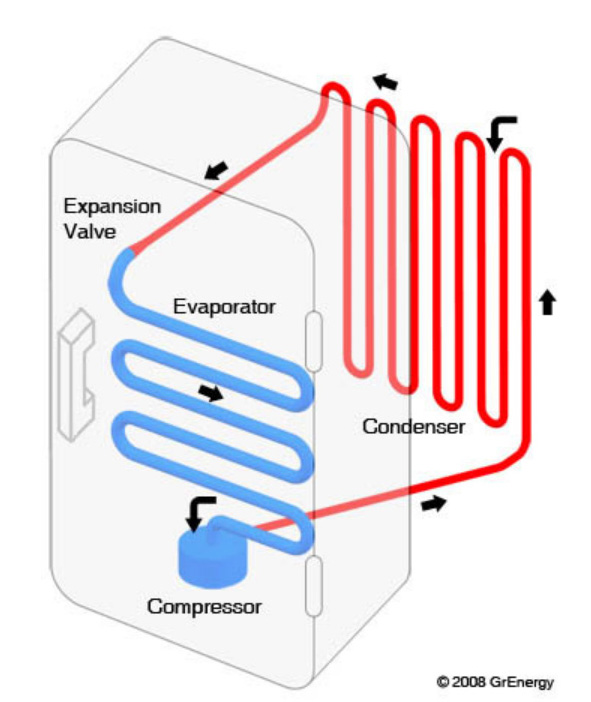
http://www.grenergy.co.uk/content/Products-HeatPumps

- The Compressor compresses the refrigerant gas and when this happens the gas gets hot as shown by the red colour in the diagram.
- This hot refrigerant gas then passes to the Condenser. The condenser is a heat exchanger which enables your heating system to extract the heat energy from the refrigerant gas. As heat is absorbed from the gas it condenses back into a liquid, still at high pressure as depicted by the orange then yellow colour.
- Having given up a lot of its heat energy, the refrigerant then passes to the Expansion Valve. The expansion valve is basically a small hole. On one side of the hole is high-pressure refrigerant liquid (yellow) and on the other side is a low-pressure area (dark blue). The dark blue side is at low pressure because the compressor is sucking the refrigerant out of that side of the system.
- As the liquid refrigerant passes through the hole to the low pressure side, it immediately boils and evaporates (dark blue), its temperature dropping rapidly to minus 33°C as described above. This very cold gas is then channelled to another heat exchanger, the Evaporator, which allows it to absorb heat from the outside air (Air Source Heat Pump – ASHP) or the ground (Ground Source Heat Pump – GSHP). As it absorbs heat, the gas warms up (light blue) after which it is channelled back to the compressor.
- The refrigerant gas is sucked up by the Compressor, and the cycle repeats.
http://www.grenergy.co.uk/content/Products-HeatPumps

http://en.wikipedia.org/wiki/File:Heat_Pipe_Mechanism.png
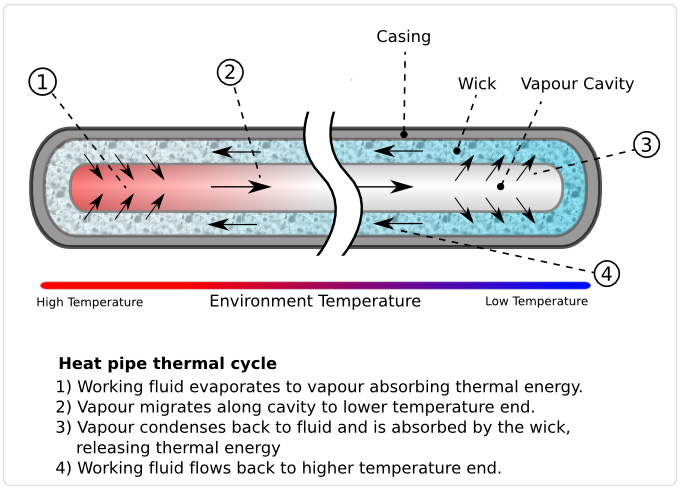
http://en.wikipedia.org/wiki/File:Heat_Pipe_Mechanism.png
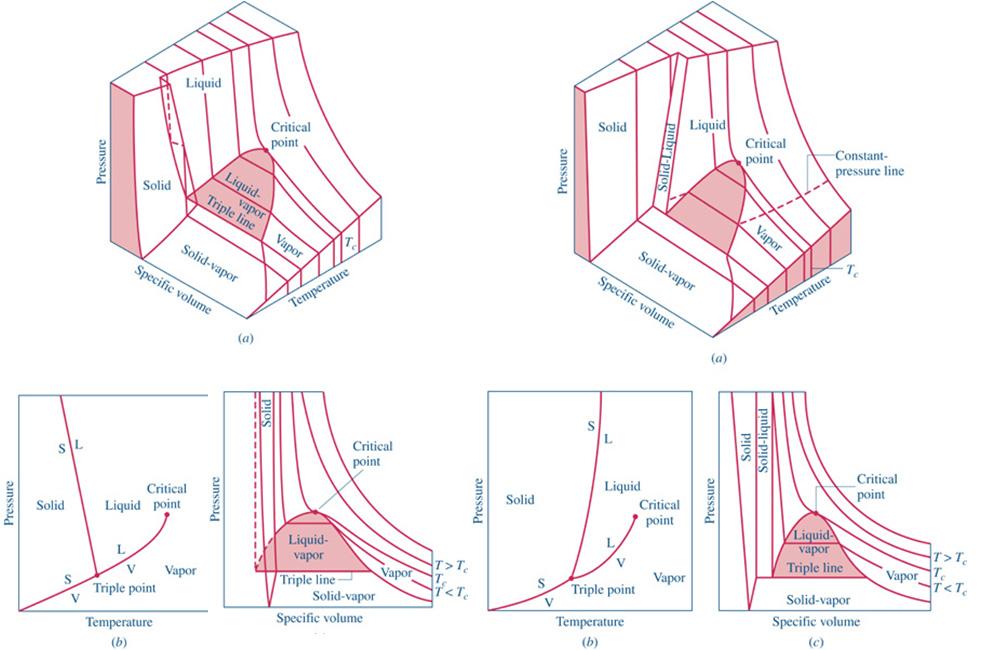
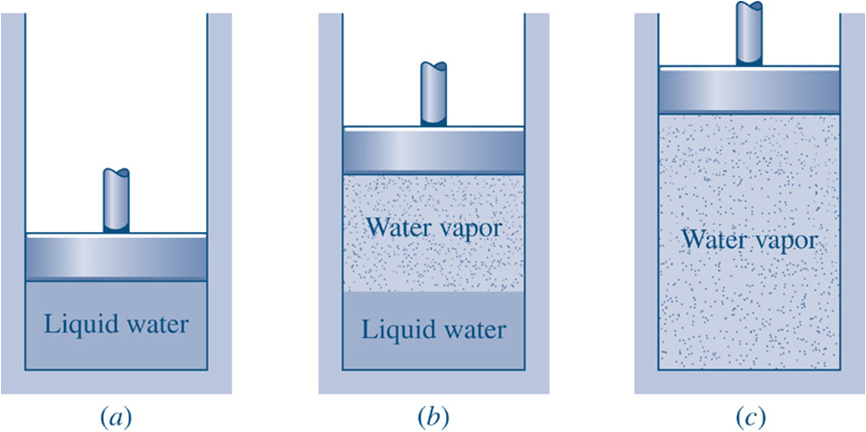

http://www.engineeringthermodynamics.org/Intro/Chapt.1_6/Chapter2a.html
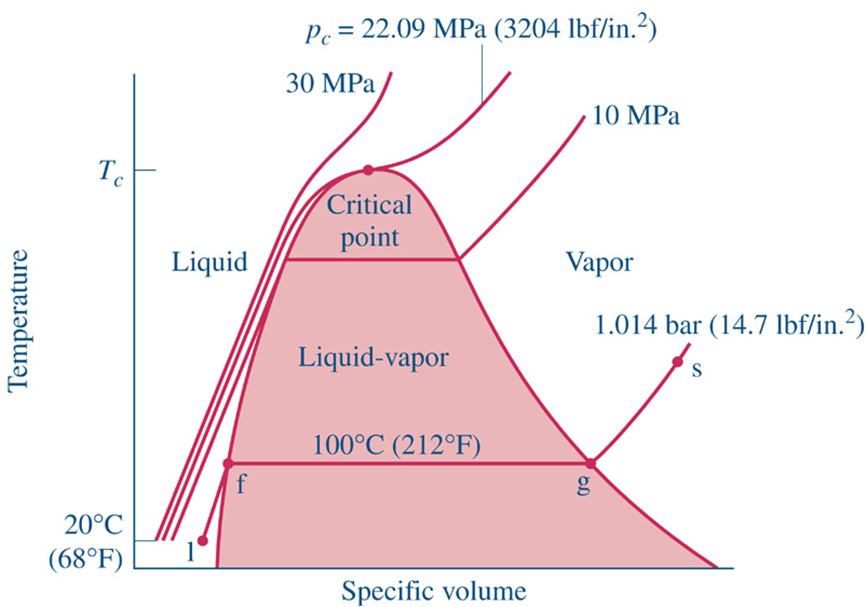
http://www.engineeringthermodynamics.org/Intro/Chapt.1_6/Chapter2a.html

http://www.engineeringthermodynamics.org/Intro/Chapt.1_6/Chapter2a.html

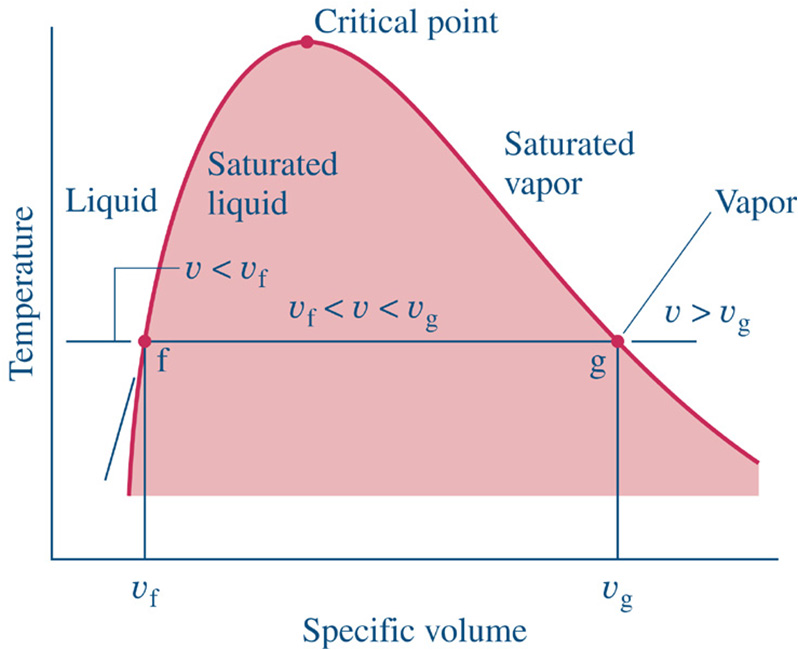
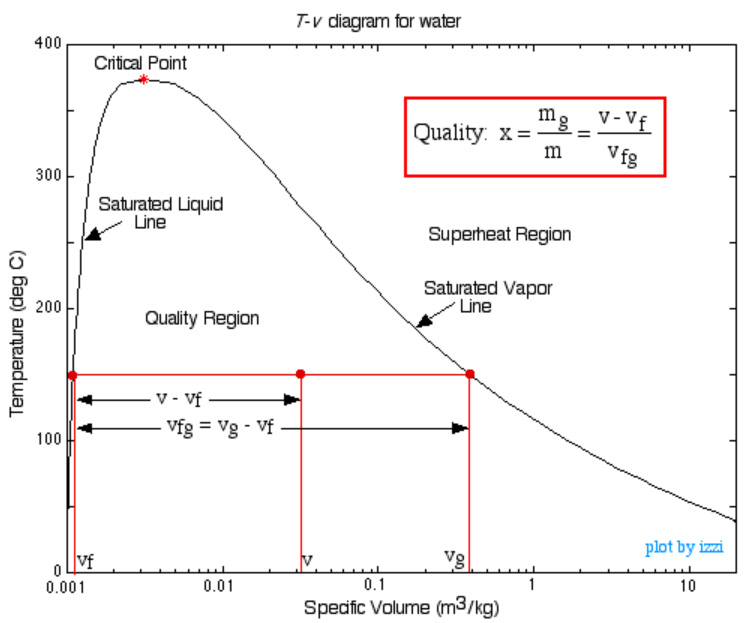
Once the substance (frequently water) is completely vapor, then Table A-4 Gives SUPERheated data

We rarely use the Compressed Liquid tables. Generally, the values are very close to those in the saturated tables at the given temperature. That is, changing the pressure of a liquid does not significantly change the state properties (other than pressure).













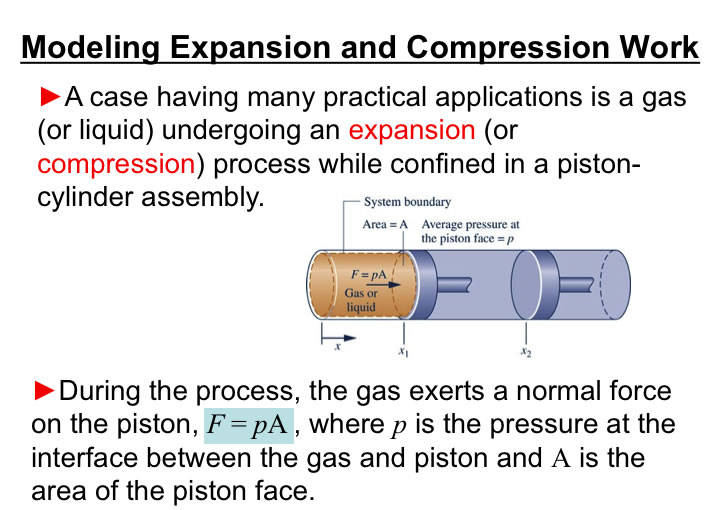



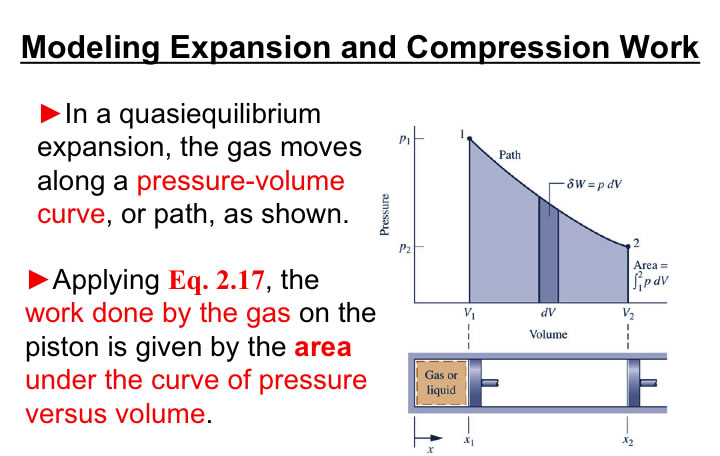


You will need to analyze the integral of PdV in order to estimate the work associated with volume expansions/compressions.
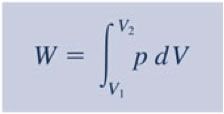
So, for polytropic situations: pVn = constant, then
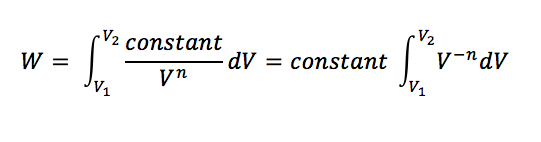
But, most gas situations will use Tables that have combined the Internal Energy (U) with the pV and a thermodynamic term (Enthalpy, H or h) is documented.
That is: H = U + pV
h = u + pv
(more on this when we reach Chapter 3)