


Next: Three plus one: modeling
Up: The rule of three
Previous: The rule of three
The modern rule of three suggests looking at mathematical concepts
from each of the numerical, algebraic, and graphical perspectives.
The purely algebraic perspective is the most common in the
introductory course:
Find the solution of the initial value problem P' = 0.015P -
0.209, P(0) = 10.
The geometric perspective is too rich to ignore:
Sketch graphs of solutions of P' = 0.015P - 0.209 for various
positive initial values. Determine the regions where the solution
curves are increasing, decreasing, concave up, and concave down.
Does P' = 0.015P - 0.209 have any constant solutions? If so,
what initial condition(s) lead to such solutions?
Sketch the direction field of P' = 0.015P - 0.209 in the first
quadrant. Identify ranges of initial conditions that lead to
qualitatively similar solution behavior.
Which of the curves shown in the figure (referring to a family of
curves, some increasing and some decreasing, of varying concavity,
including a horizontal line) might be solutions of P' = 0.015P -
0.209? Justify accepting or rejecting each curve.
Repeat the previous exercise using tables of solution values rather
than graphs.
Similarly, the numerical view is too important to postpone until late
in the course. And its exercise need not demand extensive
computation.:
The previous exercises suggest that P' = 0.015P -
0.209, P(0) = 10, will have a decreasing solution. Use one step of
Euler's method to estimate the time required for the solution to reach
P= 0.
Use Euler's method with 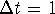 to construct a table of
values of the solution of P' = 0.015P - 0.209, P(0) = 10 for
to construct a table of
values of the solution of P' = 0.015P - 0.209, P(0) = 10 for 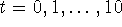 . Include in the table the values of
. Include in the table the values of 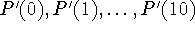 . Is the behavior you see in that table consistent with
a direction field diagram for this equation? How could you use the
entries in that table to help you draw an accurate direction field
diagram? Are the entries in the table consistent with the exact
solution?
. Is the behavior you see in that table consistent with
a direction field diagram for this equation? How could you use the
entries in that table to help you draw an accurate direction field
diagram? Are the entries in the table consistent with the exact
solution?
Use Euler's method with 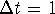 to estimate P(10).
Compare that value with the exact solution. Using available software,
repeat the computation with
to estimate P(10).
Compare that value with the exact solution. Using available software,
repeat the computation with 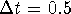 and
and 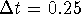 .
How does the error in the estimated value of P(10) vary with
.
How does the error in the estimated value of P(10) vary with 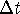 ? What return in improved accuracy does Euler's method give for the
increased work caused by halving the step size?
? What return in improved accuracy does Euler's method give for the
increased work caused by halving the step size?
The graphical and numerical perspectives are also abundant sources
of ``real'' mathematics, that material we would love to teach but for
the stupor it induces in our students.
For example, a graphical examination of solution curves can
motivate a uniqueness theorem. After students have sketched solutions of
the logistic equation 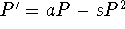 , ask whether the (stable) steady
state P = a/s is reached in finite or infinite time. The uniqueness
theorem shows that the approach is indeed asymptotic because two
solution curves can not cross.
, ask whether the (stable) steady
state P = a/s is reached in finite or infinite time. The uniqueness
theorem shows that the approach is indeed asymptotic because two
solution curves can not cross.
Analysis of the error in initial value solvers like Euler's method
requires the mean value theorem and Taylor polynomials. (Taylor
polynomials also motivate higher order Runge-Kutta methods.) When
students have explored the numerical relation between step size and
error, they are prepared to approach error analysis as a way of
understanding the potential pay back in improved accuracy from the added
computational effort of reducing step size. Central ideas of analysis
are brought into play because they help answer questions important to
the students, not just because the professor likes the concepts.
Good exercises and projects can be formulated in both the graphical
and numerical settings by letting students first discover for themselves
the basic phenomena - the possibility of an asymptote among logistic
equation solution graphs or the proportionality between numerical error
and step size in Euler's method. Then build on that motivation to
introduce the mathematical ideas that will permit students to answer the
questions their experiences have raised.



Next: Three plus one: modeling
Up: The rule of three
Previous: The rule of three
Paul W Davis
Mon Jun 23 20:58:59 EDT 1997
![]() to construct a table of
values of the solution of P' = 0.015P - 0.209, P(0) = 10 for
to construct a table of
values of the solution of P' = 0.015P - 0.209, P(0) = 10 for ![]() . Include in the table the values of
. Include in the table the values of ![]() . Is the behavior you see in that table consistent with
a direction field diagram for this equation? How could you use the
entries in that table to help you draw an accurate direction field
diagram? Are the entries in the table consistent with the exact
solution?
. Is the behavior you see in that table consistent with
a direction field diagram for this equation? How could you use the
entries in that table to help you draw an accurate direction field
diagram? Are the entries in the table consistent with the exact
solution?
![]() to estimate P(10).
Compare that value with the exact solution. Using available software,
repeat the computation with
to estimate P(10).
Compare that value with the exact solution. Using available software,
repeat the computation with ![]() and
and ![]() .
How does the error in the estimated value of P(10) vary with
.
How does the error in the estimated value of P(10) vary with ![]() ? What return in improved accuracy does Euler's method give for the
increased work caused by halving the step size?
? What return in improved accuracy does Euler's method give for the
increased work caused by halving the step size?