


Next: The rule of three
Up: Asking Good Questions about
Previous: Ask aboutnot for
We take the vocabulary of mathematics for granted and, more
fundamentally, we accept from experience the need for a well
defined vocabulary. Students frequently refuse to believe in either
the words or their necessity. Problems that explore and reinforce the
meaning of mathematical vocabulary develop mathematical literacy, a
fundamental requirement of successful analysis, problem solving, and
communication.
Like a new language, the words must be heard and spoken. We
frequently ask:
Which of the following equations are linear (or homogeneous or
...)?
Mastery of the vocabulary demands the converse, though:
Give three examples of linear (or homogeneous or ...) equations.
Give an example of a linear homogeneous equation.
Give an example of a linear equation that has the trivial solution.
Give an example of a nonlinear homogeneous equation.
Give an example of an equation that is nonhomogeneous and has the
solution y = 0.
Ask for connections among ideas upon which the vocabulary is based:
What is the amplitude of the trivial solution?
What is the amplitude of the solution of a linear homogeneous second order
equation subject to zero initial conditions?
Find the amplitude and the maximum displacement of the mass
in the spring-mass system governed by x'' + x = 0, x(0) = 1, x'(0)
= 0.
Find the period of the mass in the preceding exercise. Would
doubling the initial displacement change the period? Would it change
the amplitude?
The Laplace transform of a function is 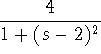 . Is it oscillatory, periodic or neither?
. Is it oscillatory, periodic or neither?
Paul W Davis
Mon Jun 23 20:58:59 EDT 1997
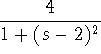 . Is it oscillatory, periodic or neither?
. Is it oscillatory, periodic or neither?