PH 1120 Term B, 1995

PH 1120 Term B, 1997

STUDY GUIDE 3

Objective 9 Resistance and Current

a) Define electric current, electric current density, drift velocity, resistance, and resistivity.

b) Given two or more simple geometric shapes of a given material, compare the resistances of the shapes.

c) Solve problems involving interrelationships among the quantities resistance, potential difference, current, current density, electric field, resistivity.

d) Define Emf and identify the internal resistance associated with an Emf.

e) Calculate the power dissipated by a resistor carrying current.

Suggested Study Procedure Study Secs. 26-1 through 26-6 and 26-9 and especially Examples 26-1, 26-2, 26-5, 26-6, 26-7, and 26-8. With this chapter, we officially leave electrostatics and begin to study situations where charge is made to move through the action of a source of emf, such as a battery. There are a number of new terms and physical relationships as indicated in the Summary at the end of Chapter 26, but the most important interrelationship is Eq. 26-11 which states that the product of the resistance of a circuit element with the current flowing through it is equal to the voltage drop across it: V = IR. Equation 26-7, a vector equation, provides the justification for the conventional direction chosen for current in a wire:
The direction of current in a wire is taken to be the direction that positive charges would move under the influence of an applied field. FOR YOUR INFORMATION AND SAFETY - READ SECTION 26-8!

Exercises and Problems Related to Objective 9

Exercises: 26-1, 26-9, 26-11, 26-21, 26-24, 26-39 Problems 26-54, 26-63

Objective 10 D.C. Circuits a) Given a set of resistors in a series-parallel configuration; i) explain how current is divided among the resistors;
ii) calculate the equivalent resistance of the set. b) Given a circuit consisting of voltage sources and resistors; i) calculate the current & power supplied by the sources;
ii) calculate the current through, the potential drop across, and the power dissipated by any given resistor in the circuit. Suggested Study Procedure

Study Sec. 27-1 and 27-2 and Examples 27-1 and 27-2 where Young shows how a complicated

circuit can be simplified to become an equivalent circuit with a single resistor and single source of emf.

Exercises and Problems Related to Objective 10 Exercises: 27-1, 27-2, 27-5, 27-8 Problems: 27-43, 27-45 Objective 11 Multiloop Circuits Solve multiloop circuit problems using Kirchhoff's Rules. Study Sec. 27-3 and Examples 27-3 through 27-7. There are other methods of solving multiloop circuits (as EE's will learn), however Kirchhoff's Rules represent the most fundamental as they embody conservation of charge (the Junction Rule) and conservation of energy (the Loop Rule). Exercises and Problems Related to Objective 11

Exercises: 27-17, 27-18 Problems: 27-47, 27-51

Objective 12 Magnetic Forces

a) For two vectors given in i j k notation, calculate the vector product (cross product).

b) Define magnetic field.

c) Given the charge, mass, and initial velocity of a particle traveling through specified electric and magnetic fields, determine the force or the acceleration of the particle.

d) Given the current in a wire located in a magnetic field, determine the force experienced by each unit length of the wire.

Suggested Study Procedures

Study Sec. 28-1, 28-2 and 28-3. The diagrams in the margin of pp. 868 and 869 are important and so is Example 28-1. While we did not emphasize electric flux (found in Chapter 23), we will be emphasizing magnetic flux, so refer back to Chapter 23 if it helps. Make sure you can do Example 28-2.

Study Secs. 28-5 and 28-6 paying particular attention to Example 28-3. Sec. 28-7 lays the foundation for understanding the forces that current carrying wires experience in a magnetic field. Study it and Examples 28-7 and 28-8 carefully.

Suggested Exercises and Problems Related to Objective 12

Exercises: 28-1, 28-2, 28-3, 28-7, 28-15, 28-16, 28-23, 28-27

Problems: 28-39, 28-41, 28-42, 28-52, 28-53

HOMEWORK ASSIGNMENTS FOR STUDY GUIDE 3

Homework Assignment #9 - due in lecture Monday, Nov. 24

Problem 1. A lightning rod in a colonial home in Warren, Mass. is made of copper and has a diameter of 1.20 cm and a length of 0.750 m. During a lightning stroke, the rod carries a current of 5.0 x 10 ⁴ A. a) Calculate the resistance of the rod.
b) Calculate the potential drop along the rod.
c) Calculate the electric field in the rod, assuming it is uniform.
d) Calculate the power being dissipated in the rod while carrying the large current.
Problem 2. You are given the following resistors - R = 2W , R = 3W , R = 5W , R = 6W . a) Draw a circuit diagram indicating how you would connect them to get the largest equivalent resistance. What is the value of this largest equivalent resistance?
b) Draw a circuit diagram indicating how you would connect them to give the smallest equivalent resistance. What is the value of this smallest equivalent resistance?
c) Draw a circuit diagram indicating how you would connect them to give an equivalent resistance of 8.50 ohms. Homework Assignment #10 - due in lecture Monday, Dec. 1

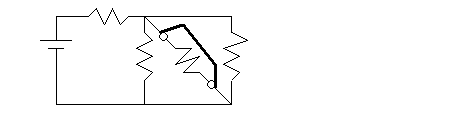
1) Problem 27-10 in Young. plus a conducting wire is now connected across R₃ as shown

c) Find the equivalent resistance of the network.

d) Find the current in each resistor.

2) Problem 27-46 in Young, but the current in one of the 16W resistors is given as 1.2 A from left to right rather than the current in the 8.0 A resistor as stated.

Homework Assignment #11 - due in lecture Wednesday, Dec. 3

Two batteries with internal resistances are connected as shown below.

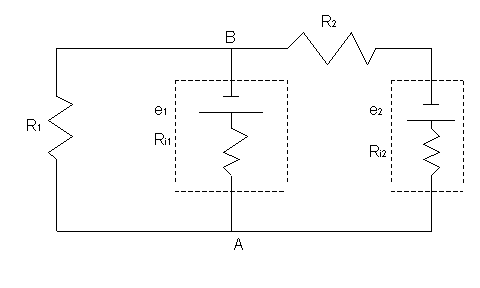
R₁= 0.40 W ; R₂= 0.25 W ; R_i1= 0.025 W ; R_i2= 0.020 W ; e ₁= 9.0 V; e ₂ = 4.0 V

a) Determine the current through R ₁ .

b) Determine the current through R ₂ .

c) What would a voltmeter read if it were connected between A and B. Indicate which point, A or B, should be connected to the positive terminal on the voltmeter.

d) Suppose a conducting wire is connected from A to B. Now what is the current through R₁ and R₂?

Homework Assignment #12 - due in lecture Friday, Dec. 5 1) In Cambridge, Mass, the magnetic field of the Earth has a vertical (down) component of 0.55 x 10 ^-4 T and a horizontal (north) component of 0.17 x 10^-4 T. What are the magnitude and direction of the magnetic force on an electron of velocity 1.0 x 10 ⁶m/s moving (instantaneously) in a west to east direction in a TV tube? Make sure you draw a diagram showing your directions of North, South, East, West, Up, and Down.

2) Young, Problem 28-54.