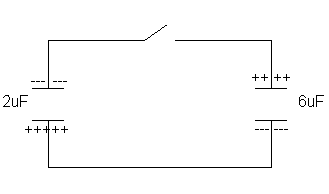PH 1120 Term B, 1996

PH 1120 Term B, 1997

STUDY GUIDE 2

Chapter 23 introduces Gauss's Law. After making a precise definition of "flux of a field", Gauss's Law states that the total flux of the electric field out of a closed surface equals the net charge contained within the closed surface (times a constant).

The flux of a field may be "very loosely" described as the "amount" of field cutting a surface; so Gauss's Law makes the very reasonable sounding statement that the amount of field coming out of a closed surface is proportional to the amount of charge contained within the closed surface. To make this reasonable statement usable the flux must be defined mathematically, something we will do later when we study magnetic fields.

One useful result obtained from Gauss's Law is that the field outside a spherically symmetric charge distribution looks just like that of a point charge located at the center of the spherically symmetric distribution. With this introduction you can read and understand some of Sec 23-5 and 23-6 describing the electric field in and around charged conductors.

Objective 4 Electric Potential Energy i) Calculate the work one must do against electrical forces in moving a point charge between two points in a uniform electric field.
ii) Calculate the work one must do against electrical forces in moving a point charge between two points in the vicinity of another point charge.
iii) Calculate the work one must do in assembling a given arrangement of two or more charges. Suggested Study Procedures Study Sec. 24-2. Please note that the lecturer may emphasize the work that you do against the electric force while the textbook describes the work done by the electrical force. One is the negative of the other. Study carefully Examples 24-1 an 24-2. Note that Example 24-1 applies the principle of conservation of energy in a way similar to what is done in mechanics when there are no nonconservative forces doing work. Exercises related to Objective 4 Exercises: 24-1, 24-5, 24-8 Objective 5 Electrical Potential i) Define electric potential. Calculate the potential difference between two points in a uniform electric field. Calculate the "absolute" potential which exists at a specified location in space due to: a) a stationary point charge, given its value and location
b) two or more stationary point charges, given their respective values and locations. ii) Calculate the potential difference between two points, given the value of a charge and the work involved in transporting it between the two points.
iii) Determine the motion of a charged particle accelerated through a known potential difference in a uniform electric field.
iv) Apply conservation of energy (kinetic and electrical potential) to problems involving charged particles moving in electrostatic fields. Suggested Study Procedures Study Sec. 24-3. Young defined potential in terms of a point charge. He then describes potential difference (a physical quantity used frequently) by equation 24-13. There is an alternate way of defining it which might be easier to understand. Potential difference can be defined as: the work that you do against electric forces in moving a positive charge (+q) from point a to point b divided by +q, at constant speed.

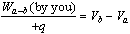Study the four examples: 24-3 through 24-5 and 24-7. An interesting example of charges moving through uniform electric fields is described in Sec. 24-7. Suggested Exercises and Problems Related to Objective 5 Exercises: 24-13, 24-15, 24-17, 24-25, 24-27, 24-38, and 24-39.

Problems 24-54, 24-56

Objective 6 Potential and Electric Field Given an electric field configuration be able to construct equipotential lines and given a configuration of equipotential lines, be able to construct electric field lines associated with the equipotentials. Suggested Study Procedures Study Sec. 24-5. Note how this relates to your laboratory experiment. It might be useful to review Example 24-10 since this also relates to the same experiment. Objective 7 Capacitance

a) Define capacitance
b) Given a set of capacitors in a series-parallel configuration, connected to a voltage source:

i) calculate the equivalent capacitance of the set;

ii) explain how charge is distributed among the capacitors, and how the potential changes across each capacitor;

iii) calculate the charge stored on each and the potential drop across each capacitor.

Suggested Study Procedures

Study Sec. 25-1 through 25-3 giving particular attention to Examples 25-1, 25-2, 25-5, and 25-6.

Suggested Exercises and Problems Related to Objective 7

Exercises: 25-1, 25-9, 25-11, 25-14, 25-15 Problem 25-43 Objective 8 Capacitors and Energy, Electric-Field Energy

a) Calculate the electrostatic energy stored in charged capacitors.

b) Calculate the final electrostatic energy in capacitors which have been initially independently charged and then connected together.

c) Calculate the energy density in an electric field.

Suggested Study Procedure Study Sec. 25-4. The derivation leading to the expressions (25-9) is important. Make sure you can do problems similar to Example 25-7. Read Sec. 25-5 and 25-6 to learn a bit more about capacitors than we are covering in this course. Suggested Exercises and Problems Related to Objective 8 Exercises: 25-17, 25-26 Problems: 25-37, 25-44, 25-46 HOMEWORK ASSIGNMENTS FOR STUDY GUIDE 2

Homework Assignment #5 - due in lecture Wednesday, Nov. 12

Exercise 24-12

Exercise 24-24 parts a) and b)

Homework Assignment #6 - due in lecture Friday, Nov. 14

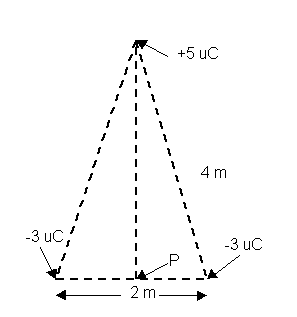
a) Calculate the work you must do to assemble the three charges at the corners of the isosceles triangle.

b) Calculate the work you must do to bring a charge of - 2 m C from very far away up to point P.

c) Suppose the - 2 m C charge is released from rest from point P. Describe clearly in what direction the charge would move (if it would move at all). Explain why it would move in that direction.

2) Young Prob. 24-17 with point A still on the line joining q₁and q₂ but is 0.025m from q₁ (and 0.075m from q₂ ).

Homework Assignment #7 - due in lecture Monday, Nov. 17

Two capacitors, with values 2.0 m F and 6.0 m F, are initially charged to 24 V by connecting each, for a short time, to a 24 V battery. The battery is then removed and the charged capacitors are connected as shown in the diagram. By closing the switch, the positive terminal of each capacitor connected to the negative terminal of the other.

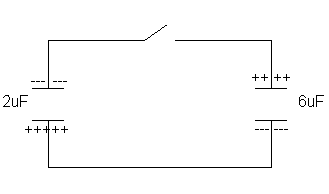Convince yourself that, after the switch is closed, the charges on the two capacitors will rearrange
themselves until the potential across each is the same.

a) Before the switch is closed, find the sum of the charges on the bottom two plates.

b) After the switch if closed, will the total charge on the bottom two plates be the same as, larger than, or smaller than it was before the switch is closed? If it changed, where did it go?

c) Calculate the energy stored in each charged capacitor before they are connected together.

d) After the switch is closed, what will be the final charge on each?

e) After the switch is closed, what will be the final voltage (potential difference) across each?

f) Calculate the fraction of the initial energy (stored in both capacitors) "lost" as a result of their being connected as shown.

Homework Assignment #8 - due in lecture Wednesday, Nov. 19

Consider the diagram shown.

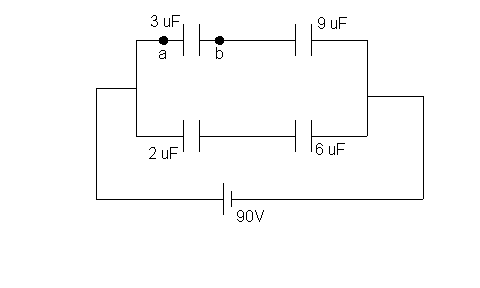
a) Find the equivalent capacitance of the system.

b) Calculate the potential across each capacitor.

c) Calculate the charge on each capacitor.

d) Calculate the total energy stored by the group.

Suppose now points a and b are connected by a conducting wire.

e) Find the potential difference across the 3 m F capacitor.

f) Find the potential difference across the 9 m F capacitor.

2. Exercise 24-25, but the potential difference between plates is 1.20 x 10⁺³ V.