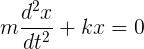
Today you are going to be experimenting with the DAMPED mass-spring oscillator. The motion of a simple harmonic oscillator is governed by the differential equation
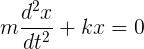
which has as its solution
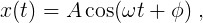
a simple sinusoid that can be completely characterized by three parameters: the amplitude A, and angular frequency ω, and the relative phase φ. The A and φ parameters depend on the initial conditions of the oscillation, but ω depends on the characteristics of the oscillating system itself. In the case of the mass-spring system,
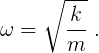
If the system experiences a damping force from viscous fluid, the above differential equation needs an additional drag term, casting the equation into the form of damped simple harmonic oscillation
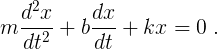
The addition of this one little term leads to the solution
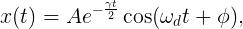
where
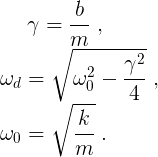
Because we now have more than one ω to worry about, we use subscripts to distinguish between the undamped angular frequency ω0 and the damped angular frequency ωd.
At your station there is a tall ring stand with a Vernier Dual-Range Force Sensor attached to a cross-bar located up near the top. Make sure that the Force Sensor switch is set in the ±10 N position. There is also a Vernier Motion Sensor looking straight up at the Force Sensor from its position on the lab bench directly underneath the Force Sensor. Also at your station you should find two springs, three circular cardboard damping disks, a 50-g mass hanger, and several slotted masses (one 50-g, five 100-g, two 10-g, one 5-g, two 2-g, and one 1-g masses). Note that numbers on the damping disk are it's radius in cm. You want to label your data by the radius of the disk to keep organized.
First measure and record on your Data Sheet the mass (to the nearest gram) of each of the three damping disks using a mass balances located around the room.
Hang the two springs in a series arrangement from the hook at the bottom of the Force Sensor, and from the bottom end of the bottom spring hang the empty mass hanger. Damp out any motion of the hanger so that it provides a nice stable reference plane for zeroing the Motion Sensor.
Open the Logger Pro File SpringConstant. Continue as you have done before to determine the spring constant. As always it is important to handle the masses with care above the motion sensor.
Now close the Logger Pro File SpringConstant and open the Logger Pro File Fit Oscillations. Adjust the mass hanging from the bottom spring to 400 g plus the extra mass equals to the mass of the heaviest damping disk (to the nearest gram). For example, if the heaviest disk weighs 17 g, you have to make the mass plus the hanger 417 g. With the hanger motionless, zero the Sensor readings. Then pull the mass hanger straight down a distance of about 5 cm and release it. When you are satisfied that you have released it in such a way that the motion is mostly up-down and very little side-to-side, collect the oscillation data. After you wait patiently for some 10 seconds, data collection will end. Shortly thereafter the curve fit data box will open with angular frequency displayed as the "B" parameter. Record ω to 4-digit precision on your Data Sheet.
Open the Logger Pro File Damped Oscillations. Remove the extra mass on the hanger (the 17 g in this example). Then, put the disk on the hanger such that it is in the middle of the masses to prevent the disk from moving around. (You will have to remove some masses and put them back on top of the disk.) Note that when you work on the other disks (which are lighter), you need to add more masses such that the total mass of the hanger and disk is equal to 400 g plus the mass of the largest disk.
Zero the reading, then pull down the mass hanger about 5 cm and release it. Once the system is oscillating smoothly up and down, start collecting data. The template records hanger-position data for 100 seconds. If you want to resize the amplitude at the end of the data collection, you can click anywhere in the graphical region to select that graph and autoscale it.
First you are going to try fitting the first 20 s of position data. First move the cursor around near the 100 on the time axis and click. Enter the number 20 in place of 100 and hit “Enter”. Now the position data between 0 and 20 seconds should be displayed on the graph. Note that the individual oscillations are spread comfortably apart.
Now, perform a curve fit. Select “Damped Sinusoidal” from the list labelled “General Equations” in the lower left corner. You will notice the five parameters for this fit routine are labelled A through E
At this point you are going to set the five fitting parameters closer to their proper values to be consistent with the 20-s graph that appears at the upper left of the “Curve Fit” box. Set the parameters as follows: D= 0, B= value from Part 1, A= approximately the starting amplitude of the graph. Now, reduce the damping parameter, E so that the black curve falls off at about the same rate as the red graph. Finally, adjust the relative phase C so that the black and red curves are close to overlapping (change the C-parameter from 1 to 2 to other integers until you get close to overlap). At this point, you may want to adjust some of the already-adjusted parameters, BUT it doesn't need to be perfect.
When you are finished with your adjustments, check the “Automatic” box up near the top, and then click on “Try Fit”. After some waiting, the best-fit black theoretical curve will be superimposed on the red experimental curve. If the fit has slid off convergence to a bogus set of values that obviously does not fit very well, you will have to try again, this time by setting the A through E parameters for a better initial match. But once the computer has given you a proper set of fitting parameters for a good fit, click on the “OK” button for a full-screen view of what will likely impress you as a rather spectacular fit, and then write down the A through E values on your Data Sheet for subsequent use (include the uncertainty only for E).
Now you are going to perform the same fitting exercise, except now on the region 80 to 100 s. At this point, we want you to perform a computer fit on the 80 -100 s region, just as you did before. Note how the parameters change from before. When you have achieved a reasonable fit, switch to “Automatic”, click “Try Fit”. Once you obtain a good fit, write down these fitting parameters A - E.
Repeat again the process one last time, from 30 to 70 s.
During fitting, you are encouraged to manually play with the parameters and observe the change in the fit to get a feel of how each parameter dictates the characteristic of the oscillation.
You are expected to measure and compare the drag coefficients of the three disks. Do the results match your expectations, and why?