In this experiment you will continue your study of the mass/spring oscillator. As with the previous experiment, this experiment will be divided into two parts. In Part 1, you will again measure the spring constant of one individual spring, and then you will measure the spring constant of a somewhat complicated arrangement of 4 similar springs. In Part 2, you will measure the period of oscillation of two mass/spring systems, one with that somewhat complicated arrangement of 4 springs, and the second with the same individual spring you used at the beginning of this experiment. In Part 2, you will further explore the interrelationships among the motion parameters—x, vx, and ax—and their relationships with the suspending force of the Force Sensor that keeps the mass/spring system oscillating around a fixed equilibrium point.
In this first part of the experiment, you will be measuring the spring constant of 1 individual spring plus a somewhat complicated arrangement of four similar springs for which you will need the individual spring force constants.
At your station there is a tall ring stand with a Vernier Dual-Range Force Sensor attached to a cross-bar located up near the top. Make sure that the Force Sensor switch is set in the ± 10 N position. There is also a Vernier Motion Sensor looking straight up at the Force Sensor from its position on the lab bench directly underneath the Force Sensor. Also at your station you should find four springs, a 50g mass hanger, and several slotted masses (1 50g and 9 100g).
Open the Logger Pro File for Part 1 and proceed to measure the spring constant as you have done before.
While measuring the effective spring constant for the four spring configuration, use the same Logger Pro template as before, but this time zero the two sensors with the mass hanger PLUS 50 g hanging from the spring arrangement (Why?). Then after zeroing, begin measuring force versus extension with another 100g mass added for a total hanging mass of 200g. Collect data at 200g intervals, up to 1000g, and determine the spring constant.
Note that because all four springs have approximately the same spring constant, the spring constant for the series-parallel arrangement is about the same as for a single by itself. (In Experiment #1, you learned the rule for determining the spring constant of two springs in series—the reciprocal of the series spring constant is simply the sum of the reciprocals of the individual spring constants. Turns out that the net spring constant of springs in PARALLEL is simply the SUM of the spring constants for the two spring arrangements in parallel.)
Now that you have determined the spring constants of a couple of different spring systems, it's time to use each system to study the motion of these systems in oscillation.
Open the Logger Pro File for Part 2. Since your system is already set up with the complicated 4-spring arrangement, keep that arrangement, but load the 4-spring arrangement with a total of 600g. Note that this template will display the force measured by the force sensor plus all three of the motion parameters—x, vx, and ax.
Again, zero the readings, then displace the mass hanger a centimeter or two from equilibrium and release it to oscillate. Make sure that the amplitude of oscillation is not so great that the springs can close to their compressed coil-to-coil length. Once you are satisfied that the mass/spring system is oscillating smoothly up and down with little side-to-side motion, click on collect, and wait approximately 10 seconds. As in the previous lab, the program automatically stops the data collection at this time. You may want to scale the results for your convenience.
Once collection stops and the data are displayed, click on the Force Sensor graph to select that data, place the cursor at the very top of the right-most peak, and read the time coordinate off the coordinate meter. Then move the cursor to the very peak of the left-most peak and read its time coordinate. Remember pur discussion concerning Zero crossings of the X-axis. Determine the period of motion. The period of motion is given by
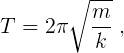
where m is the total mass hanging on the spring and k is the spring constant of the spring system. Determine the theoretically-predicted value for the period, and write down both that and your experimentally-measured value.
Remove the mass hanger and springs from the Force Sensor, take the springs apart (placing a single spring back on the Force Sensor), and repeat the above oscillation experiment with 300g hanging from that single spring. In the manner described above, determine the period of oscillation for this new arrangement, then calculate the theoretically-predicted value. If the agreement in either case is not better than 1% or so, call your lab instructor over to look at your work to see what might be wrong.
Now select all four graphs simultaneously by depressing the Shift key and then left-clicking on each of the four graphs. Next examine all four graphs at once. By moving the cursor left and right, you can control the position of each of the four measuring lines so as to compare the relative phases of each graph. Two of the graphs always peak at the same time—which two are these?
Your lab instructor will give you additional comparisons to make among these four graphs.