You will use Vernier equipment to measure the value of a carbon resistor, complete with uncertainty. Our interest in the carbon resistor is not so much based on its ubiquitous presence in essentially every electrical circuit ever designed, but on its linearity; the fact that the voltage difference across a carbon resistor is linearly proportional to the current flow through the resistor. This relationship is known as Ohm’s law: V = IR, where V is the voltage across the resistor (measured in volts), I is the current through the resistor (measured in amperes, or simply, amps), and R is the resistance of the resistor (measured in ohms = volts/amps = V/A = Ω). The magic of the carbon resistor is that its resistance value R is remarkably constant over its whole operational range of applied voltages and resulting currents. Basically, you will be using this constant resistance property of the carbon resistor as a vehicle for learning a bit more about the meaning of measurement uncertainties and a bit more about how uncertainties are handled in real-world measurement situations.
Important note: Be sure never to exceed 6.0 V across the Vernier Differential Voltage meter or 0.6 A through the Vernier Current meter, as read on their respective meters in the Logger Pro template used in the following experiment.
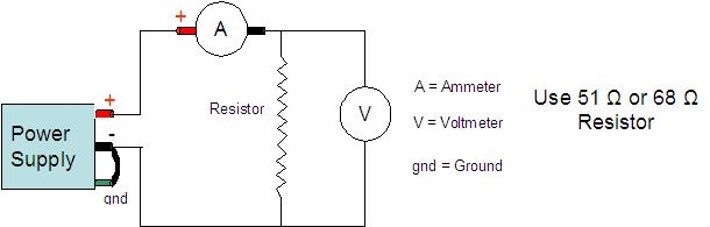
You are going to determine the resistance of a carbon resistor by making electrical voltage and current measurements using Ohm's Law.

First connect up the circuit as described on the white board by your lab instructor. After opening the Ohm's Law Logger Pro template, you should zero the reading, after making sure that the voltage supply is set to zero. Begin collecting data, then record 9 datum points (via the Keep function) that appear on the I-V graph, starting with a voltage of 0 and increasing by approximately 0.5 V increments up to a maximum value of 4.0 V. After recording the 9th point, stop data acquisition.
The resistance value is the slope of the best fit line through the set of these 9 data points. Logger Pro can calculate the best fit line and tell you the parameters. Please note how closely the nine points come to fitting a perfect straight line; a testament to how constant the resistance of a carbon resistor is over a range of voltage/current values. Be sure to record the uncertainty to five digits. Once the data are recorded on your data sheet, select "Data" from the main menu choices and click "Clear All Data".
Record three more data sets in the same manner. It would be wise to zero the readings before each set is gathered (after you set the voltage back down to zero).
Open the standard deviation calculator and enter the four 5-digit slope values where indicated and you will automatically be given the average and standard deviation of that set of four resistance values, which you should transcribe on your Data Sheet. If your experiment was properly and carefully performed, you should find that the calculated standard deviation of the 4-element data set is of the same order of magnitude as the individual slope uncertainties recorded from each individual experiment, and any difference between an individual resistance and the average resistance is less than twice the sum of the total uncertainty and the individual uncertainty (Check this. Why is this true? Think about Normal distributions!).
Technically, the average and standard deviation of a set of several identical repetitions of the same measurement (especially if the repetition number is far greater than four) is the most correct statement of the "true" slope value, but this experiment is intended to show you that one measurement with uncertainty can provide roughly comparable information! And briefly stated, this linear fitting approach is a common way that data are analyzed out in the real world. In subsequent experiments you will be using this approach to accomplish some significant data analysis, so please don’t promptly forget everything you did or learned today! You will need to apply it all again soon!
In Part 2, you will be measuring the resistance of two different carbon resistors plus two combinations of those resistors: a series and a parallel combination. Note below that you will extend this exercise to more than 2 resistors in order to experimentally demonstrate the known expressions for adding resistors in series and parallel. You will be measuring resistances just as you did in a previous Experiment, where you found that one careful set of measurements of potential versus current values gave a highly precise determination of resistance together with a measure of the resistance uncertainty.
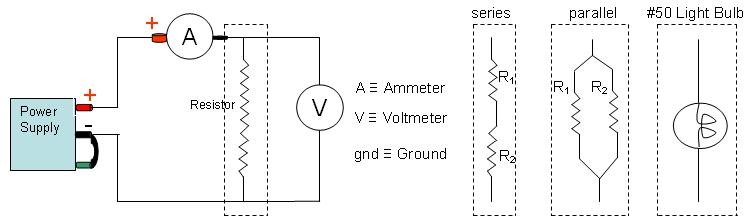
Hook up a circuit in a similar manner to what you have done for measuring the resistance of one of the 51 Ω carbon resistors on the Vernier circuit board. Once you are certain that your circuit is properly hooked up, check that the voltage-adjust knob on the power supply is turned fully CCW and then turn the power supply ON. Open the Ohm's Law Series and Parallel template, and then zero the reading. When the "Zero Sensor Calibrations" box opens, click OK, and then collect data.
Record nine datum points starting from (0,0) and then increasing the voltage setting successively from 0 to 4V by approximately 0.5V increments. After turning the voltage-adjust knob to the next desired voltage level, wait a couple of seconds to let the system settle down to its new current-voltage state before clicking the "Keep" button. When you have collected a total of nine V vs. I points, stop data collection. Be sure to turn the voltage-adjust knob fully CCW to the zero position at this point.
Perform a linear fit for your 9 datum points. Open "Linear Fit Options" from the Logger Pro menu, and then select "5 significant figures" and "Show Uncertainties". Record (on your Worksheet) the slope and uncertainty of the linear fit to your 9 points with all digits, just as they appear in the data box; for the time being you will keep all digits for subsequent calculations. If you did everything properly, you should find that the slope-value (the resistance of the carbon resistor) has an uncertainty of only about 0.2% or less! (In the aggregate, these resistors are only specified to a 5% range above and below the nominal value of each resistor printed on the circuit board.)
Move the clip leads from the connection posts of the 51 Ω resistor to those of one of the 68 Ω resistors. Click the "Data" choice up on the main menu bar, and select the "Clear All Data" choice at the very bottom of the list that appears. Do NOT close the least squares data box that then becomes empty. Repeat the steps above involved in recording 9 datum point with which you will determine the resistance and uncertainty of that resistor, and record resistance and uncertainty on your Data Sheet, again writing down all available digits. Once complete, repeat with the resistors arranges in series and then in parallel configurations. We will refer to these four resistance values, in order, as R1, R2, Rs, and Rp, etc.
Part of your challenge for this part of the resistance Lab work will be to experimentally demonstrate the Mathematical equations which you already know for how resistors add in Series and in parallel. For this purpose we have supplied a large collection of resistors of different values that you should use for this purpose.