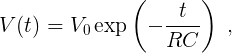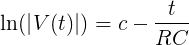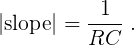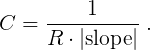PH 1121 Lab 2: Capacitance
Introductory Comments
The resistance of carbon resistors is relatively easy to measure, as you will discover in a subsequent sequence of experiments. The direct measurement of capacitance requires special equipment that we are not going to duplicate at our lab stations. You are going to use a special approach especially suited to our Vernier equipment, with the emphasis on measuring the equivalent capacitance value of parallel and series combinations of capacitors as discussed in lecture. Note that the voltmeter is connected "across" the capacitor; it is in parallel with the capacitor.
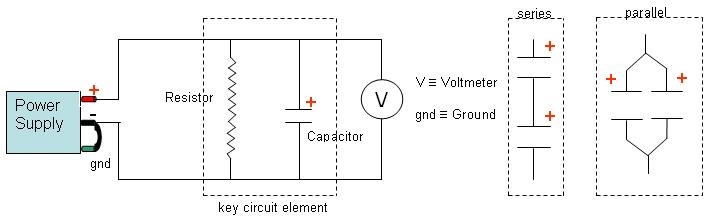
As you will hear in lecture, a charged capacitor connected to a resistor discharges through the resistor in such a way that the voltage across the capacitor decreases with time according to the equation
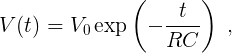
where V0 is the initial voltage across the capacitor at time t = 0, R is the resistance value of the resistor, and C is the capacitance value of the capacitor. LoggerPro is able to plot both V(t) and
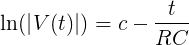
for some constant c. Whereas V(t) is an exponential, the natural log of the absolute value of V(t) is a straight line of slope magnitude
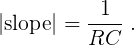
You will be using an R = 22,000Ω ± 5% resistor in this experiment, and you will be measuring the slope of the natural log of the time-varying voltage across the capacitor, which means that you can solve for C as
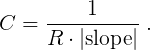
Note on capacitors: the short wire is the negative wire, and this wire must be connected closer to the negative terminal of the power supply. Additionally, there are arrows on the side of the capacitor showing the direction current is supposed to flow in.
Procedure
- Hook up the circuit with only one capacitor connected in the circuit as described by your Lab Instructor. BE SURE to connect the capacitor into the circuit properly with the + end (if the capacitor has a polarization preference) connected to the positive side of the voltage supply. Open the LoggerPro template and turn on the power supply (making sure that the voltage control knob is turned CCW all the way to its zero position). Now. zero the reading and then turn up the voltage of the power supply until the voltage meter reads about 5.0 V. Start collecting data and quickly prepare to disconnect the + voltage clip lead from the circuit once the "Collect" button turns red and you see data begin to collect, forming horizontal lines on the graph. As soon as you disconnect the + voltage, the capacitor will begin to discharge through the resistor, and you will see the two voltage graphs being recorded suddenly change profiles; one following an exponential profile with time, while the other follows a downward-sloped straight line. Data collection automatically stops after 10 seconds. You should turn down the voltage supply to 0 at this point.
- Highlight from near the top of the downward-sloped straight line to a point where that graph begins getting noisy, and perform a least-squares fit. When the "Select Columns" dialog box opens deselect the "Latest Potential" choice so that only straight-line graph will be involved when you close the dialog box. Then right click the least-squares data box so that you can select the "Linear Fit Options" where you will select 5 significant figures and "Show Uncertainty". Write down your slope magnitude and uncertainty values (See Note Below). The reciprocal of the quantity "slope magnitude" times 22,000 Ω gives the value of the capacitor in farads (F), the SI unit for capacitance. Note: What you should do for uncertainty in capacitance is simply to calculate the 4 capacitance values, using the slope magnitudes and 22,000 Ω. Take 5% of each resultant as the uncertainty, and then express each capacitance value in industry-standard format.
- Now repeat the experiment with the first capacitor replaced by the second capacitor found at your station, then both in parallel, and finally with both in series. Be careful to connect the positive side of the capacitor (if polarized) to the positive side of the voltage supply and zero the reading (with the voltage supply still at zero) between each experiment.
- We have many capacitors with nominally the same value. Part of your challenge in this experiment is to use sufficient numbers of capacitors in series and parallel so that you can experimentally demonstrate the known mathematical expressions for how capacitors add in series and in parallel.
Back to PH 1121 Labs
Back to Main Page