Introduction The North American Free Trade Agreement was signed by the United States, Canada and Mexico in 1992 and put into effect in 1994. It removes tariffs and other trade restrictions between the countries, effectively creating the world's largest open economic market (the other large market, the European Economic Community, also went into effect in 1994).

Workers in the United States had concerns as they feared jobs they held would be moved to Mexico where pay is much less. Some companies had concerns about losing business to lower priced Mexican companies who, in addition to paying lower wages, also have less stringent environmental regulations to comply with. On the plus side, the move opened up previously protected markets such as those for electronics, automobiles and food, to American and Canadian companies. The long term effects remain to be completely seen, but are probably less significant than originally feared.

Aside from movement of jobs and changing of markets, prices may also rapidly change. If a company has little competition, then its price may be "all the market can bear". If it all of a sudden has a foreign competitor with substantially lower prices, then a period of adjustment will ensue, with changes occurring for both companies. This happened in the auto industry in the 1970s, for example.

It is also helpful to compare the US, Canadian and Mexican economies in some basic areas as they have some fundamental differences in terms of magnitude:

                                       US          Canada            Mexico

      GDP (billions)          $5,465          $513               $187

  population (millions)        250           26.6                  86

  per capita GDP        $22,000       $21,500              $2,500                        (1990 data)

(source: World Bank World Development Report, 1992)

In this project, we examine how price stabilization in the NAFTA era may be mathematically studied using work originally developed by Nobel Prize winner Wassily Leontief.

Background section 8.5 of Kolman, linear economic models. We assume the reader is familiar with this material, particularly page 465.

Here we assume that there are three countries, the United States, Canada, and Mexico, in that order. Further, A denotes the 3x3 exchange matrix (nonegative, columns add up to one).

Next, suppose that p = (y₁,y₂,y₃)^t is a 3x1 column vector where y_i is the price that nation #i charges for its goods, as a group, that are exchanged on the open market between the three nations. Following Kolman, the linear combination

               a₁₁y₁ + a₁₂y₂ + a₁₃y₃

is the monetary sum of goods sold within the United States and total imports bought by the United States from Canada and Mexico. Similarly,

               a₂₁y₁ + a₂₂y₂ + a₂₃y₃

is the sum Canada receives from sales within Canada (a₂₂y₂) and exports to the US and Mexico. Finally,

                a₃₁y₁ + a₃₂y₂ + a₃₃y₃

is the sum Mexico receives from sales within Mexico (a₃₃y₃) and exports to the US and Canada.

In matrix terms, the column vector produced by the product Ap, represents income for each of the nations (recall p = (y₁,y₂,y₃)^t ). Now in a state of perfect equilibrium, the income for each nation would equal what it spent so no one would have a trade imbalance (especially a trade deficit). This would be represented, as in Kolman, by the matrix equation

                 Ap = p.

However, the prices, not being under anyone's control, cannot guarantee this. Thus one has

(where by "not equal", for matrices, it means that at least one component does not match up).

Now nations do not desire trade imbalances, so prices change over time. For the remainder of this project, we will let p(k) denote the price vector after k months of time have elapsed, indicating that we now have a dynamic situation.

The question we are interested in is: is this a stable or unstable economic situation? Will prices stabilize as a group, or will some grow or decline indefinitely? In the latter case, there are many negative ramifications. Finally, if they stabilize, can we predict what they will stabilize to?

In mathematical terms, we are interested in the existence and value of

In order to begin to answer this, we first need to know how the prices change over time. We will assume that at the end of each month, all nations agree to adjust prices so that their prices for the upcoming month equals their income from the current month. Mathematically, this means that

               p(k+1) = Ap(k)

If we denote the origin prices by p₀ , then one may solve this equation (which we have seen in a number of other situations) and find that

               p(k) = A^k p₀

Problems   Suppose in what follows that the exchange matrix is

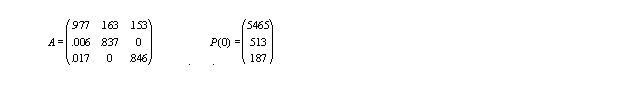
Write out your interpretation of all nine entries in the exchange matrix A.

In general, how can we use the model to tell if a nation has a trade deficit or surplus?

Suppose initially we take p₀ = (5465,513,187)^t (units of billions of dollars). What does the model predict that each nation will have for an imbalance of trade in 5 years? Assume in each case that their GDP increases annually by 2%. Be sure an indicate if the imbalance is a net surplus or deficit in each case.

If you were to write to your congressman and tell him whether you wanted him to support NAFTA or not, what would you tell him?

How does the Leontief model compare with the Markov chain model?

What effect does the act of devaluing a currency have on the situation?

References

Lustig, Bosworth, Lawrence, eds., North American Free Trade Assessing the Impact. 1992. Washington D.C. The Brookings Institution.