This project will acquaint you with population modeling and how linear algebra tools may be used to study it.

Background: Kolman, pages 305-307.

Population modeling is useful from many different perspectives:

1. planners at the city, state, and national level who look at human populations and need forecasts of populations in order to do planning for future needs. These future needs include housing, schools, care for the elderly, jobs, and utilities such as electricity,water and transportation.

2. businesses do population planning so as to predict how the portions of the population that use their product will be changing.

3. Ecologists use population models to study ecological systems, especially those where endangered species are involved so as to try to find measures that will restore the population.

4. medical researchers treat microorganisms and viruses as populations and seek to understand the dynamics of their populations; especially why some thrive in certain environments but don't in others.

In human situations, it is normal to take intervals of 10 years as the census is taken every 10 years. Thus the age groups would be 0-9,10-19,11-20 etc , so 8 or 9 age categories would probably be appropriate. The survival fractions would then show the fraction of "newborns" (0-9) who survive to age 10, the fraction of 10 to 19 year olds who survive to 20 etc. This type of data is compiled, for example, by actuaries working for insurance companies for life and medical insurance purposes.

The basic equations we begin with are

          (1) x(k+1) = Ax(k)           k=0,1,2,. . .      and x(0) given

with solution found iteratively to be

         (2) x(k) = A^kx(0)

(see Kolman for details of the structure of A, which is 7 x 7 in this case).

Your Project: Suppose we are studying the population dynamics of Los Angeles for the purpose of making a planning proposal to the city which will form the basis for predicting school, transportation, housing, water, and electrical needs for the years from 2000 on.

As above, we take the unit of time to be 10 years, and take 7 age groups: 0-9,10-19,...,50-59,60+. Suppose

further that the population distribution as of 1990 (the last census) is

          (3.1, 2.8, 2.0, 2.5, 2.0, 1.8, 2.9) (x10⁵ )

and that the Leslie matrix,A, for this model appears as

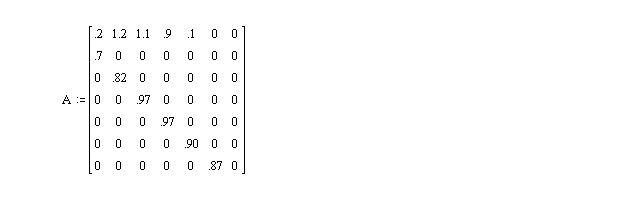
Part One: interpret carefully each of the nonzero terms in the matrix. In addition, indicate what factors you think might change those numbers (they might be social, economical, political or environmental).

Part Two: Predict:

* what the population distribution will look like in 2000, 2010, 2020 and 2030

* what the total population will be in each of those years

* by what fraction the total population changed each year

Additionally, what does your software tell you the largest, positive eigenvalue of A is?

Part Three: Decide if you believe the population is going to zero, becoming stable, or is unstable in the long run. Be sure and describe in your write up how you arrived at your conclusion.

If you have decided it is unstable, simulate it long enough that the column matrices for two successive populations are proportional to one another. Calculate that proportionality factor to one decimal place and report it.

Part Four: suppose the birth rates for the second age class can be reduced by 25% by the year 2000. How does that change your predictions for 2010,2020 and 2030? Is the population still unstable?

Part Five: How does the basic model change if immigration is introduced? Suppose we assume that a constant number of immigrants are added to each age group during each time interval. What will equation (1) now look like?

What will the solution, (2) now look like? (do this by hand)

How do your predictions change for 2000, 2010, 2020, and 2030 change if there are 20,000 people entering each age group during each 10 year period? How much will the total population have changed in 2030 as compared to the prior no immigration prediction?