WORCESTER POLYTECHNIC INSTITUTE
TWENTIETH ANNUAL INVITATIONAL MATH MEET
OCTOBER 17, 2007
TEAM EXAM QUESTION SHEET
- A ball was floating in a lake when the lake froze. The ball was removed (without breaking the ice), leaving a hole 24 cm across the top and 8 cm deep. What was the radius of the ball in centimeters?
- Point of tangency of two spheres described by
x2 + y2 + z2 = 121
(x-4)2
+ (y-12)2 + (z-18)2 =
121
- Consider the graphs of y = Ax2 and y2 + 3 = x2 + 4y, where A is a positive constant and x and y are real variables. In how many points do the two graphs intersect?
- A
certain 5 digit number has the property that if a 1 is placed after it, it
is 3 times as large as with a 1 placed before it. What is that number?
- We
have two concentric circles and wish to find the area of the annulus
between them. If we draw a chord
through the outer circle tangent to the inner circle, its length is 20 inches.
What is that area?
- Factor the following polynomial over the reals as completely as possible:
![]()
7. If z = √2 +√2 i ,
what is z20 ? (where i = ![]() )
)
8. Simplify (a + b)15 mod 15.
- Simplify 3218 mod 7.
- Determine the file size in Megabytes (Mb) for a digital recording made with samples of
size 2 bytes taken 44,100 times per second, in stereo, for 40 minutes. Your answer
should be rounded to the nearest tenth of a Mb.
11. Find the sum 17 + 22 + 27+. . . +182.
12. If it is given that
logx
w=24 logy w =40 logxyz w = 12
then what is logzw ? (x,y and z are
all positive numbers)
13. Simplify the following to a single fraction
-5/4 + 5/8 –
5/16 + 5/32 . . . - 5/1024
14. Determine 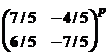 where p
is prime and positive.
where p
is prime and positive.