Worcester Polytechnic Institute
Department of Electrical and Computer Engineering
EE 2311: Continuous-Time Signal
and System Analysis
Discovery Project II — Signals
From Scratch
Note: this project was used
in 2000-2001. A new project is being assigned by Prof Vaz for B01. This
project is presented here as a vehicle for illustrating Fouier methods only.
Please see Professor Vaz if you need the new project for EE2311.
You have already traveled a fair way down the long and winding road of continuous-time signal analysis. You have learned the basics of how we measure signals, how we tell them apart, and how we can classify them. Also, you have learned about special signals, such as the impulse, that can make life a little easier in the time and frequency domains. You have even stared into the gaping maw of convolution, and witnessed what evil lies therein.
But now, you ask yourself, “If it takes me an hour to convolve a rectangular pulse with an exponential, how in the world will I ever be able to do anything more complicated??” One of the most important problems we have to solve in the world of communications is the age-old “input-output problem”—that is, how do we find the output of a given system, knowing the input? So far, however, the only way we have discovered to accomplish this task is through the rigors of convolution, performed in our own familiar time domain. But looking ahead, you think, “Convolution is such a pain…isn’t there a better way?”
And there is! It’s called Fourier theory, and if you haven’t heard of it already, it is a beautiful and elegant way to analyze signals and systems. To get to the root of this method, however, we need to know: what is it that makes up a signal? Just as one cannot understand chemistry without knowledge of the atom, in order to comprehend signal analysis, it is necessary to know how signals are built from basic elements. That is what this second project will examine—how do we actually build signals?
So, our objectives for this project will be:
· To present the basics of signal construction by examining the similarities between signals and vectors.
· To discover how mathematical operation of a vector dot product can be expanded into a “dot product” for signals.
· To define the quality known as orthogonality, for both vectors and signals.
· To explore a measure of signal similarity called correlation.
· To examine the use of an orthonormal basis—a set that can serve as the “atomic building blocks” of vectors or signals—for vector or signal construction.
· To utilize an orthonormal basis set to construct a signal, using Matlab.
Part 1: Vectors and Signals, Signals and Vectors
Dot Products and Vector Components
What is a vector? Mathematically, it is an abstract representation of a quantity with multiple dimensions. To represent this quantity, we may use an arrow (graphically), or an ordered set of values (numerically). Unlike scalar quantities such as temperature, vector quantities—things like displacement or force—must be represented in two or three (or possibly even more) dimensions. An important question, then, is to consider what makes a “vector” representation of a quantity so useful to us? One advantage is that we can break down these vectors into their components—their basic dimensional elements. By doing this, we can take two seemingly unrelated vectors (such as two forces pulling the same object in two unrelated directions), and combine them. We accomplish this by breaking each vector down into its set of components; effectively, we re-create the two different vectors as sums of differently scaled versions of the same standard set of vectors. Then, with the two vectors expressed in terms of the same kinds of components, we add up these separate parts of each vector that are related. If you have ever added two vectors in a physics class, then you have had experience with this operation before.
First, though, we have to define a vector operation that will be useful to us later—the vector dot product (also known as an inner or scalar product). The dot product operation is performed on a pair of vectors, and is denoted by a pair of angled brackets: <a, b> is read as “the dot product of vectors a and b”. (Note that vectors in this document will be denoted by boldface type, and that |v| will represent the length or magnitude of some vector v.) For any two vectors a and b with an angle of q radians between them,
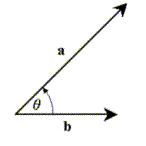
Figure 1: Finding the dot product of two vectors.
![]() , [Equation 1.1]
, [Equation 1.1]
and when a = b (the dot product of a vector with itself),
![]() . [Equation 1.2]
. [Equation 1.2]
Problem 1: What is significant about the dot product when two vectors are pointing in the same direction? What about when they are pointing in opposing directions? What does a dot product of zero tell us? Provide support for your arguments. [5 pts.]
So, how do we use the dot product, along with our knowledge of trigonometry, to find the components of a vector? Figure 2 shows a two-dimensional vector, denoted by v. As you may remember from physics, it is often the convention to break a two-dimensional vector into the sum of scaled versions of a standard set of two basis vectors, denoted by i and j. These two familiar vectors have some special characteristics that make them a very good foundation to form components. In fact, we refer to the vectors i and j as the “basis set” for the space of two-dimensional vectors. We will discuss the concept of a basis set in greater detail later; for now, let’s review how we derive the components of a vector.
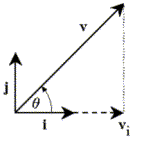
Figure 2: A vector and one of its components.
We should know already that given our “basis set” all we need to completely make up v is a certain scalar multiple of the vector i that we can add to a certain scalar multiple of the vector j. So, all we have to do to break up vector v into components is find out how much we need of each basis vector, correct? First, let’s try to find out how much of the vector v lies along the path of i. This will give us vi—known as the component in the i‑direction of vector v, or the projection of vector v along vector i. Performing some simple trigonometry on the vectors shown in Figure 2 gives us
![]() , [Equation
2.1]
, [Equation
2.1]
and thus
![]() . [Equation 2.2]
. [Equation 2.2]
Now, part of the benefits of using i and j as a basis set is that they are unit vectors. Since the length of each vector is unity, it makes it easier to express the component in the i-direction of v in terms of i. For instance, if we want to express vi in terms of i, then vi is simply |vi|∙i, since |i| = 1. We say that the basis vectors i and j have been normalized—but we will discuss this as well later on in the project.
We can use the unit length property of vector i to express Equation 2.2 in terms of the dot product. Since
![]() , [Equation
3.1]
, [Equation
3.1]
then
![]() . [Equation
3.2]
. [Equation
3.2]
However, what would be the case if the length of vector i were not unity? Figure 3 shows vector v again, but this time the vector we are using for part of the basis set is not of unit length (vector w). As before, we want to find out how much of the basis vector (this time, vector w) is used to make up v. However, we will ultimately want to express this relationship in terms of some constant c, which represents by how much we would scale the basis vector w to make it equivalent to the component of vector v along w.

Figure 3: Finding the component of a vector along another vector.
Now, stop and look at Figure 3 and think for a moment. We know that there is some amount of vector w, some scaled version of itself, that can contribute to making vector v—this has been drawn as vw. But in fact, we don’t have to use the vector vw as it is drawn above—we could use any amount of vector w in constructing vector v. No matter how long we choose to make vector vw, there would always be some other vector that we would have to add to vw to totally make up v. We can imagine this other vector—the leftover part of v that cannot be represented by vw alone—as the vector that we would add to the tip of vw , to get us back to the tip of v. This difference between vw and v is the error vector, represented above by the dotted line.
So if we could potentially use any amount of w to build v, then what’s the point? Well, by making the error vector as small as possible, we are creating the best vw—the perfect amount of w to try to make up v. Think of it as using vw to approximate v; the best possible approximation will occur when the error vector is the smallest. From the figure, it may appear that the perfect length of vector vw occurs when the error vector is perpendicular to our component (as it is drawn). And indeed, this is the case.
Perhaps it would help at this point to make a note about orthogonality. As was stated previously, the unit vectors i and j have a few different properties that make them an excellent basis for two-dimensional vector construction. One such property, which we have mentioned, is that they have been normalized. Another is that they are orthogonal. The mathematical definition of orthogonality is that if the dot product of two vectors equals zero, then the two vectors are orthogonal. Thus, if
![]() , [Equation 4]
, [Equation 4]
then vectors v and w are orthogonal. From Equation 4, you can see that orthogonality must occur when cos(q) = 0, or when q = 90°. In other words: perpendicular vectors are orthogonal. Why is this a good quality for a basis set to have? Well, since i and j are perpendicular (or orthogonal), the component of each vector in the direction of the other is zero, and thus neither vector can be made up of any part of the other. And since we’re trying to build vectors from elemental parts, you can hopefully see the sense in requiring that these elemental parts are not at all made up of each other, as that would get kind of confusing.
Problem
2: Figure 4(a) shows a vector v, whose magnitude |v| =
4.50. Also shown are the unit vectors a and b, with qa
= 102° and qb
= 31°, which we will use a basis set for constructing v. Is it possible for us to
express v as a sum of scaled
versions of a and b?
(Think carefully.) Find the
projection of vector v in the
direction of each vector. Will these
projections add up to form v? Perform this same set of operations on v again, this time using the basis set
shown in Figure 4(b), with qi = 53° and qj = 37°. Compare and contrast our two sets of basis vectors: how are they the same, and how are they
different? [10 pts.]
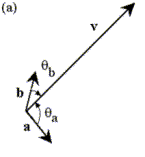
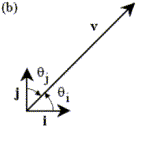
Figure 4: Vectors and basis sets for Problem 2.
Now, where were we? Oh, yes—we were attempting to find a general rule, using the dot product, to find the component of one vector along any other vector—even if it is not of unit length. To do this, however, remember the argument we made that the smallest error in a component occurs when the component is perpendicular with the error vector (the difference between the vector and its component). Looking back at Figure 3 with our newfound understanding of orthogonality, it should make intuitive sense that this is the case. Since vw and the error vector are orthogonal, there cannot be any amount of vw in the error vector, or vice versa. Moreover, if vw were any smaller or larger, there would have to be some component of vw in the error vector—and thus, the error vector would not be as small as possible.
Knowing this, how do we modify our existing vector equations to account for the non-unit length of vector w? Well, since our ideal component along w forms a right triangle with the error vector and v, we can use simple trigonometry again to show that
![]() . [Equation 5.1]
. [Equation 5.1]
However, what we really want to find is that constant c, that shows us by how much we scale vector w to make vector vw. Substituting into Equation 5.1, we find that
![]() ,
[Equation 5.2]
,
[Equation 5.2]
and multiplying both sides by |w|,
![]() . [Equation 5.3]
. [Equation 5.3]
So finally, substituting into Equation 5.3 according to the dot product formulas found in Equation 1.1 and Equation 1.2,
![]() .
[Equation 5.4]
.
[Equation 5.4]
We’ve gone through a lot of work to get to this formula but you can see that it represents the constant c in a very understandable way. The dot product in the numerator is basically the same simple trigonometry operation we performed in Equation 5.1—the projection of one vector on another. The dot product in the denominator is responsible for normalizing c, in the case when our basis vector is not of unit length. This equality will work when attempting to find by how much you would scale any vector w to make it the perfect component—the best approximation—of any other vector v. Now, we are finally ready to delve into the world of signals, armed with our vector knowledge. We will find that there are countless similarities between what we have learned in the realm of vector construction, and the practice of building signals from their components.
The Dot Product: Strong Enough for a Vector, But pH Balanced for a Signal
Up to this point, it may seem to you as though we’ve gone a little out of our way in our discussion of signal analysis—you’ve been led through a winding discussion of vector mathematics, a great deal of which you probably already know. However, have faith—this journey has been truly worthwhile, because there is an amazing parallel between what we have done so far with vectors, and what we are about to do with signals. As Lathi powerfully states it, “the analogy is so strong that the term ‘analogy’ understates the reality. Signals are not just like vectors. Signals are vectors!”
What does this mean? Just as we can break down vectors into a sum of components, given some arbitrary basis set, we can break down signals into a sum of components, according to a set of basis signals. But wait, there’s more! Just as we were able to define a vector dot product, and use it to find vector components, we can determine an analogous signal dot product. And perhaps, we can use it for the same noble purpose—breaking down signals into their components.
For any two real signals a(t) and b(t), the dot product of the signals over the interval [t1, t2] is
![]() . [Equation 6]
. [Equation 6]
Like its vector counterpart, the dot product in Equation 6 is a way of measuring of the “relatedness” of two signals. As a result—just like the vector dot product—we can make assumptions about the relationship between the two signals a(t) and b(t), given the sign of their dot product. Although we will discuss this more in the section on correlation, a positive dot product means that two signals have a lot in common—they are related in a way very similar to two vectors pointing in the same direction. Likewise, a negative dot product means that the signals are related in a negative way, much like vectors pointing in opposing directions.
Problem 3: What does the dot product of a signal with
itself tell us about that signal? How
does this correspond to what we have learned about vectors? [8 pts.]
Perhaps the most interesting point is that we can also draw assumptions about two signals whose dot product is zero. Just as in the world of vectors, the two signals whose dot product is zero are orthogonal—and thus, like vectors, are completely unrelated and cannot be formed from one another. Hence, two real signals a(t) and b(t)are orthogonal over the interval [t1, t2] if
![]() . [Equation
7]
. [Equation
7]
We will examine signal orthogonality further in the next section. But wait, the vector-signal analogy does not stop there, either! Just as with vectors, we can use the signal dot product to find the component functions of signals. Let’s assume we have two signals, f(t) and g(t). Now, let’s consider g(t) to be a basis function, which we can use to construct other signals. As you may imagine, in constructing the signal f(t) from components, we will need a complete set of basis functions may include g(t) (as well as many others). Take a look back at Figure 3, and remember how we constructed the component of vector v. It would follow from our vector-signal analogy that for our signals f(t) and g(t), there exists some constant c such that
![]() . [Equation
8]
. [Equation
8]
Once again, we can think of this situation as using g(t) to approximate the signal f(t) over some interval. And, just as we did with the vectors, we want to be able to find a value for c that minimizes the error in our approximation. However, since we are working with signals, instead of measuring the error in terms of magnitude, it is far more appropriate to quantify our error in terms of signal energy (a measurement with which you should be familiar). Fortunately, it is the case—Lathi derives this result well in Section 3.1-2—that as with vectors, our minimal error occurs when
![]() . [Equation
9.1]
. [Equation
9.1]
And thus, the exact value of c, over the interval [t1, t2], is given by
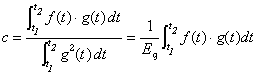 , [Equation
9.2]
, [Equation
9.2]
where Eg is the energy of the basis signal g(t). Now, let’s see if we can put these equations to work obtaining the components of a signal.
Problem 4: The
figure below shows a signal f (t), along with three basis functions, g1(t), g2(t), and g3(t),
represented over the interval [0,T], where A = 2 and
T = 3. Take the dot product
of f (t) with each basis function—what do your results tell us about the
relationship of f (t) with each function? Which of the three would be the best basis
function to use in beginning to build f
(t)? Explain.
Using this “most desirable” function, find the value of c, the amount by which the basis
function should be scaled to make it a component of f (t). Sketch or graph the error signal, e (t). Can this error be reduced using only the one
basis function you chose? [12 pts.]
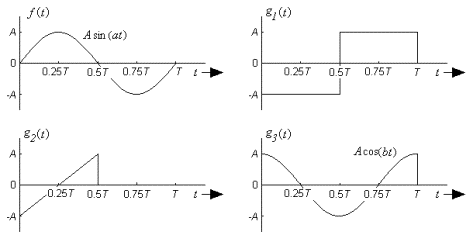
Figure 5: Signal and basis functions for Problem 4.
Signal Correlation: Lathi’s “Best Friends, Worst Enemies, and Complete Strangers”
We have now approached the point where we can begin to use what we’ve learned about signal construction to perform some very useful operations. One of these valuable calculations is correlation—a measure of the similarity between signals. And as you may guess, the computation of two signals’ correlation is based on our new friend the signal dot product.
Let’s begin by taking a look back at vectors. We have already stated the dot product can be seen as a measure of the “relatedness” of two vectors. However, this measure is not absolute, since the size of the dot product depends not only on the angle between the two vectors, but also their individual magnitudes. And, if we define “similarity” in a vector sense to mean simply direction, then our measure of correlation should be independent of the magnitudes of the vectors involved. So, to compensate for magnitude, we just divide by the lengths of the vectors—normalizing the dot product, so that we can examine only directional similarity. The similarity of direction cn between two vectors a and b, with an angle of q between them, would then be
![]() . [Equation
10]
. [Equation
10]
So, to measure how correlated two vectors are, all we need is the cosine of the angle between them. Consequently, cn—which is called the correlation coefficient—always ranges from –1 to 1, regardless of the size of the vectors measured. A correlation of cn = 1 corresponds to two vectors that are as similar as possible—thus, they must be positively scaled versions of one another (since the angle between them is zero). Likewise, a correlation of cn = –1 corresponds to two vectors that are oppositely similar (since they have an angle of 180º between them). Finally, vectors with a correlation of zero are, as before, orthogonal—they have nothing to do with one another.
How does this relate to signals? Just as with vectors, we should be able to “divide out” the sizes of the two signals from the signal dot product, leaving us with a measure of pure similarity. To accomplish this, we have to compensate for our measure of signal size—that is, we have to normalize the two signals to unit energy. So, if we consider the entire range of (-∞,∞) then the correlation between and two real signals a(t) and b(t) is
![]() , [Equation
11]
, [Equation
11]
where Ea and Eb are the respective signal energies of a(t) and b(t). Observe that as before, cn is independent of the energies of our signals, ranging always from –1 to 1.
So how do we interpret signal correlation? Well, if the correlation between two signals is cn = 1, then as with vectors, the signals are simply scaled versions of one another. Barring signal energy, the two signals are as similar in shape as they could possibly be. And, as with vectors, a correlation of cn = –1 signifies two signals which are also identical in shape, with the important exception that one is the negative of the other. Finally, two signals that have no correlation (cn = 0) are orthogonal. Orthogonal signals cannot be components of one another. Here is another way to think about it: if we were to use a signal g(t) to approximate another signal f(t), and f(t) and g(t) were orthogonal, then the minimum error that we could achieve is if we used none of g(t). Adding or subtracting even the least little bit of g(t) to or from f(t) would only serve to increase the error in our approximation.
Problem 5: The figure below shows a function x(t), along with five other functions: y1(t), y2(t), y3(t), y4(t), and y5(t). For A = 3, b = 2, and T = 4, state whether x (t) is positively correlated with, negatively correlated with, or orthogonal to each of the other five functions. (It may not be necessary to perform the dot product integral in every case; you are free to combine mathematical and graphical arguments.) [15 pts.]

Figure 6: Signals for Problem 5.
As Lathi phrases it in Section 3.2, the three different instances of signal correlation where cn = 1, –1, or 0 are like the relationships between “best friends, worst enemies and total strangers”. To clarify: positively correlated signals are related in the way of a friendship, whereas negatively correlated signals have an association akin to that of enemies—very similar in essence, except in opposing ways. Orthogonal signals, however, are truly like “complete strangers”. They possess a quality that would compare to being, in the words of Lathi, “of different species or from different planets”.
On a side note, correlation itself is actually much more than just another mathematical avenue for us to travel on our route to signal construction. Correlation calculations are used in a number of applications—for instance, in signal detection applications. One example of this, with which you are probably familiar, is radar (radio detection and ranging). In radar, a pulse shape is transmitted via radio waves into the open air, where any object that we would want to detect may be located. Although the receiver usually reads only noise from the environment, if an object does enter the detection space, then the signal is reflected back. There is at least one major problem with this approach, though: how does the receiver identify the reflection of the transmitted pulse, amongst all of the noise? One solution is to use correlation—we can quantify the extent to which the signal we received resembles the signal we sent. Then, we can make a decision about whether or not an object has been detected, based on this correlation value. The thing that makes correlation particularly well suited for this purpose is that it doesn’t care about the size of the pulses. Thus, we can evaluate how closely the shape of the reflected pulse matches the transmitted pulse, even though it has been heavily attenuated by propagation through the air.
Part 2: The
Building Blocks of Signals
How Do I Get My Very Own Orthonormal Basis
Set?
Before we can answer that question, we need to consider: what is an orthonormal basis set? Most obviously, it is a set that we may use as a basis—that is, a collection of vectors (for constructing vectors) or functions (for constructing signals) that we can use as basic building elements. What truly defines a basis set, however, is that there are enough elements in the set that when they are scaled properly and added together, they can perfectly build any vector or signal. An orthonormal basis, though, is a little more than just another basis. Perhaps the best way to attack this subject is by deconstructing and analyzing the term itself.
So, let’s begin—the first part of the term “orthonormal basis” is ortho-, as in orthogonal. What does this part tell us? It tells us that in order to break down accurately vectors or signals into their components with a single dot product calculation per component, the components need to be orthogonal. This is a lesson we learned back in Problem 2—if our components are even slightly made up of one another, then it becomes far more difficult to discern how much of each element we need. This is because we have to consider the relationship—the correlation—between our basis vectors or functions. Of course, we know for orthogonal elements that this relationship does not exist; they are, as we said before, “strangers”. Thus, we can examine the component of a vector or signal along each basis element individually.
The next part of the term to consider is -normal. We discovered very early on in this discussion the convenience of having our basis elements normalized. This does not even necessarily mean that the basis vectors have to be of unit length, just that your basis vectors are all at least the same length. Another way to think about it is: if you have a two-dimensional displacement vector, it would be ridiculous to break it down into a component measured in feet, and another measured in meters. The two values would have no meaning with respect to each other, without performing some kind of a unit conversion—such a basis would be inconvenient. In signal construction terms, this means that normalization allows us to compare the size of the component functions with each other, without having to perform extra calculations.
Finally, as we said before, our orthonormal basis set must truly be a basis for its intended vector or signal space. No matter how many vectors or functions the basis set includes, there has to be enough such that we can completely build any vector or signal that could exist in the space. Consequently, for two-dimensional or three-dimensional vectors, we need two or three basis vectors in the set, respectively. (Of course, all of the basis vectors must be linearly independent—they cannot be scaled versions of one another, or we wouldn’t really have different vectors.) For signals, however, this usually means that we need an infinite number of orthogonal basis functions.
The necessity for an infinite basis set makes the other two characteristics—orthogonality and normalization—even more important. Just imagine if our infinite set of functions was not orthogonal. We would have to take into account the correlation between infinite pairs of signals—this would be impossible! Or, imagine if our basis set was not normalized—we would have to keep track of the infinite series of coefficients that told us how the signal energy of each basis function differed from every other. That sounds a little difficult as well, does it not?
Problem 6: Consider the three qualifications a set must possess to be considered an orthonormal basis. In terms of its usefulness in representing signals as their components, which would you consider to be the most important qualification, and why? Which would you consider to be the least important, and why? [12 pts.]
So, let’s recap—an orthonormal basis is a very useful set of elements that possesses three main characteristics. First, all of the elements need to be orthogonal, so we can calculate the projections of our signal or vector on each basis element individually. Second, all of the elements should be normalized, so that we don’t have to concern ourselves with a different size factor for each element, and we can easily compare the components to one another. Finally, the set should form a complete basis, from which we can construct any vector or signal we could imagine within the given space.
Fun with Walsh Functions
One well-known orthonormal basis is the set of Walsh functions. As a basis, these functions can be used to construct any continuous signal within the finite range of time over which they are defined. The function values are actually obtained from the rows of a special matrix known as the Hadamard matrix. If it interests you, feel free to further investigate the origins of this fascinating collection of functions.
Walsh functions have a number of unique qualities. First of all, the Walsh functions have the same characteristics that are possessed by any orthonormal basis set for signals; namely, there is an infinite number of them, they are all mutually orthogonal, and they are all normalized to the same signal energy. One of the more unusual characteristics of the set of Walsh functions is that they take on only two amplitude values (usually 1 and –1). This means that they can be generated rather inexpensively and efficiently using basic logic circuits, such as inverters—and more importantly, it is possible to implement the multiplication of a Walsh function by a signal, simply by inverting the signal over the correct intervals. The following problem examines some more of the Walsh functions’ characteristics.
Problem 7: The figure below shows the first eight
elements in the infinite set of Walsh functions. First, notice the Walsh function w1(t)—if we
use these Walsh functions to create a signal, what “frequency” does w1(t) represent? From looking
at the graphs, can you derive a general rule for how the Walsh functions have
been ordered? Which Walsh functions are
even (about the center of the interval, t = 0.5)? Which are odd? If the Walsh functions are to be a complete orthonormal basis
set, can you explain why it is necessary to have both even and odd types
of components? [8 pts.]

Figure 7: First eight Walsh functions over the interval [0,1].
Problem 8: Consider the continuous-time signal
![]() [Equation
12]
[Equation
12]
over the interval [0,1]. With respect to the center of the interval, is this signal even, odd, or neither? Of the first eight Walsh functions (shown in Figure 7), which ones form nonzero components of x (t)?
What kind of difficulties will we encounter if we try to represent x (t) accurately with a limited number of Walsh function components? How might a different basis allow us to improve upon these difficulties?
Using the set of Walsh functions as an orthonormal basis, write a Matlab m-file that can find the components of the signal x(t), and reconstruct it over the interval [0,1]. To accomplish this feat, you are going to need to review everything you have learned so far about what an orthonormal basis set is, and how to find out how much of each basis function is needed. Also, since an infinite number of components are needed to reproduce x (t) exactly, the actual reproduction will be an approximation using a finite number of terms. Thus, your m-file should allow you to specify any number of Walsh functions as an input. Before you start, be sure to carefully review the project—come up with a sensible algorithm, in words, for accomplishing this task, and write this algorithm out before you begin to work in Matlab.
Some helpful hints: Matlab can simulate continuous integration by performing a numerical analysis of trapezoidal integration, using the function trapz (look it up in Matlab help for instructions). Also, to generate the Walsh functions, you can use the Matlab function walsh(t,n). For the function arguments, t is an array of the range of points over which the Walsh function is represented (identical to the kind of array you must create to graph any function), and n is the index of the Walsh function. (Note: this function was created specifically for this project, so if you are using Matlab at home, you’ll need to download it off the course web page.)
Also, don’t forget to use the element-by-element multiplication (.*) and power (.^) operators, when multiplying two arrays or raising an array to a scalar power, respectively.
To
document your results: plot x(t), along with its reconstruction using
the first n Walsh functions, for n = 2, 8, 16 and 32. Print each graph—be sure they are titled,
and the axes and curves are appropriately labeled (you can write labels in, or
use the appropriate Matlab commands).
Also, be sure to provide the original algorithm you developed before you
started coding, and be sure to print out your m-file code and clearly state
what each part of your program does (you will want to use the comment operator
(%),
to put remarks in your m‑file).
It is your responsibility to do a good job documenting your algorithm,
code, and graphs, since it is the only way to prove that the work you submit is
indeed your own. [20 pts.]
Written by Nicholas Arcolano — 21 July 1999.
Revised 21 December 1999; 14 November 2000;
28 March 2001