Sample Quiz #6

MA 2071

Diagonalization

Solutions in color

 

 

1.      a. What is the definition of eigenvector of a linear transformation? 

 

             x is an eigenvector of L if L(x) =  kx    for some scalar  k  

                         (I'd use lambda but the browsers will probably wreck it, so k)

 

         b. For the  linear transformation  L(y) = d²y/dx²    which of the following are eigenvectors? For those that are, what is their eigenvalue??

 

                     i) y = e^3x            ii)  y  = x³          iii)    y = cos(5x)           iv)    y = ln(x)

 

               yes, L(e^3x) = 9e^3x           no                         yes;  -25                             no

               eigenvalue of 9

 

 

2.    For the given matrix, find its eigenvalues and an eigenvector for each 

                                                              

 

         

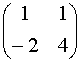
            characteristic equation for this matrix  is  k² – 5k + 6 = 0   with roots of  2 and  3

           for eigenvalue of 2:  eigenvector is any multiple of  ( 1  1)

           for eigenvalue of 3:  eigenvector is any multiple of   (1 2)

 

 

3.   For a given eigenvalue of a matrix,  why is the corresponding eigenvector not unique?   Feel free to use your work from Problem #2  to illustrate the point.

 

            eigenvectors are solutions of homogeneous systems so there are arbitrary variables involved; any choice

            of the arbitrary variable results in a solution. In problem 2, for eigenvalue 2,  perfectly good answers

            would also be  (2,2),  (3,3),   (10,10)  etc etc

 

            In matrix terms, a proof would look like:

 

                   if  x is an eigenvector for eigenvalue k  then  cx is also an eigenvector for any scalar c

                          proof:

                                     Ax = kx  by definition of eigenvector

                                     A(cx) = cAx  since matrix multiplication is linear

                                               = c(kx)  since x is an eigenvector

                                               =  k(cx)  since ordinary number multiplication is commutative

                                   therefore  cx  is an eigenvector for eigenvalue of k .

 

 

4.    The following matrix has eigenvalues computed to be   1,1  and  4(note correction from earlier versison which had a 1 in the  3,3 entry)

                                               

      

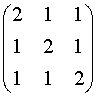
        a)  diagonalize it

 

                        you need a basis of eigenvectors  so

                                     for k = 4 you should get  (1  1  1)  or any multiple

                                     for k = 1   you should get two solutions,  (-1  1  0)   and  (-1  0  1)

                       Now you can set up the matrices:

 

                                A = P D P^-1

 

                               or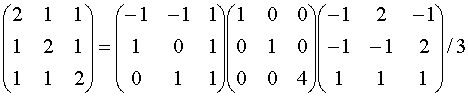    

 

 

                        ( I factored a 1/3 out of all the terms in the last matrix, P^-1)

                        note this is not the only solution. You could order your eigenvectors differently or use different

                        eigenvectors and be perfectly correct. 

                                              

 

        b)  use your result in part a)  to find   the 2^nd and 5^th  and powers of it

 

 

            any power, k, of the matrix A would be given by

 

 

                       

 

       

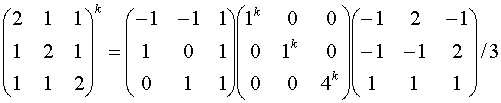
            c)  what is the determinant of A based upon your Diagonalization?? (this is easy! use things you've learned about determinants)

 

 

                       Det(A) = Det(P D P^-1)

                                    =  Det(P) Det(D) Det(P^-1)   by product rule for determinants

                                    =  Det(D)           since Det(P^-1) = 1/Det(P)

                                    = 1*1*4              since D is diagonal

                                    = 4

 

        d)  What is the inverse of A based upon your Diagonalization ?

 

                        A^-1 =  (P D P^-1)^-1

                              =  P D^-1 P^-1    by rules for inverses from earlier in the course (specifically that

                                                     (AB)^-1 = B^-1A^-1   in case you're wondering )

                        but D is diagonal so its inverse is easy to find and we end up with

 

 

                       

 

 

 

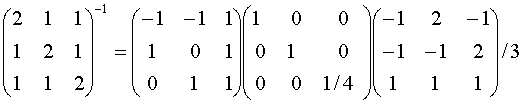
            or, more significantly, all you have to do is invert the diagonal entries, which are simply numbers!

 

 

 

5.  Prove that the eigenvalues of an upper triangular matrix are the entries on the diagonal of it  (OK to use a

3x3 for purposes of a proof).

 

 

            if  A is upper  triangular  then  the characteristic equation

 

                        Det (A – kI_n)=0  is the determinant of another upper triangular matrix  (subtracting k down the

                        diagonal does not change that) and we know that the  determinant of an upper triangular matrix

                        is the product of the diagonal entries. So…. in the 3x3 case the determinant would look like

 

                                    Det(A – kI₃) =  (a₁₁ – k) (a₂₂ – k) (a₃₃ – k)  =   0

 

                        which is all nicely factored and thus has roots of  a₁₁, a₂₂  and a₃₃.

 

            the upshot is: if your matrix is upper (or lower) triangular then all you have to do is look at it to get

                        the eigenvalues!  For example, the eigenvalues of

 

 

                                   

 

                        are 1, 2 and 4. No work needed. 

 

 

 

6.   Prove:  if A has no inverse then 0 is an eigenvalue of A

 

                        if A has no inverse, we know its determinant is 0 or  Det(A) = 0 

                        Thus

 

                                    Det(A – 0I_n) = Det(A) = 0    so 0 satisfies the equation and is thus

                        an eigenvalue.

 

                        (in this case, the constant term in the characteristic equation would be 0)