FRACTALS

FRACTALS

*What is a Fractal?

A Geometric pattern that is repeated at ever smaller scales to produce irregular shapes and surfaces that cannot be represented by classical geometry.

Fractals are used especially in computer modeling of irregular patterns and structures in nature.

[French from Latin frctus, past participle of frangere, to break.]

The Sierpinski Triangle- every triangle is divided into four, with the

center being taken out. This keeps going, making it a fractal.

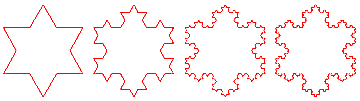
The different steps in making the Koch Snowflake

What are fractals used for?

In our project we learned how to use fractals as a form of image compression. We all made our own fractals by choosing a Julia Set or an, using z as a complex number and c as a constant.

Jenn's Fractal- 0.5 z²-c http://www.wpi.edu/~goulet/jen.JPG

Tony's Fractal- z⁴+c http://www.wpi.edu/~goulet/tony.JPG

Isabel's Fractal- z³-z²+c http://www.wpi.edu/~goulet/isabel.JPG

Chuck's Fractal- z³+c http://www.wpi.edu/~goulet/chuck.JPG

We also learned how to figure out fractal dimensions using the formula log(parts kept) \ log(total sides)

In the above, Koch Snowflake, the dimension is 1.26

log(4) / log (3)