Solutions

Geometry

Problem Set #6

Here we wish to put everything together covered so far. For each equation listed,

a) put it in Standard Form for a parabola

b) identify its vertex

c) decide if it opens up or down

d) find the value for d and determine where it’s Focus is

e) use algebra to find where it intersects the x axis or show that it does not

f) sketch it by hand, incorporating all of the information found in parts a) – e)

1. 32y + (x-4)² = 64

a) Standard Form : b) Vertex: (-4,2) c) down d) d=8

e) y=0 => (x+4)² = 64 => x+4 = +/-8 => x = -4 , -12

2. 8y + x² = -16

a) Standard Form : b) Vertex: (0, -2) c) up d) d=2

e) y=0 => (x)² = 16 => x = +/-4

3. y -x² -8x = 0

a) Standard Form : y+16 = (x+4)² b) Vertex: (-4,-16) c) up d) d=1/4

e) y=0 => (x+4)² = 16 => x+4 = +/-4 => x = 0,8

4. 16 y + x² -20x -4 = 0

a) Standard Form : 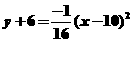b) Vertex: (10,-6) c) down d) d=4

e) y=0 => (x-10)² = -96 => no solution so no intersection with x axis (vertex below x axis, opens down)

5. y = x² +14x + 40

a) Standard Form : y+9 = (x+7)² b) Vertex: (-7,-9) c) up d) d=1/4

e) y=0 => (x+7)² = 9 => x+7 = +/-3 => x = -10,-4

6. y = x² - 25

a) Standard Form : y+25 = x² b) Vertex: (0,-25) c) up d) d=1/4

e) y=0 => x² = 25 => x = +/-5