Functions

Contents:

1. Basic definition

2. Notation

3. Graphing Functions

Basics

Even and Odd Functions

Vertical Line Test

4. Piecewise Functions

5. Absolute Value Functions

6. Greatest Integer Function

7. Inverse Functions

Horizontal Line Test

8. Composition of Functions

9. Notational Problems Frequently Encountered

1. Basic definition

A function takes quantities and transforms them into other quantities. That’s our starting point. The objects it begins with, collectively, are called it’s domain. The results of all the transformations are it’s range.

Kind of vague so far. We will try and relate it to everyday life as well as your calculator. On any calculator is a key which looks like x². This means, of course , that whatever number you provide then gets squared. So this corresponds to a function, f, usually denoted as

f(x) = x²

This is read as meaning that f takes x and squares it. So f(2) = 2² = 4. f(-6) = (-6)² = 36.

This function works for any real number x so its domain is all real numbers. The results of this are always positive (or 0) so the range is all non-negative real numbers.

Engineers might think of the domain as inputs while the range is outputs. Sometimes you can think of it as a black box that takes a number and converts it somehow into another number:

Any computer has a power supply. It takes wall current as its domain, which may be anywhere from 90 to 120 volts or more, and converts it into 6 volts DC for use by the computer components. How it does this is fairly complex but viewing it as a function is fairly simple: f(x) = 6 for 90 < x < 120 .

We might have a device for reading temperature. It takes voltages, which vary as resistance varies, and produces a numerical value on a digital readout. The domain might be voltages between 2 and 18 volts DC while the range might be 75 to 110 degrees.

Now anyone would only want one possible temperature associated with a given voltage (this would be checked during calibration for accuracy). This is always the requirement and is formally stated as follows:

For a transformation to be a function, for each item in the domain (input) there can only be one entity (output) in the range.

We could never have two different temperature readings for the same conditions.

As an example, suppose the following data points were gathered for some transformation:

{ (2,1), (3,4), (4,-2), (5,3), (3,6), (6,2), (7,2) }

then this would not be data from a function. Why not? Included in the set are (3,4) and (3,6). These mean that for the input of 3, there are two outputs or values, 4 and 6. This cannot happen if we have a function. For every input there can only be one output.

On the other hand you might be wondering it the pairs (6,2) and (7,2) are a problem. These mean that the inputs of 6 and 7 produced the same output, 2. This is OK. In fact a function which was constant (horizontal line graph) produces the same output for all inputs.

Problem Set 1

1. Each set of ordered pairs comes from a mapping. Decide (yes or no) if the mapping could be a function or not.

a) { (2,1), (3,4), (4,-2), (5,3), (6,3), (7,2), (8,2) }

b) { (1,1), (3,1), (4,-2), (1,3), (7,6), (6,7), (0,2) }

c) { (2,1), (3,1), (4,1), (5,1), (6,1), (7,1), (8,1), (9,1), (10,1) }

2. For each part in Problem 1 that was a function, specify its domain and range

Follow this link for solutions to Problem Set 1

2. Notation

A rule stated like f(x) = x² or g(x) = 5x + 7 or f(x) = sin(x) tells us how the function specifically works in a mathematical way. The symbol x is a dummy variable to show how the transformation is, in general, done. Any other variable tells the same thing. Thus

f(x) = 5x + 9 f(y) = 5y + 9 and f(z) = 5z + 9

all describe the same function: it takes a number, multiplies it by 5 and adds 9.

Problem If g(x) = 7x² + 1

What are

a) g(y) b) g(z²) c) g(3) d) g(g(x)) ?

Solutions:

a) 7y² + 1 b) 7z⁴ + 1 c) 64

d) 7(7x²+1)² + 1 =343x⁴ + 98x² + 8

Problem What are the domain and range of the function

?

Solution:

We cannot take square roots of negative numbers so x has to be 5 or bigger.

The square root results in quantities 0 or greater so adding 7 results in numbers 7 or bigger. Thus

domain: all real numbers ≥ 5

range: all real numbers ≥ 7

Problem for the function f(x) = x³ what is the expression for f(x + h) ?

Solution: start by reading the function carefully. Whatever is given to it as input gets cubed. So in this case we must take x+h and cube it:

f(x+h) = (x+h)³ = x³ + 3x²h+3xh² + h³

An incorrect but frequently given answer is f(x+h) = x³ + h³. This is just playing with symbols.

Problem Set 2

For the given function, determine each of the quantities stated next to it

a) f(x) = 5x² + 7x + 1 f(y); f(x + a); f( f(x) )

b) f(z) = z³ + 1 f(x); f( z + h); f(1/x);

c) f(x) = 2 f(x+h); f(z) ; f(3);

d) f(x) = 1/x f(2+h); f(3/2); f(1/y);

2. For each function below, state what it’s domain and range are

a) f(x) = |x| + 2

b) f(x) = 3 sin(x)

c) f(x) =

d) f(x) = x² + 4

Follow this link for solutions to Problem Set 2

3. Graphing Functions

Basics Assuming one is familiar with Cartesian Coordinates, which are of the form (x,y) where x is the horizontal value and y the vertical value, functions are plotted by setting y = f(x). So the vertical value of a point is the value of the function at the point; in other words, the graph of a function is the set of all (x, f(x)) where x is in the domain of f.

The function f(x) = x³ + 9x² + 3 produces a graph like:

Notice, for example, where it crosses the y axis. That point would be (0,3) because, as we can easily compute, f(0) = 0³ + 9 (0)² + 3 = 3 .

Note that the graph has one high spot and one low spot. These are of great interest in Calculus I and are called local maximum and local minimum, respectively. Also the graph is cupped downward on the left and upward on the right. This is studied in Calculus I with second derivatives and referred to as concavity.

Even and Odd Functions

For example if f(x) = x² + 1 then the graph of f is a parabola opening up with vertex at (0,1):

This is an example of a symmetric graph and therefore a symmetric function. This is shown algebraically by the fact that f(- x) = f(x) for all x because f(-x) = (-x)² + 1 = x²+1 = f(x). Some calculus books also call this an even function. The main thing to remember is that it (an even function) goes hand in hand with a graph which is symmetric with respect to the y axis.

Similarly, if f(-x) = -f(x) then the graph is said to be symmetric about the origin and the function is called odd. The easiest example is f(x) = x³ because (-x)³ = -x³.

The graph of f(x) = x³ looks like

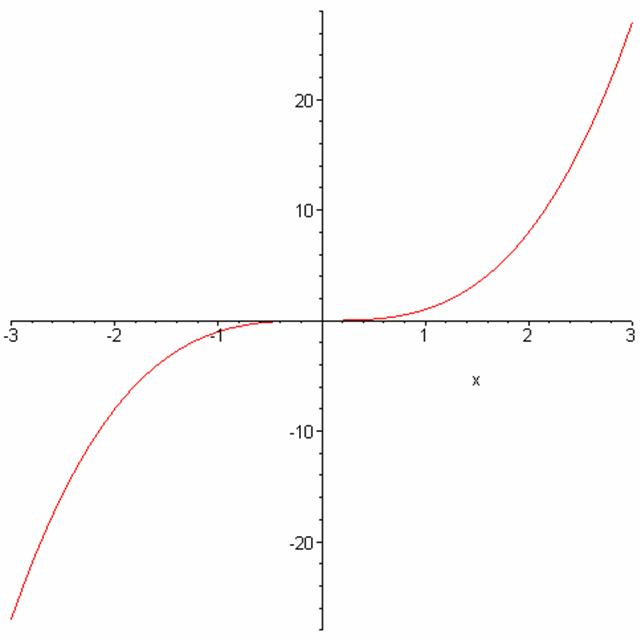
This helps us to perhaps explain the part about “symmetric with respect to the origin”. If you take the right hand side of the graph, reflect it about the y axis and then again about the x axis, you get the other half of the graph.

In Calculus II, which is integral calculus, knowing if a function is even or odd can make doing integrals very easy in certain problems.

In summary,

f is even if f(-x) = f(x) for all x in its domain

f is odd if f(-x) = -f(x) for all x in its domain

with examples of each kind being

even: 1,x², x⁴, x⁶, and cos(x) or any multiples of them

odd: x, x³, x⁵, sin(x) and tan(x) or any multiples of them

(the trig functions depending on identities from trigonometry

sin(-θ) = - sin(θ) and cos(-θ)=cos(θ) ).

If you are thinking that “even” and “odd” has something to do with the exponents being even or odd, you are absolutely correct!

Furthermore, it is easy to show that

a) the sum of two even functions is also even

b) the sum of two odd functions is also odd

c) the product of two even functions is even

d) the product of two odd functions is even

so that

x⁴ + 2x² + 6 is even

x² cos(x) is even

x³ cos(x) is odd

5x⁷ + 4sin(x) is odd

while some functions are neither even nor odd

x⁴ + 6x + 1

cos(x) + x⁵

x³ + 1

ln(x)

10^x

(although it is true that any function can be written as the sum of an even and an odd function).

Problem Set 3

Determine if each function below is even, odd or neither.

1. x⁴ + 6x² + 1

2. x cos(x) + x³

3. 1/x

4. 3x + 9

5. sin(x²)

6. x³ + 1

7. sin³(x)

8. sin²(x²) + x² + 1

Follow this link for solutions to Problem Set #3

The Vertical Line Test for Functions

Discussion: suppose the image below is the graph of a transformation.

This cannot be the graph of a function. Why? For values of x associated with the graph near that point A as well as the point B, there are more than one y value. In fact there are 3 y values for each x in those areas. This violates the definition of a function.

In general, if any vertical lines intersect a graph more than once, you do not have a function. This is called the Vertical Line Test. The graph below would not pass the test either and could not represent a function:

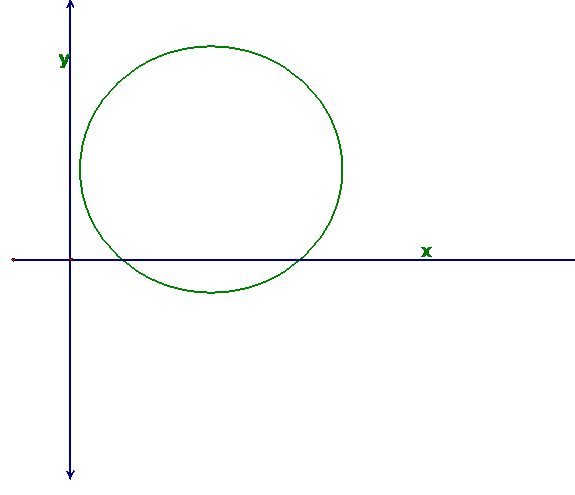
4. Piecewise Functions

Suppose we have the following definition of a function f:

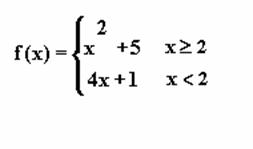
This is called a piecewise definition. You read it as follows:

f(x) = x² + 5 if x is greater than 2 or equal to 2

f(x) = 4x + 1 if x is less than 2

It is still a function, just not quite as simply defined by a single equation. When x is 2 or greater, it has one definition; when x is less than 2 it has a different one. Depending on what x is, you proceed accordingly as shown below:

f(5) = 5² + 5 = 30

f(1) = 4(1) + 1 = 5

f(-2) = 4(-2) + 1 = -7

f(2) = 2² + 5 = 9

Its graph looks like a straight line for x less than 2 and a parabola for x equal to 2 or more.

Problem

if f is defined as

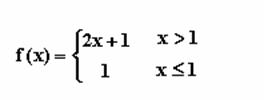
what are the values of

a) f(4) b) f(1) c) f(0) d) f( -1) ??

Solutions

a) 2(4) + 1 = 9 b) 1 c) 1 d) 1

Problem Set 4

1. For each function below, determine the value stated

a) f(x) = x² for x<3 and x+7 otherwise. What is f(4)? f(0)? f(f(0))?

b) f(x) = x if x≥3 and 3 otherwise. What is f(3)? f(10)? f(0)? f(-3)?

c) f(y) = 1 if y≥2 and 2 if y < 2. What is f(2)? f(0)?

d) f(x) = 1 if x is an integer and 2 otherwise. What is f(3)? f(2.2)? f(π)? f(1/2)?

2. if f(x) = x² + 1 when x>1 and -x +3 for all other x, what is the graph of f?

3. if f(x) = x² for x > 3 and 2x + b for all other x, what value of b would cause the graph to be unbroken for all x?

Follow this link for solutions to Problem Set 4

5. Absolute Value Functions

A special case of piecewise functions is the “absolute value function”. For sake of discussion, suppose f(x) = |x| + 1

the vertical lines mean “absolute value”. If x is positive then |x| is just x while if x is negative, then the minus sign is removed. Thus

|-3| = 3 |4| = 4 |9.11| = 9.11 etc

and thus f(-5) = 5+ 1 =6 f(7) = 7+1 = 8 and so on. Not bad so far. Basically it gets rid of the minus sign if there is one.

To define f algebraically requires a little thinking. Because the way f(x) is computed depends on what x is (positive or negative), we really have another one of these piecewise functions. That’s a start. But how do you get rid of a minus sign if x is negative? The answer is: with another minus sign. For example

- (-3) = +3 -(-32.2) = +32.2

So the equivalent piecewise definition of f above would be

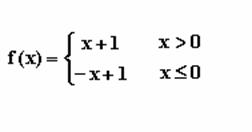
The graph of f is two straight lines:

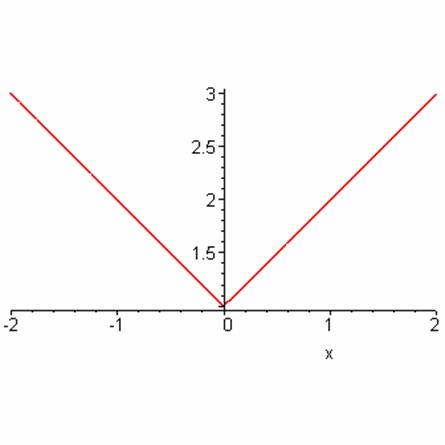
where the lowest point on the graph is x=0, y=1. Lots of the examples of absolute value functions you will encounter in Calculus will have this kind of “V” appearance to them. They bottom out wherever the expression inside the absolute value sign is equal to 0 (x=0 in this case).

Problem: express f(x) = 2|x-5| + 1 as a piecewise defined function.

Solution:

The expression inside the absolute value sign, x-5, changes sign at x=5 so we break up the function accordingly

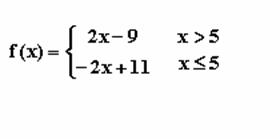
where the -2x+11 comes from 2(-1)(x-5) + 1 = -2x + 11 for x<5

While we are at it , the graph looks like

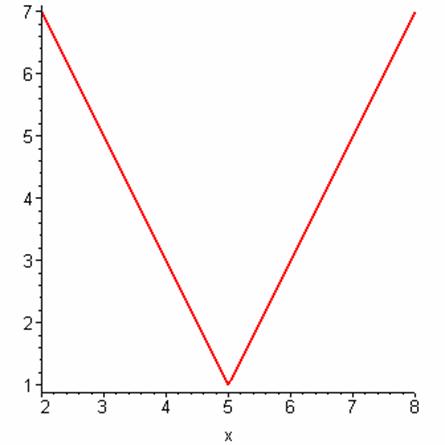
with the low point being at x=5, y = 1.

Problem Set 5

In each case, state the function in a piecewise manner, then graph it

a) f(x) = 3|x-7| + 2

b) f(x) = -|x+4|

c) f(x) = x + |x| + 8

d) g(x) = -|x| + 9

Follow this link to see solutions to Problem Set 5

6. Greatest Integer Function f(x) =

This function looks a lot like an absolute value function. It’s not. Its definition is as follows, and must be carefully read for you to get anywhere with it:

= the greatest integer less than or equal to x.

In computer software, it is often a library function called floor as it effectively rounds down to the next integer.

Looking at examples helps:

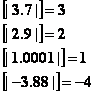
The last one, with a negative number, often gives students problems.

It would appear that

the domain of this function is all real numbers

the range is all integers

The graph is flat in between integers and drops off at each one :

Problems Set #6

1. What are actual numerical values of

a) [| 2.1 |] and [|1.98 |] ?

b) [| -2.1101 |] and [| -1.99|] ?

c) [| π |]

d) ( [| -3.11 |] )² and ( [| 3.11 |] )²

2. What is the domain and range of each function below

a) f(x) = [| x |]

b) f(x) = [| x |]²

c) f(x) = x – [|x|]

3. What is the graph of f(x) = [| x |]² ?

Follow this link to see solutions to Problem Set #6

7. Inverse Functions

OK… we have the basics down. Functions take inputs from the domain, change them in some way and produce outputs in the range. f(x) = x³ takes an x value and changes it into the cube of that number. f(3) = 27.

Sometimes we need to work the other way. Given the output, what input resulted in it?

If f(x) = 64, what was the x value? (4) If f(x) = 125, what input resulted in 125?

If I can have a savings account at 4% interest and I want to have $5000 in it after 4 years with an initial deposit of $800, how much do I have to put in it each month to have that happen?

If the temperature reading of my digital thermometer is 99 degrees, what voltage would have caused that?

The idea of working backwards is called an inverse function. A few numerical problems may help to get the idea planted:

Problem Set 7

1) if f(x) = x² and f(x) = 25, what was x?

2) if f(x) = sin(x) and f(x) = 1, what was x?

3) if f(x) = 2x + 8 and f(x) = 32, what was x?

Follow this link for solutions to Problem Set 7

Notationally, you have to get used to a subtle symbol, a superscript of -1.

This is read as follows (you really need to memorize what follows):

for a given function f, the symbol f^-1(y) means the input that determined y.

This immediately means that if f^-1(y) = x then f(x) = y. This does not look like much but it gives a way to check to see if we are correct. Put differently, a function f and it’s inverse f^-1 must satisfy

f ^-1 (f(x) ) =x

and f( f^-1(y)) = y.

The roles essentially got reversed…we are working backwards.

Let’s suppose f(x) = x³. Then the following are all true

f^-1(8) = 2

f^-1(27) = 3

f^-1(1) = 1

f^-1(-125) = -5

How do we know they are true? We can check one by one using the second requirement above, f( f^-1(y)) = y. For these examples, this amounts to:

f(2) = 2³ = 8 (checks)

f(3) = 3³ = 27

f(1) = 1³ = 1

f(-5) = (-5)³ = -125

and they all check.

Sometimes a calculator is involved. I am trying to determine the cube root of 10. After pressing some keys on my calculator, I get 2.1544 for an answer. How do I know it’s correct? I am working on a project that depends on an accurate number. I think that I have found it but I’d like to be certain. I believe I have found that

f^-1(10) = 2.1544

which is only correct if f(2.1544) = 10. But f(x) = x³ so I take 2.1544 and cube it and find that (2.1544)³ = 9.9995 so, within roundoff limits, my answer of 2.1544 was correct.

Problem Set 8

For each function and inverse value below, determine if that value shown is correct or not:

a) f(x) = 2x+3 f^-1(9) = 3

b) f(x) = x³+3 f^-1(30) = 3

c) f(x) = 8/x + 5 f^-1(9) = 3

d) f(x) = log₁₀(x) f^-1(-2) = .01

e) f(x) = log₁₀(x) f^-1(1000) = 2

Follow this link to see solutions to Problem Set 8.

Not all functions have inverses. The problem is that we want the inverse to be a function as well. This means, if we think back to the original requirement of being a function, that for every entity in the range, there can have been only one entity in the domain corresponding to it. To make this more concrete, let’s look as an example

f(x) = x² + 2

whose graph looks like a parabola with vertex at (0,2)

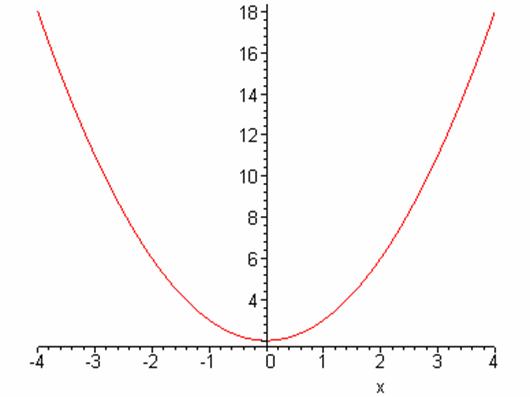
Does this have an inverse function?? If so let’s call it g. Now f(2) = 6 for example, so g(6) should equal 2. No problem so far. But then we also have that f(-2) = 6 so g(6) should also equal -2. This means g is not a function, g(6) can’t be both 2 and -2, which kills things right there.

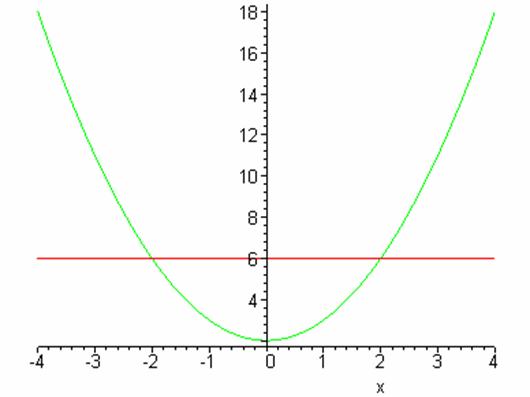
Putting things together: a function f can only have an inverse if for each x in it’s domain there is only 1 y in it’s range (called a “1 to 1” function).

This means that each horizontal line can only intersect the graph of f once. If a horizontal line intersects the graph twice then for that y value there would be two x values and thus it would not be possible to have an inverse function. This is usually called the “horizon line test “ for inverse functions. The vertical line test applied to the function f(x) = x² + 2 might look like

Another function with no inverse based on the view of it’s graph would be

f(x) = x³ + 6x² + 5

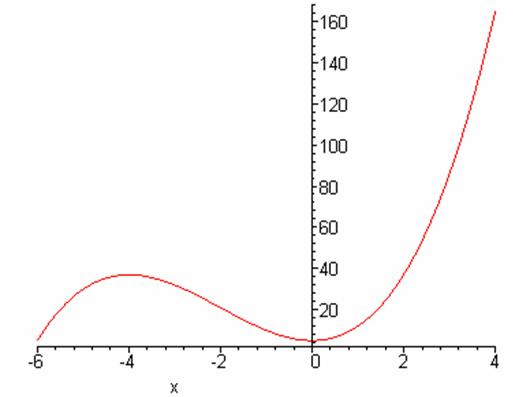
whereas the function f(x) = x³ + 2 does have an inverse as we can see by looking at it’s graph:

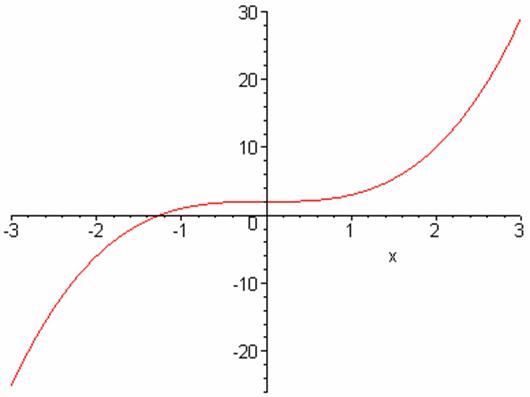
It might look like there is a problem at x=0 but the horizontal line y=2 only hits the graph in one place, the point (0,2). The inverse function here is

g(y) = (y-2)^1/3

How do you find the inverse function?? Assuming it has one, begin with the function

· f(x) and set it equal to y

· Then solve for x in terms of y.

· The expression you get is f^-1(y), the inverse.

For example, the straight line function f(x) = 3x + 5 has an inverse found as follows:

y = 3x + 5

y-5 = 3x

(y – 5)/3 = x = f^-1(y)

We can verify that it really is the inverse as follows:

f^-1( f(x) ) should equal x

Here

f^-1( 3x + 5) ) = (3x + 5 -5) /3 = ((3x)/3 = x.

Problem Set 9

For each function given, decide if it has an inverse and find it’s inverse, for those that do. Verify your result by direct substitution.

a) f(x) = 9x +2

b) f(x) = x³ + 9

c) f(x) = x²

d) f(x) = 5

e) f(x) = 1/(x-5) domain all x except 5.

Follow this link to see solutions to Problem Set 9.

8. Composition

Often it takes more than one function to get the job done, one applied after the other. The fancy name for this is “composition” and it has it’s own notation that you will encounter. The purpose here is to make that concept and notation clear.

For example the function is really a composition. Think of computing a value of it on your scientific calculator. Say you wanted First you would use the sin key to determine the sin(20). Then you would use the to determine the square root of whatever sin(20) had evaluated to. It took 2 functions to get the job done, sine and . Thus this is exactly what we have been talking about, a two step process or a composition.

In concise terms what you did was to evaluate for a specific value of x (20).

This is seen as the composition of the square root function with the sine function, in that order (order is important! ). This is written in calculus books as

where, in this case, f is the square root function and g is the sine function and is read “f composed with g of x “. The small circle above is the key identifier that composition is going on. The following equation formally defines what it means

and says, in effect: for a given x, first find g(x) then use that as input for f.

(For anyone checking the earlier example with their calculator, they should have gotten a final value of about .5848 for with the first number being .3420 for the sin(20) )

Examples

1. If f(x) = 3x² + 4 and g(x) = 5x + 6 then f◦g(x) = f(5x + 6) = 3(5x+6)² + 4

while g◦f(x) = 5( 3x² + 4) + 6

2. if the function is 1/(3x + 7) it may be written as a composition f◦g(x) where g(x) = 3x + 7 and f(x) = 1/x

3. the function cos²(x) + 6 can be written as the composition of x² + 6 with the function cos(x)

Problem Set 10

Write each expression below as the composition of two functions and identify the first as g and the second as f for purposes of answering

1)

2) | x² + 2x + 1| + 7

3) sin³(x) + 1

4) (x² + 2x + 5)² + 1

5) cos(x²)

Write one expression for what is in each case

6) f(x) = 3x² + 1 g(x) = 9x + 1

7) f(x) = 3 g(x) = x⁴

8) f(x) = 3x² g(x) = x⁴

9) f(x) = x|x| + 9 g(x) = 3

10) f(y) = 4y+5 g(z) = 3z²

Follow this link for solutions to Problem Set 10

In Calculus One, you will learn how to differentiate compositions; this is one of the most important skills you will take from that course – it will be called the Chain Rule – and will impact your chance of success in subsequent courses. We are trying to lay the groundwork here.

9. Notational Problems Encountered with functions

Students in calculus sometimes get confused by vague notation used by calculus books and instructors for functions. We will try to examine a couple of them and avoid future problems.

Example 1: a textbook reads sinx What is this? Students sometimes think it means sin times x. It does not. It really means sin(x), the trig function but someone carelessly (and frequently) left out the parentheses which are a part of good function notation.

By the way, sin times x is meaningless. Sine is a function and needs input to have any meaning.

Example 2: a student encounters and is asked to work with it. But what does it mean?

What it does mean is the sin of x , quantity cubed, or

In other words, you start with x, find the sin of it, and take that answer and cube it.

Thus

(the units on x here are being taken as degrees as opposed to radians)

Students sometimes mistakenly assume that sin³x and sinx³ are the same…that you can move that exponent of 3 horizontally somehow and it is ok. Sorry…it’s not!!

An exponent of -1 can be a real problem. It can mean one of two things:

multiplicative inverse (i.e. 2^-1 = ½ tan^-1(x) = 1/tan(x) = cot(x) )

function inverse ( tan^-1(x) = Arctan(x) as opposed to )

and you simply have to carefully read the context of the problem to decide which one you have. There is no nice way out of it!